예제: 힐버트 변환
hilbert 함수를 사용하여 실수 신호의 힐버트 변환을 생성합니다. 이 경우 분석 신호의 이산 푸리에 변환은 음수 주파수에서 크기가 0입니다.
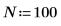
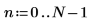
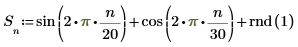
2. 입력 신호를 도표화합니다.
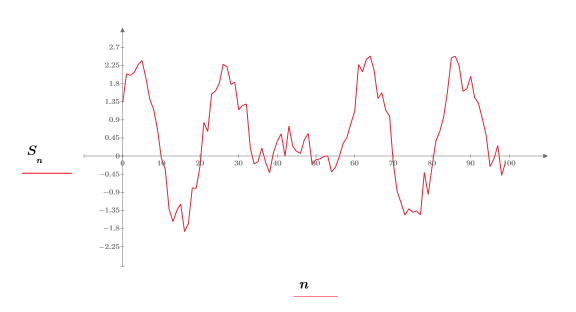
3. hilbert 함수를 사용하여 입력 신호의 힐버트 변환을 계산합니다.
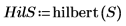
4. 힐버트 변환 신호를 도표화합니다.
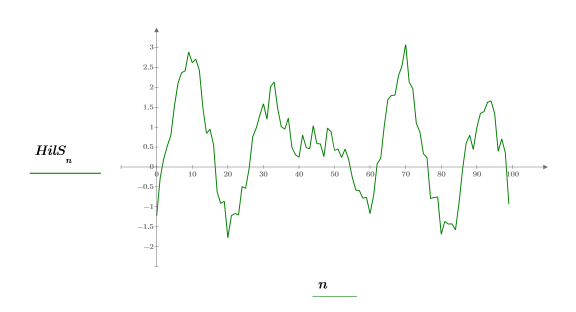
5. 복소 신호를 작성하고 도표화합니다.
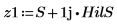
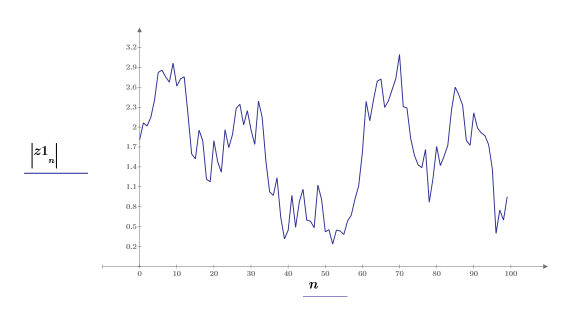
다음 단계는 분석 신호의 크기가 원래 신호의 복소수 포락선임을 보여주는 것입니다.
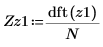
7. 스펙트럼의 절대값을 도표화합니다.
벡터의 경우 dft 함수와 더 이상 사용되지 않는 CFFT 함수 사이의 배율 인수는 1/N입니다.
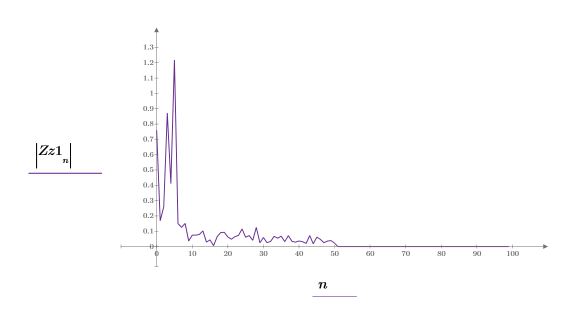
8. 한 그래프에 신호 네 개를 모두 도표화합니다.
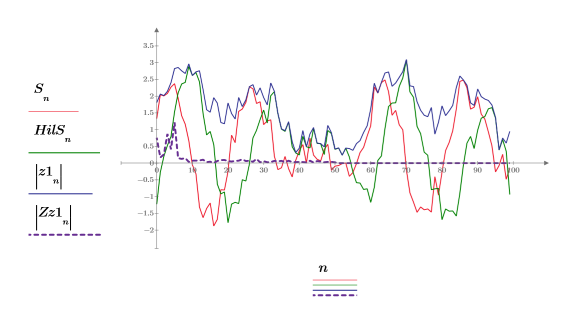
힐버트 변환으로 생성된 새 신호는 변환 영역에서 다음과 같은 방식으로 입력 신호에 상대적입니다.
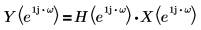
여기서 H를 힐버트 변환기라고 하며, 다음과 같은 주파수 응답의 필터입니다.
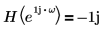 | 다음 조건인 경우 | 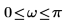 | |
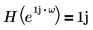 | 다음 조건인 경우 | 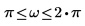 |
필터 설계 프로시저와 함수에서 H를 작성할 수 있습니다.
이상적 힐버트 변환기
이상적 힐버트 변환기에 대한 계수는 Rabiner 및 Gold의 Theory and Application of Digital Signal Processing(Prentice-Hall, Inc.)에 나와 있습니다. 아래 예는 Stearns 및 David의 Signal Processing Algorithms(Prentice-Hall), Section 14.4에 나와 있는 처리 방법에 근거합니다. 이상적 필터의 계수는 홀수 길이 L의 정상 필터를 얻기 위해 창을 씌운 후 이동됩니다.
1. 길이와 중심을 정의합니다.
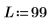
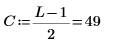
2. 창을 씌우지 않은 계수 h를 정의합니다.
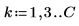 | ||
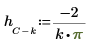 | 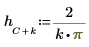 | 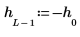 |
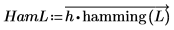
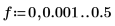
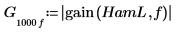
5. 게인과 주파수를 도표화합니다.
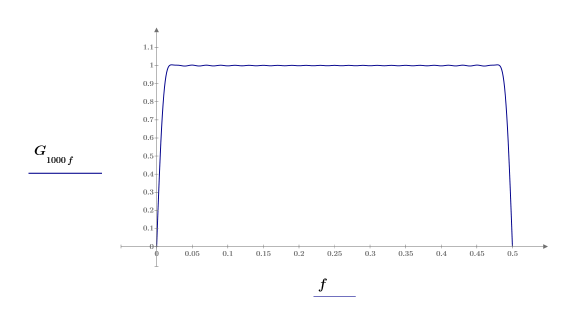
주파수는 표본 주파수 1로 정규화됩니다.
필터는 지연 C를 가지며, 이 지연 신호에 상대적인 필터의 위상 편이를 계산합니다. 지연에 이 전달 함수가 있습니다.
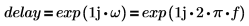 | ||
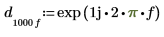 | ||
여기서 | 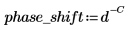 | |
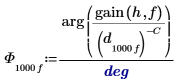 | ||
7. 도 단위로 위상 편이를 도표화합니다.
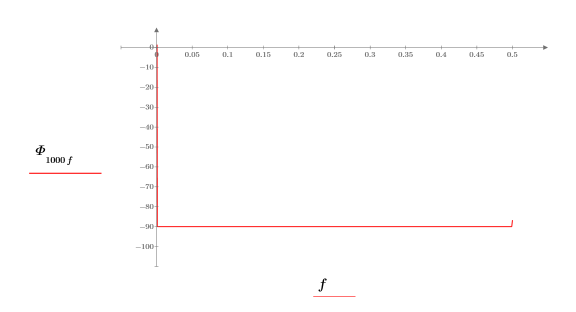
편이는 전체 주파수 범위에서 약 -90도입니다.
필터 테스트
1. 신호 매개변수를 정의합니다.
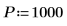
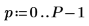
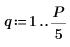
2. exp 함수를 사용하여 새 신호를 생성합니다. rnd 함수는 저주파 노이즈를 추가합니다.
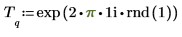
rnd 위로 커서를 이동하고 F5 키를 눌러 다시 계산하여 다양한 난수 신호 T를 얻습니다.
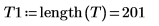
3. 이러한 요소의 공액을 신호의 마지막 200개 위치에 배치하여 신호 반전 시 실수 결과를 얻을 수 있게 만듭니다.
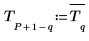
새 벡터에는 1001개 요소가 있으며, 여기서 1~200번 요소에는 원래 벡터 T가 포함되고 801~1000번 요소에는 T의 공액이 포함됩니다. 그 사이의 요소는 0으로 설정됩니다.
4. 신호 T의 푸리에 변환을 구합니다.
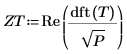
Re 함수를 사용하여 작은 허수 반올림 오차를 제거합니다. 노이즈는 변환 T를 구성하여 생성합니다. 이 변환에서는 처음 요소 다음의 초기 200개 요소에 난수 위상과 단위 크기를 사용합니다.
5. 변환된 신호를 도표화합니다.
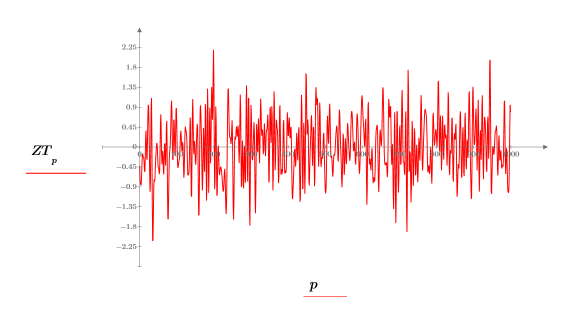
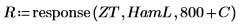
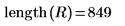
7. ZT의 처음 800개 요소와 R의 마지막 800개 요소를 사용하여 복소수 신호 z2를 작성합니다.
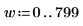
푸리에 변환 벡터 ZT의 처음 800개 요소를 벡터 a2에 저장합니다.
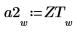
응답 벡터 R의 마지막 800개 요소를 벡터 b2에 저장합니다.
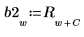
복소수 신호 z2를 정의합니다.
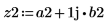
8. dft 함수를 사용하여 신호 z2의 이산 푸리에 변환을 계산합니다.
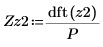
벡터의 경우 dft 함수와 더 이상 사용되지 않는 CFFT 함수 사이의 배율 인수는 1/P입니다.
9. 신호 z2의 이산 푸리에 변환에 대한 절대값을 도표화합니다.
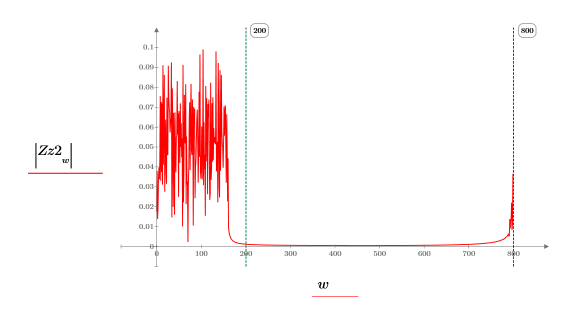
이 도표에는 변환 영역에서 신호를 생성하는 데 사용된 원래의 200개 점이 표시되어 있습니다. 스펙트럼의 위쪽 절반은 0이므로, 힐버트 변환기 필터가 올바르게 적용되었습니다.