예제: 스펙트럼 분석
coherence, cspectrum, pspectrum 및 snr 함수를 사용하여 신호 또는 신호 쌍에 대한 기여도, 상호 스펙트럼, 파워 스펙트럼 및 신호 대 잡음비를 계산합니다.
이 평균화 절차에 대해 설명은 Samuel Stearns와 Ruth David가 저술한 Signal Processing Algorithms(Prentice-Hall, Inc.)에 나와 있습니다.
파워 스펙트럼 - DFT 사용
소수의 데이터 점만 신호에 대응하는 값을 갖는 긴 시계열의 경우 노이즈나 0 값은 제외하고 신호의 주파수를 표시하는 파워 스펙트럼을 사용하는 것이 좋습니다.
1. 창함수 너비를 정의합니다.
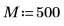
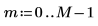
2. 신호가 0이 아닌 경우 사용 가능한 두 창함수 w1 및 w2를 정의합니다.
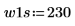 | 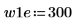 | 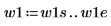 |
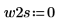 | 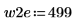 | 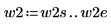 |
3. 창함수 너비를 사용 가능한 두 너비 중 하나로 설정합니다.
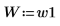
4. 신호 및 표본 주파수를 정의합니다.
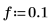
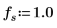
5. sin 함수를 사용하여 선택한 창 내부와 외부의 신호를 정의합니다.
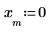
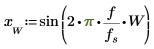
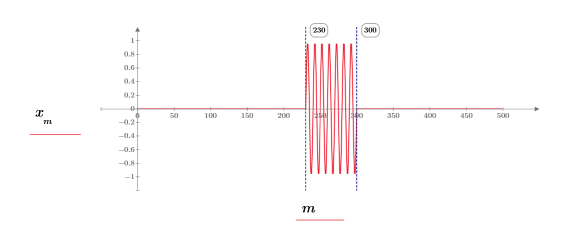
6. 신호를 도표화합니다.
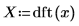
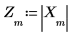
8. 결과 함수를 주파수 영역에서 도표화합니다.
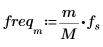
◦ 순수한 싸인파 신호의 경우 DFT 계수의 크기로 신호의 파워 스펙트럼을 양호하게 추정할 수 있습니다. 하지만 이 경우에는 신호의 DFT가 사각형 창의 변환(sinc 함수)과 컨볼루션된 구조적 신호의 주파수 컨텐트입니다.
◦ W= w2(단계 3) 설정은 창함수를 확장하여 싸인파가 230~300 사이에서 0~499 사이(계수 7.143x)에 존재하도록 만들어 두 피크의 크기를 35에서 250(계수 7.143x)으로 증가시킵니다.
◦ 피크가 발생하는 주파수는 그대로 유지됩니다.
파워 스펙트럼 - pspectrum 사용
pspectrum 함수는 원래 시계열을 중첩 세그먼트로 나눕니다. 이러한 세그먼트 각각은 DFT에 의해 변환되고 변환된 크기 계수는 평균화됩니다. 세그먼트의 길이가 신호에서 분석할 현상과 배율이 같은 경우 pspectrum 함수를 사용하여 원래 시계열에서 관심 부분의 크기를 보다 정확하게 추정할 수 있습니다.
일반적으로 신호의 길이는 적어도 n + 1이어야 합니다.
1. 신호의 길이, 중첩 비율 및 창 유형(테이퍼된 사각형)을 정의합니다.
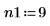 | 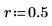 | 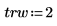 |
2. pspectrum 함수를 통해 중첩 비율 r을 사용하여 x를 n1개의 중첩하는 세그먼트로 분할하고 각 세그먼트에 테이퍼된 사각형 창함수를 적용하여 계산된 x의 파워 스펙트럼을 계산합니다.
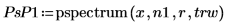
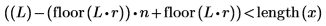
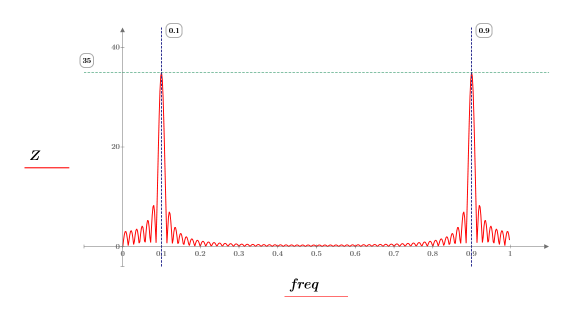
4. 정규화된 주파수 축으로 스펙트럼을 도표화합니다(1은 표본 주파수를 나타냄).
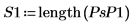
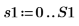
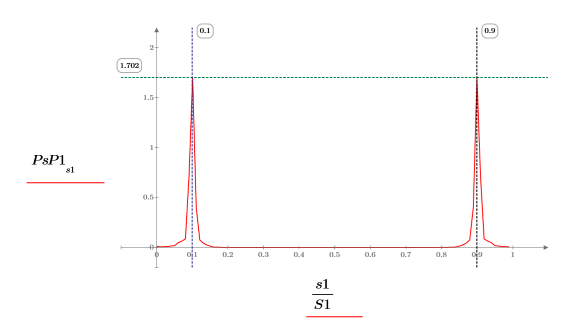
5. 스펙트럼의 평균 거듭곱을 계산합니다.
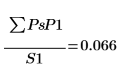
이것은 근사적으로 신호 x의 평균 제곱 값입니다.
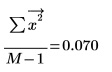
백색 노이즈의 pspectrum
백색 노이즈를 포함하는 신호의 파워 스펙트럼을 계산합니다. 상호 스펙트럼 계산에 두 번째 신호가 필요하므로 신호 두 개를 생성합니다. 해밍 창함수를 사용하여 데이터 블록에 테이퍼를 적용합니다.
1. 신호 너비를 정의합니다.
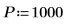
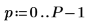
2. sin 및 rnd 함수를 사용하여 공통 주파수 fc의 두 신호를 정의합니다. rnd 함수는 0과 지정된 숫자 사이에서 균일하게 분포되는 난수의 벡터를 반환하므로 신호가 계속 다르게 유지됩니다.
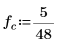
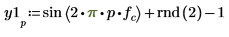
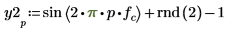
3. 두 신호의 처음 100개 표본을 도표화합니다.
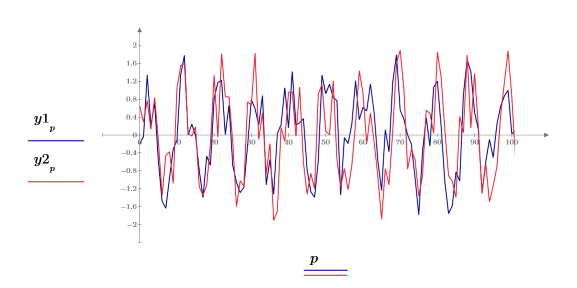
4. pspectrum 함수를 통해 중첩 비율 0.5를 사용하여 40개의 중첩하는 세그먼트로 분할하고 각 세그먼트에 해밍 창함수를 적용하여 y1의 파워 스펙트럼을 구합니다.
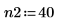 | 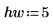 |
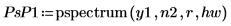 | |
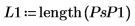 | 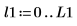 |
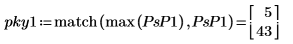
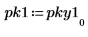
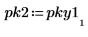
6. 스펙트럼을 데시벨 단위로 도표화합니다. 마커를 사용하여 공통 주파수와 최대 데시벨 값을 표시합니다.
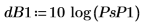
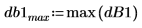
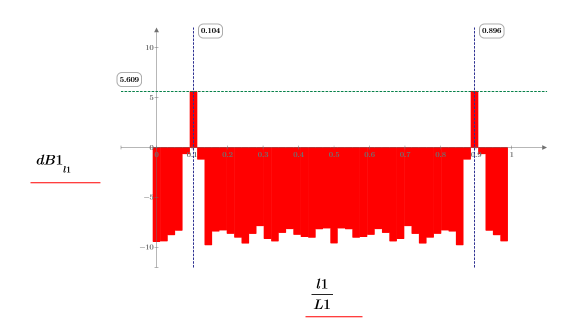
도표는 모든 신호 파워가 공통 주파수 fc 및 1-fc에서 발생한다는 것을 보여줍니다.
7. 노이즈 파워를 계산합니다.
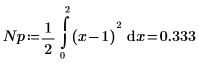
8. 노이즈 파워 게인을 dB 단위로 계산합니다.
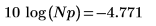
9. 위 두 주파수 표본을 스펙트럼 길이로 나누면 싸인 컴포넌트의 평균 전력인 0.5가 나와야 한다는 사실로부터 높이를 계산합니다.
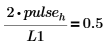 | 또는: | 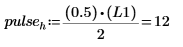 |
10. 이론적 높이와 실제 높이를 데시벨 단위로 비교합니다.
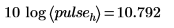
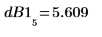
cspectrum 함수
일반적으로 두 신호의 유사도를 감지하는 데 상호 스펙트럼이 사용됩니다. 예를 들어, 알려진 음성 파형(예: 모음 'a')과 알려지지 않은 음성 파형(예: 단어 'apple')을 비교하여 알려지지 않은 파형에 알려진 파형이 존재하는지 확인할 수 있습니다. 시계열의 파워 스펙트럼이 해당 자기상관과 유사한 것처럼 두 시계열의 상호 스펙트럼은 해당 상호상관과 유사합니다. 정적인 임의 시퀀스의 경우 스펙트럼 함수는 상관성 함수와 동일한 값을 구합니다.
1. 중첩 비율 0.5로 40개의 중첩하는 세그먼트를 사용하고 각 세그먼트에 테이퍼된 사각형 창함수를 적용하여 신호 y1 및 y2에 cspectrum 함수를 적용합니다.
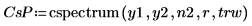
2. 스펙트럼을 데시벨 단위로 도표화합니다.
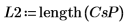 | 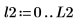 |
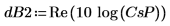 | |
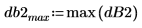 |
3. 상호 스펙트럼을 도표화합니다. 이 상호 스펙트럼은 복소수이므로 크기에 log 함수를 적용해야 한다는 것을 잊지 마십시오.
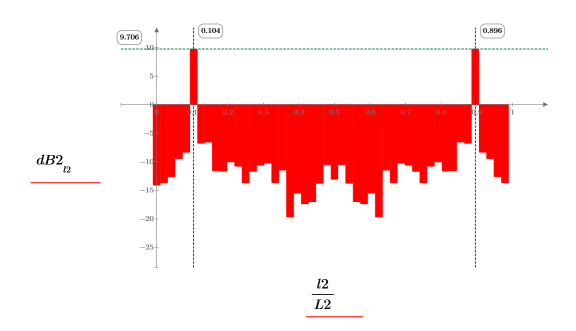
y1 및 y2의 상호 스펙트럼은 공통 주파수 fc 및 1- fc에서 피크를 보여줍니다.
coherence 및 snr 함수
coherence 함수는 한 신호에 대한 다른 신호의 선형 종속성을 측정하고, 두 신호의 상호 스펙트럼 제곱 크기를 두 파워 스펙트럼으로 나눈 것과 동일하며, 값 범위는 0부터 1 사이입니다. coherence 함수의 값 1은 해당 주파수 구간에서 두 신호 모두 노이즈가 없는 강력한 컴포넌트가 있다는 것을 나타내고, 값 0은 해당 주파수 구간에 대부분 노이즈가 있다는 것을 나타냅니다.
신호 대 잡음비 snr 함수는 coherence 함수를 1에서 coherence 함수를 뺀 값으로 나눈 것과 같으며, 신호의 강도와 센서 또는 배경 노이즈의 강도 간 비율에 비례하는 모든 컴포넌트 대역에서 두 신호가 강한 컴포넌트를 갖는 위치에서 최대값을 갖습니다.
1. 중첩 비율 0.5로 40개의 중첩하는 세그먼트를 사용하고 각 세그먼트에 해밍 창함수를 적용하여 신호 y1 및 y2에 coherence 함수를 적용합니다.
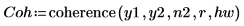 | |
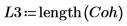 | 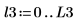 |
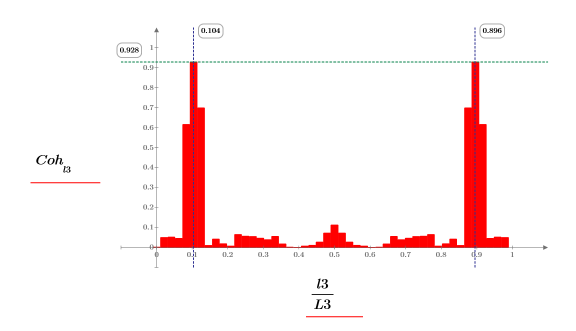
2. coherence 함수를 도표화합니다. 마커를 사용하여 공통 주파수와 최대값을 표시합니다.
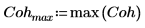
3. 중첩 비율 0.5로 40개의 중첩하는 세그먼트를 사용하고 각 세그먼트에 해밍 창함수를 적용하여 신호 y1 및 y2에 snr 함수를 적용합니다.
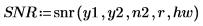 | |
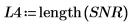 | 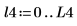 |
4. 신호 대 잡음비 함수를 도표화합니다. 마커를 사용하여 공통 주파수와 최대값을 표시합니다.
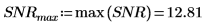
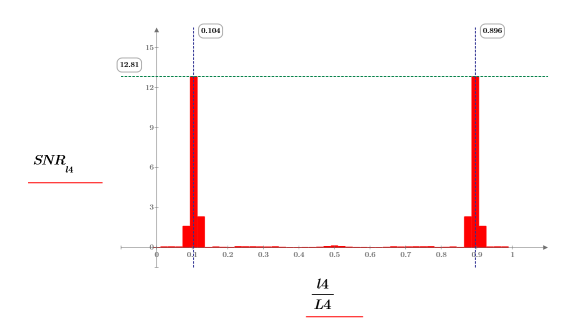
coherence 및 snr 함수 모두 두 신호의 단일 주파수 컴포넌트에서 최대값을 가지며 양 옆의 작은 막대로 표시되는 추가적인 노이즈를 포함합니다.