예제: 제약 조건이 있는 풀이 구간

풀이 구간 > 예제: 제약 조건이 있는 풀이 구간

예제: 제약 조건이 있는 풀이 구간

방정식 시스템 풀이에서 제약 조건이 있는 풀이 구간을 사용합니다.

원이 선과 교차하는 상황을 생각해 봅니다. 제약이 없어서 여러 개의 해가 존재하면 추측값을 통해 구할 해를 결정합니다.

1. 풀이 구간을 삽입하고, 추측값과 제약 조건을 정의한 다음 find 풀이 시스템 함수를 사용하여 선과 원 간의 교차점을 구합니다.

2. 원, 선 및 교차점을 도표화합니다.

<region id="ID0E6ECKB" height="465.532348506672" width="576.200000014902" actualWidth="576.200000014902" actualHeight="465.532348506672" top="864.00000000000011" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="57">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="58">
          <traceStyle color="#FF800080" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="59">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="60">
          <traceStyle color="#FFFF0000" symbol="filledRectangle" line-weight="2" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.600000014902" height="407.932348506672" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-4" end="4">
          <axisLine position="origin" positionticmark="3" legendWidth="231.73" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">ξ</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">xval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="61">
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3" end="6">
          <axisLine position="origin" positionticmark="4" legendWidth="117.872666636904" />
          <axisGrid>
            <gridFrequency>10</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <minus />
                    <real>6</real>
                    <apply>
                      <pow />
                      <id xml:space="preserve">x</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <neg />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <minus />
                      <real>6</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve">x</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <minus />
                  <real>2</real>
                  <id xml:space="preserve">ξ</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">yval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="62">
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

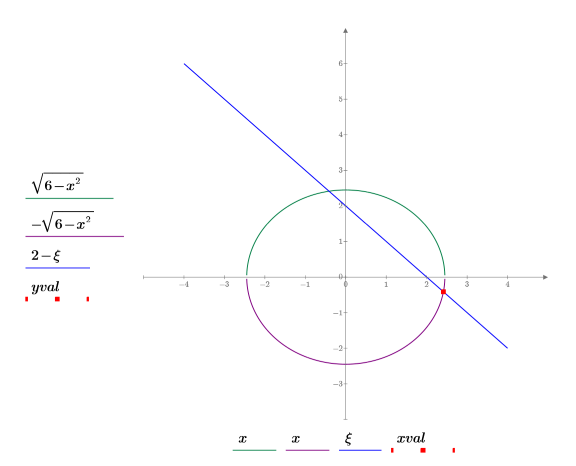
도표를 통해 이 해가 두 교차점 중 하나에 해당하며 풀이 시스템은 추측값에 가장 가까운 점을 선택한다는 것을 알 수 있습니다.

3. 추측값을 변경하고 해를 다시 계산합니다.

4. 원, 선 및 교차점을 도표화합니다.

<region id="ID0EDICKB" height="478.932348506672" width="575.200000014902" actualWidth="575.200000014902" actualHeight="478.932348506672" top="1766.4000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="70">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="71">
          <traceStyle color="#FF800080" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="72">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="73">
          <traceStyle color="#FFFF0000" symbol="point" line-weight="2" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="417.600000014902" height="421.332348506672" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-4" end="4">
          <axisLine position="origin" positionticmark="3" legendWidth="231.73" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">ξ</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">xval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="74">
              <real xmlns="http://schemas.mathsoft.com/math50">-3.0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3" end="6">
          <axisLine position="origin" positionticmark="4" legendWidth="117.872666636904" />
          <axisGrid>
            <gridFrequency>10</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <minus />
                    <real>6</real>
                    <apply>
                      <pow />
                      <id xml:space="preserve">x</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <neg />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <minus />
                      <real>6</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve">x</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <minus />
                  <real>2</real>
                  <id xml:space="preserve">ξ</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">yval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="75">
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </startValue>
            <secondTickValue resultRef="76">
              <real xmlns="http://schemas.mathsoft.com/math50">-2</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

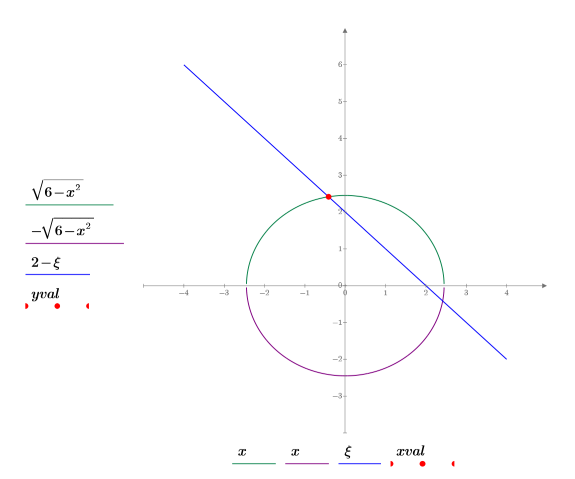
도표를 통해 이 해가 두 번째 교차점에 해당하며 풀이 시스템은 새 추측값에 가장 가까운 점을 선택한다는 것을 알 수 있습니다.

5. x > a 형태의 제약 조건을 추가합니다. 여기서 a는 상수입니다. 이제 선 왼쪽에 있는 영역이 고려 대상에서 제외됩니다.

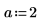
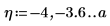
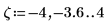
6. 원, 선 및 교차점을 도표화합니다. 세로 마커를 사용하여 선 a를 표시합니다.

<region id="ID0E3MCKB" height="478.932348506672" width="575.200000014902" actualWidth="575.200000014902" actualHeight="478.932348506672" top="2956.8000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="88">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="89">
          <traceStyle color="#FF800080" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="90">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="91">
          <traceStyle color="#FFFF0000" symbol="point" line-weight="2" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="417.600000014902" height="421.332348506672" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-4" end="4">
          <axisLine position="origin" positionticmark="3" legendWidth="231.73" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="92" display="true" color="#FFCB4C23" line-style="Dash" value="2">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">ξ</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">xval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="93">
              <real xmlns="http://schemas.mathsoft.com/math50">-3.0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3" end="6">
          <axisLine position="origin" positionticmark="4" legendWidth="117.872666636904" />
          <axisGrid>
            <gridFrequency>10</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <minus />
                    <real>6</real>
                    <apply>
                      <pow />
                      <id xml:space="preserve">x</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <neg />
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <minus />
                      <real>6</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve">x</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <minus />
                  <real>2</real>
                  <id xml:space="preserve">ξ</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">yval</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="94">
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </startValue>
            <secondTickValue resultRef="95">
              <real xmlns="http://schemas.mathsoft.com/math50">-2</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

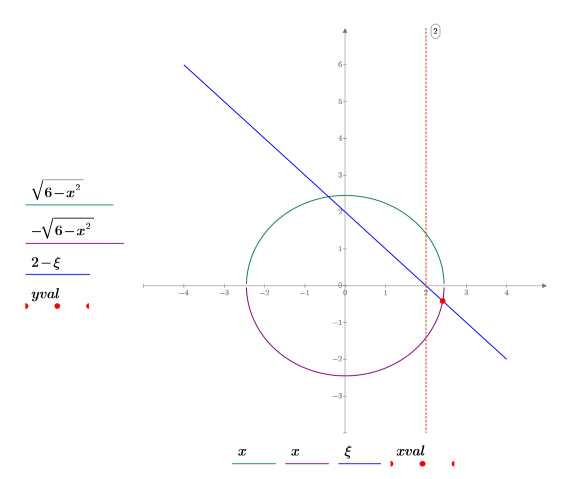
도표를 통해 이 해가 첫 번째 교차점(유일한 해)에 해당한다는 것을 알 수 있습니다. 이것은 풀이 시스템이 새 제약 조건을 충족해야 하기 때문입니다.