예제: 신호 창함수
다음 함수를 사용하여 신호 창 동작을 수행합니다.
이상적/절단 저역 통과 임펄스 반응
1. 정규화된 차단 주파수 0.15를 사용하여 이상적 저역 통과 필터의 임펄스 반응 h를 정의합니다.
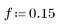
2. 임펄스 반응을 정의합니다.
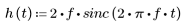
실현 가능한 유한 길이 필터는 유한 임펄스 반응을 가져야 하므로 이상적 응답을 관리 가능한 몇 개의 항으로 잘라야 합니다.
3. 주파수 응답에 창함수를 적용하지 않은 직접 자르기의 효과를 확인하기 위해서 이상적 응답의 중앙 N 항으로 구성되어 단순한 이동으로 필터 효과를 내는 길이 N 필터를 정의합니다.
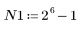
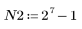
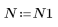
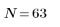
연습으로 N을 N2로 설정한 다음, 이후의 예제에서 항 수를 늘려 효과를 관찰합니다.
4. 항 범위 전체에 임펄스 반응 함수를 적용하고 결과 함수를 도표화합니다.
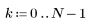
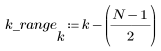
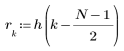
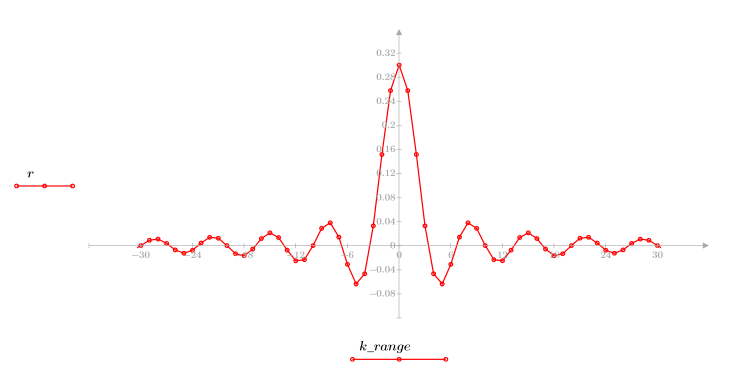
5. gain 함수를 사용하여 이 잘려진 신호의 주파수 응답을 계산합니다. 먼저 주파수 범위(표본 주파수의 배수)를 정의합니다.
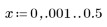
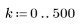
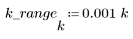
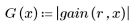
6. gain 함수의 이산 크기를 새 배열로 수집합니다.
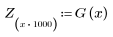
7. G의 최대 크기와 해당하는 주파수를 찾습니다.
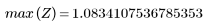
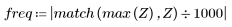
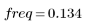
항 수가 N1=63일 때 gain의 최대값 1.083은 주파수 freq=0.134일 때 발생합니다.
항 수가 N2=127일 때 gain의 최대값 1.092는 주파수 freq=0.142일 때 발생하여 대역 경계 가까이로 이동합니다.
주파수 freq=0.2에서 gain은 거의 0으로 줄어듭니다. 다음 각 예제에서 이 주파수 주위의 gain을 비교합니다.
8. 정의된 범위에 대해 gain 함수를 도표화하여 크기가 최대값이 되는 주파수를 표시합니다.
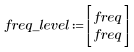
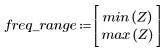
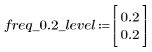
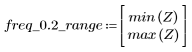
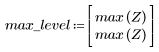
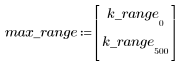
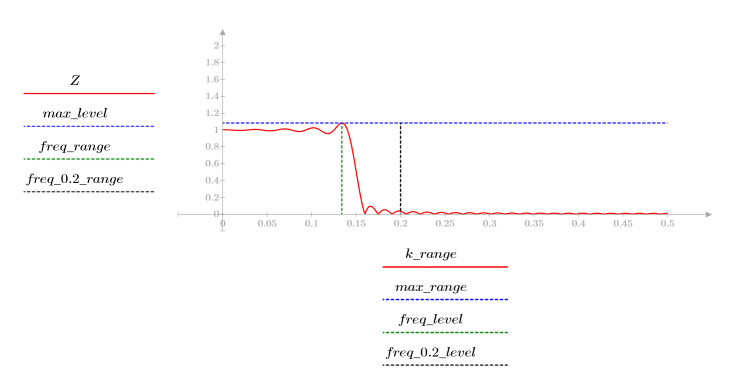
통과 대역 경계에서 발생하는 오버슈트는 깁스 현상이라고 알려져 있습니다. 필터 차수 N을 N1=63부터 N2=127까지 증가시키면 오버슈트가 대역 경계에 더 가까워지지만 진폭이 줄어들지는 않습니다.
필터 차수 N 값이 증가하면 1부터 0까지의 변환이 더 가파르게 됩니다.
더 바람직한 주파수 응답을 생성하는 방법 한 가지는 이상적 임펄스 반응에 창함수를 적용하여 필터 임펄스 응답의 경계에서 더 부드럽게 0으로 변환되게 만드는 것입니다. 창함수는 응답 벡터 r과 항 대 항으로 곱해집니다.
삼각형 창함수
triangular 함수는 너비 N인 삼각형 또는 버틀렛 창함수를 구합니다.
결과 벡터의 j번째 요소는 다음을 통해 구합니다.
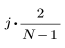
다음 조건인 경우
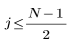
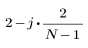
다음 조건인 경우
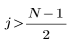
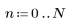
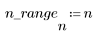
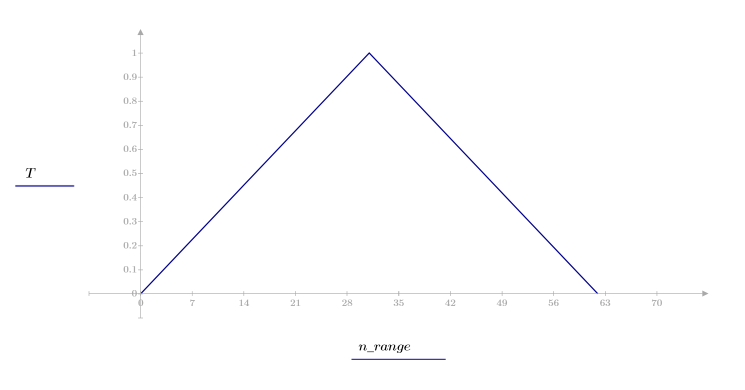
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
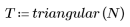
2. 창을 씌운 충격 반응을 계산합니다.
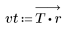
3. gain 함수를 사용하여 계수 vt, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
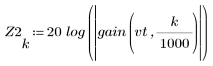
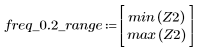
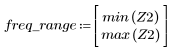
해닝 창함수
hanning 함수는 너비 N인 해닝 창함수를 구합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
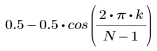
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
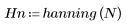
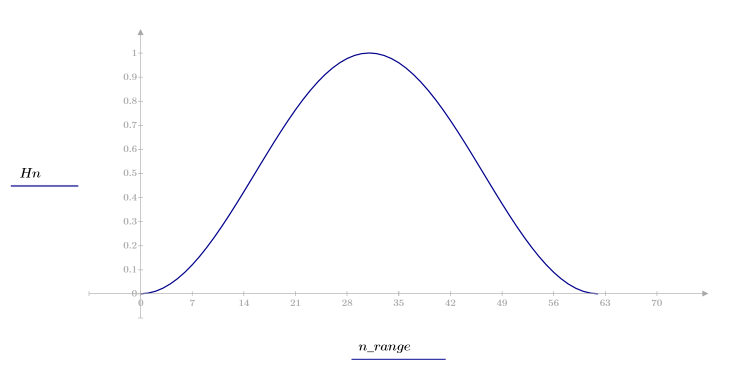
2. 창을 씌운 충격 반응을 계산합니다.
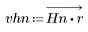
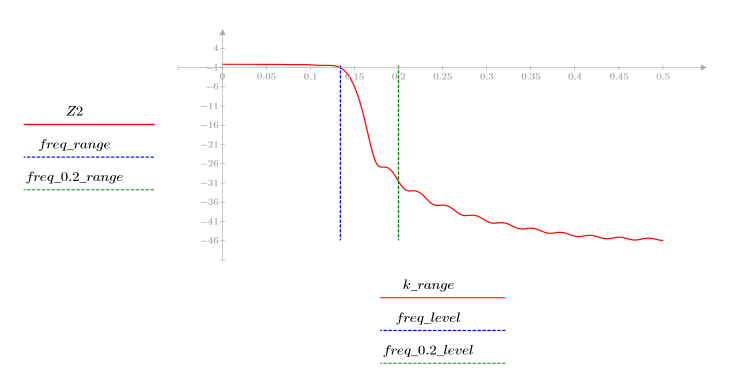
3. gain 함수를 사용하여 계수 vhn, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
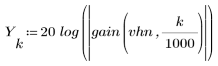
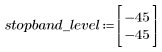
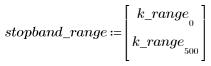
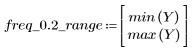
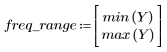
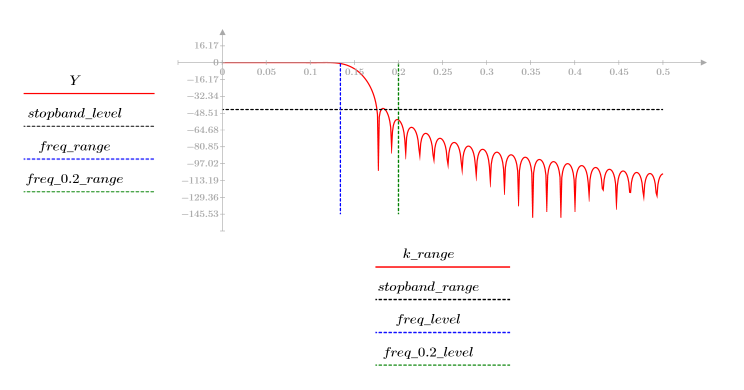
정지 대역(stopband) 맥동이 약 -45dB입니다.
해밍 창함수
hamming 함수는 너비 N인 해밍 창함수를 구합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
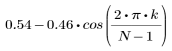
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
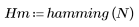
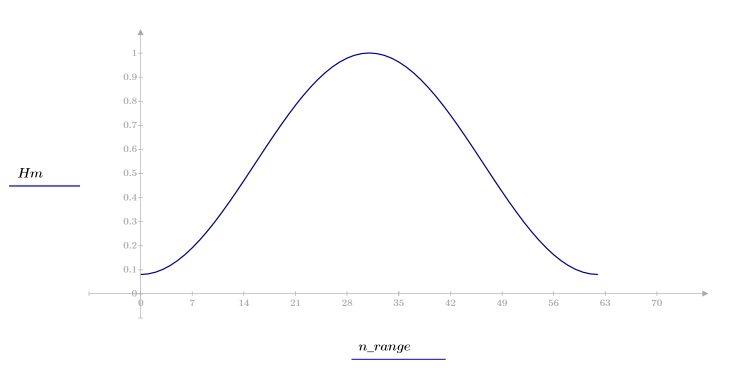
2. 창을 씌운 충격 반응을 계산합니다.
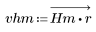
3. gain 함수를 사용하여 계수 vhm, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
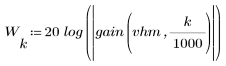
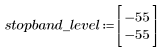
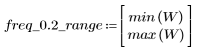
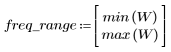
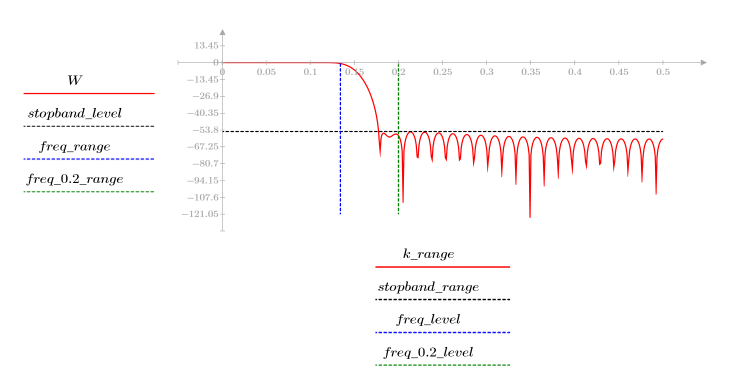
정지 대역 맥동이 약 -55dB입니다.
블랙맨 창함수
blackman 함수는 너비 N인 블랙맨 창함수를 구합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
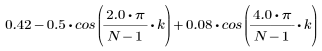
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
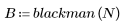
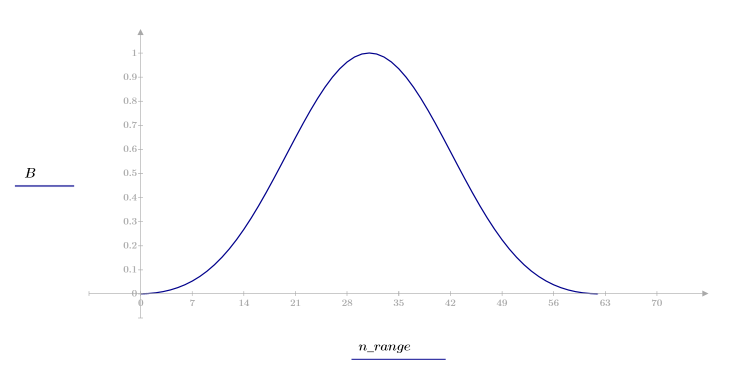
2. 창을 씌운 충격 반응을 계산합니다.
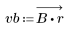
3. gain 함수를 사용하여 계수 vb, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
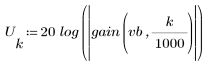
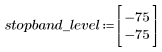
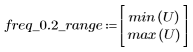
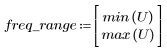
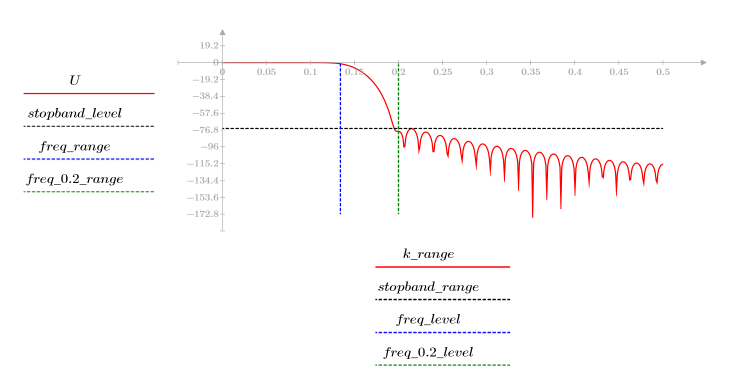
정지 대역 맥동이 약 -75dB입니다.
너틀 창함수
nuttall 함수는 너비 N인 너틀 창함수를 구합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
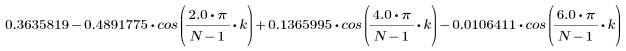
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
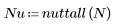
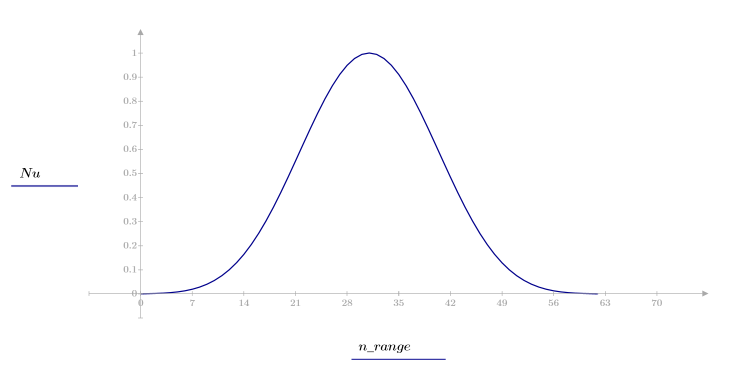
2. 창을 씌운 충격 반응을 계산합니다.
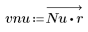
3. gain 함수를 사용하여 계수 vnu, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
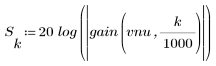
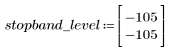
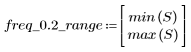
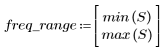
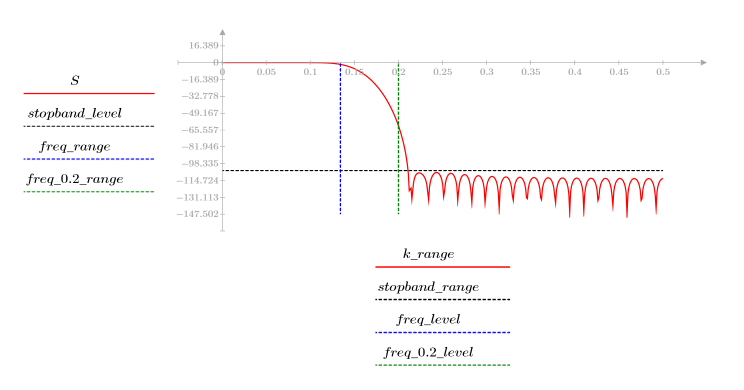
정지 대역 맥동이 약 -105dB입니다.
테이퍼된 사각형 창함수
taprect 함수는 너비 N인 테이퍼된 사각형 창함수를 구합니다.
이 창함수는 높이 1인 중간 부분에서 수평이고 코사인 곡선에서 형성된 테이퍼된 끝을 가집니다. 오른쪽 및 왼쪽에서는 다음 값을 사용합니다.
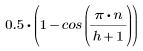
여기서
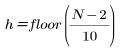
n이 0부터 h까지 변합니다.
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
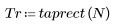
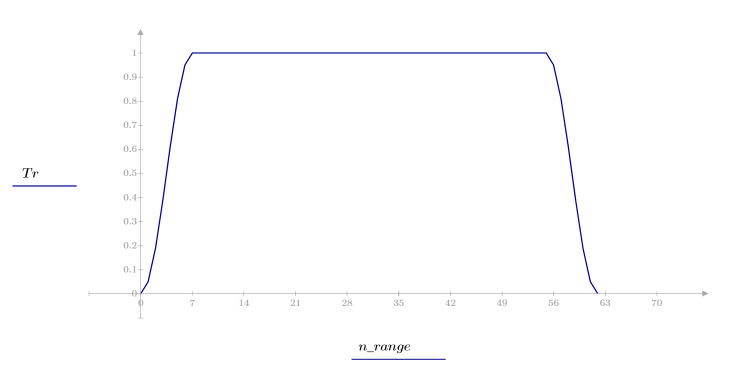
2. 창을 씌운 충격 반응을 계산합니다.
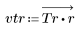
3. gain 함수를 사용하여 계수 vtr, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
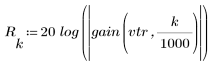
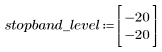
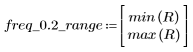
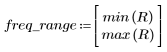
가우시안 창함수
gaussian 함수는 너비 N과 매개변수 a인 가우시안 창함수를 구합니다. 숫자 a는 가우시안 분산의 역에 비례하는 실수이며 2 < a < 20을 충족해야 합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
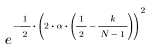
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
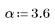
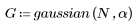
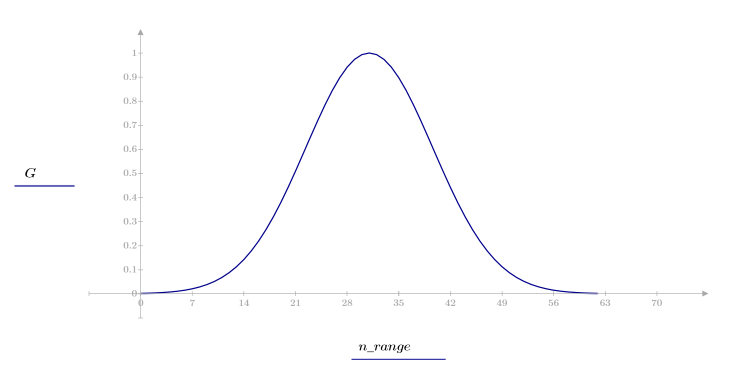
2. 창을 씌운 충격 반응을 계산합니다.
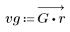
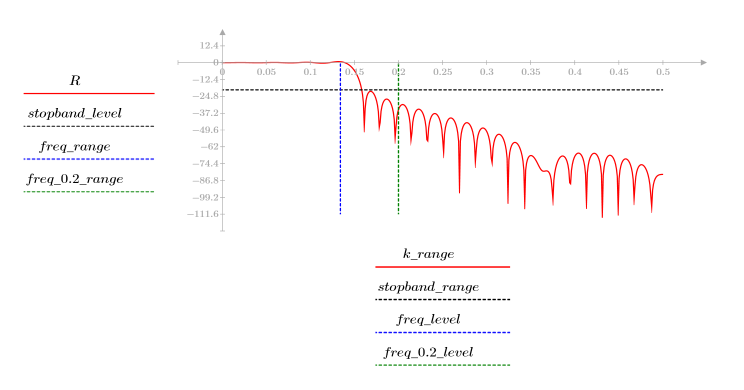
3. gain 함수를 사용하여 계수 vg, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
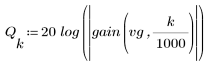
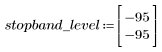
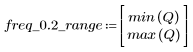
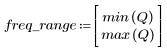
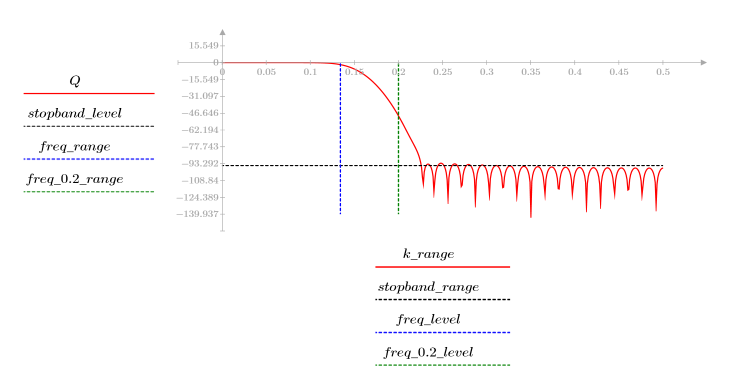
정지 대역 맥동이 약 -95dB입니다.
카이저 창함수
kaiser 함수는 너비 N과 매개변수 b인 카이저 창함수를 구합니다. 매개변수 b는 2≤b≤20을 충족해야 합니다.
결과 벡터의 k번째 요소는 다음을 통해 구합니다.
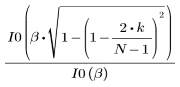
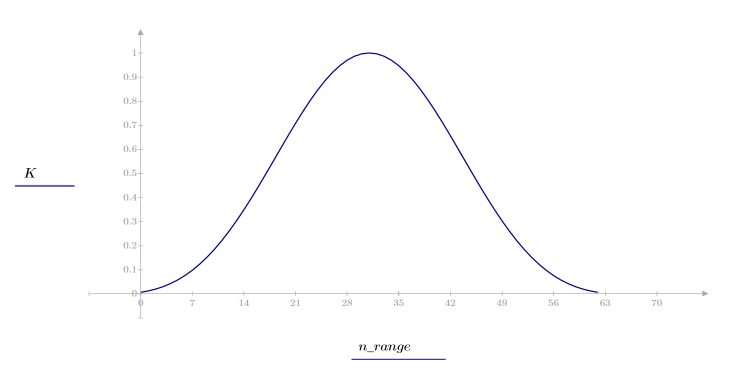
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
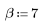
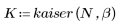
2. 창을 씌운 충격 반응을 계산합니다.
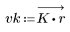
3. gain 함수를 사용하여 계수 vk, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
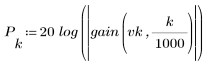
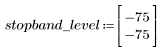
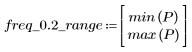
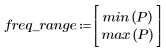
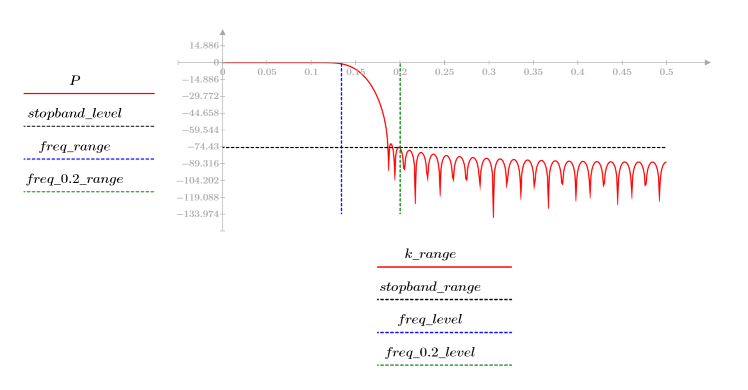
정지 대역 맥동이 약 -75dB입니다.
체비셰프 창함수
cheby 함수는 너비 N과 매개변수 b인 체비셰프 또는 ER(Equi-Ripple) 창함수를 구합니다. 매개변수 b는 사이드로브 맥동을 dB 단위로 지정하며 1 < b를 충족해야 합니다. 대개 b는 50보다 큽니다. 이 창함수의 길이는 홀수여야 합니다. 체비셰프 창함수는 단위 원 주위의 점에서 계산된 체비셰프 다항식의 역 이산 푸리에 변환을 구해 계산합니다. 이 창함수에 대한 자세한 내용은 Programs for Digital Signal Processing(IEEE Press)을 참조하십시오.
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
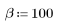
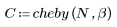
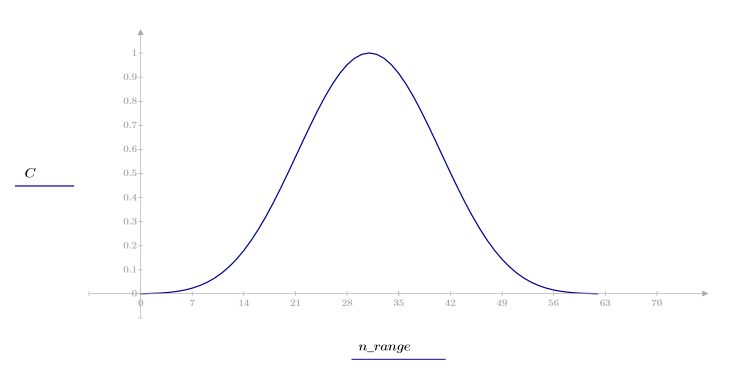
2. 창을 씌운 충격 반응을 계산합니다.
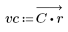
3. gain 함수를 사용하여 계수 vc, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
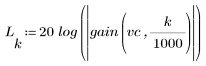
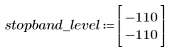
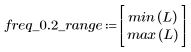
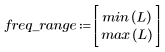
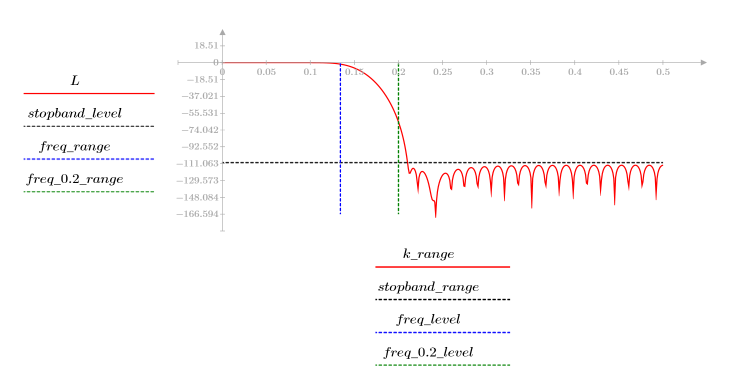
정지 대역 맥동이 약 -110dB입니다.
코사인 테이퍼 창함수
costaper 함수는 코사인 곡선을 따르는 테이퍼된 꼬리를 포함한 사각형 창함수를 반환한다는 점에서 taprect 함수와 유사합니다. 하지만 매개변수를 사용하여 코사인 곡선으로 생성되는 창함수 부분의 백분율을 지정할 수 있다는 점이 다릅니다. 이 매개변수는 0에서 1 사이여야 합니다. 값이 0이면 사각형 창함수가 반환되고 값이 1이면 상승 코사인 곡선이 반환됩니다.
창함수의 테이퍼된 부분에서 k번째 요소의 값은 다음과 같이 주어집니다.
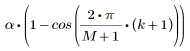
여기서 M은 꼬리 중 하나에 속하는 창함수 요소의 수이며 a-N으로 주어집니다.
1. 함수를 적용하여 차수 N을 필터링하고 결과 벡터를 도표화합니다.
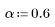
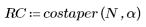
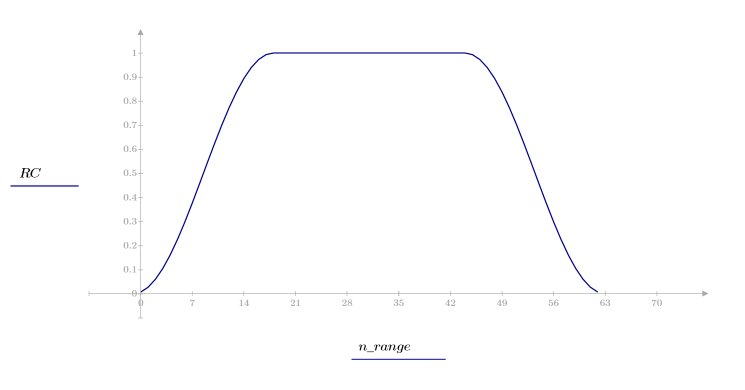
2. 창을 씌운 충격 반응을 계산합니다.
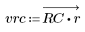
3. gain 함수를 사용하여 계수 vrc, 주파수 k/1000에서 이 필터의 dB 단위 게인을 계산하고 도표화합니다.
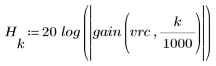
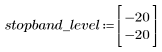
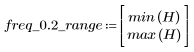
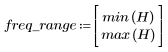
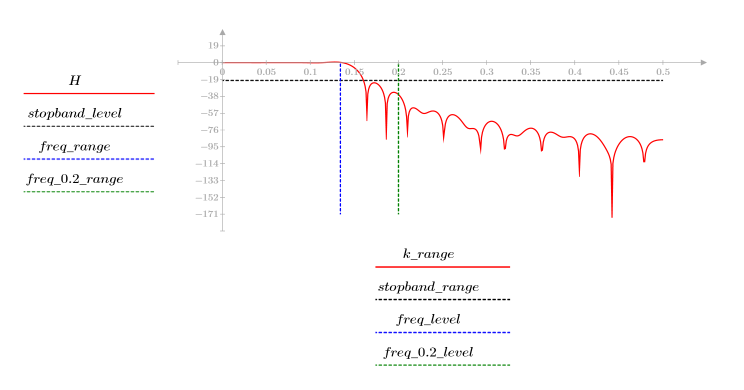
정지 대역 맥동이 약 -20dB입니다.
참조
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications, Prentice-Hall(1987년)
• Lawrence R. Rabiner 및 Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, Inc.(1975년)
• T. W. Parks 및 C. S. Burrus, Digital Filter Design, Wiley-Interscience(1987년)