예제: 주입된 반복법 및 계차 방정식

벡터, 행렬 및 표 > 배열 작업 > 예제: 주입된 반복법 및 계차 방정식

주입된 반복법을 사용하여 해를 추정합니다.

제곱근

바빌로니아 방법(Babylonian method)을 사용하여 값의 제곱근 근사해를 구합니다.

1. 양의 실수 X와 해당 제곱근의 추측값을 정의합니다.

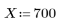
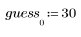
첫째 추측값은 벡터의 첫째 요소로 정의됩니다.

2. N을 반복 횟수로 정의합니다.

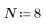
3. 제곱근의 추정치를 새로 계산합니다.

<region id="ID0EW4VGB" top="336" left="48" width="168.866666666667" height="52.473" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id label="None">guess</id>
        <apply>
          <plus />
          <id label="None">i</id>
          <real>1</real>
        </apply>
      </apply>
      <apply>
        <mult />
        <parens>
          <apply>
            <plus />
            <apply>
              <indexer />
              <id>guess</id>
              <id>i</id>
            </apply>
            <apply>
              <div />
              <id>X</id>
              <apply>
                <indexer />
                <id>guess</id>
                <id>i</id>
              </apply>
            </apply>
          </apply>
        </parens>
        <apply>
          <div />
          <real>1</real>
          <real>2</real>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" />
    </resultFormat>
  </math>
</region>

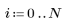
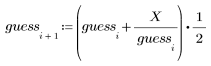
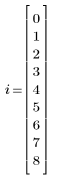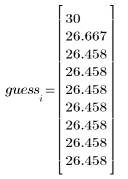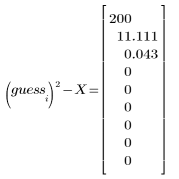기본 제공 제곱근 함수의 결과는 다음과 같습니다.

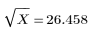
4. 추정치의 벡터를 도표화합니다.

<region id="ID0ERCWGB" top="888" left="0" width="622" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FF00008B" symbol="rhombus" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="bottom" positionticmark="-1" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">i_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">guess</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

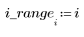
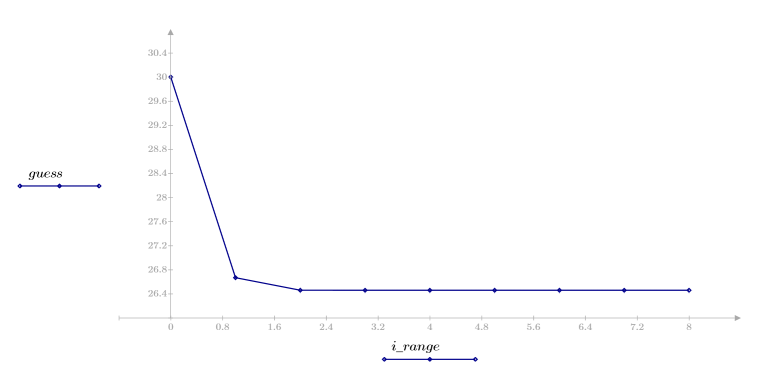
여기서는 수렴이 매우 빨리 일어납니다. 다른 상황에서는 문제의 요구 사항에 맞게 반복 횟수 N을 적절히 늘릴 수 있습니다.

계차 방정식 시스템

변수가 4개인 감염 모델을 살펴봅니다.

• inf - 감염자 수

• sus - 의심 환자 수

• dec - 사망자 수

• rec - 회복된 환자 수

1. 동시 반복을 위한 기초값을 정의합니다.

2. 계차 방정식 시스템을 정의합니다.

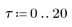
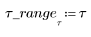
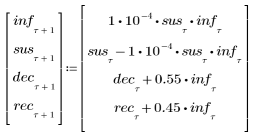
3. 감염 모델의 전개 상황을 살펴보려는 기간을 대상으로 변수 4개를 도표화합니다.

<region id="ID0EQNWGB" top="1920" left="0" width="668" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="DashDotDot">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FFFFA500" symbol="none" line-weight="1" line-style="DashDot">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">τ_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">inf</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">sus</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">dec</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">rec</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

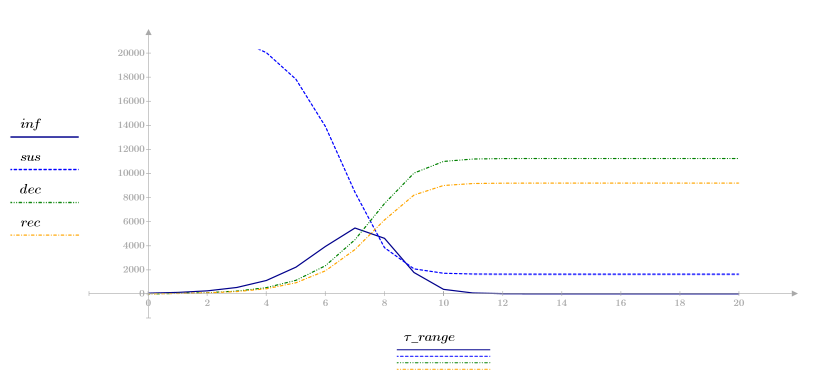
행렬 계차 방정식

이전 상태에 상태 변환 행렬을 곱해 현재 상태를 구하는 벡터 시계열 형식의 마르코프 과정(Markov process)을 살펴봅니다.

1. 초기 벡터 상태와 상태 변환 행렬 A를 정의합니다.

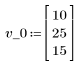
2. 반복 과정을 정의합니다.

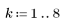
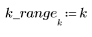
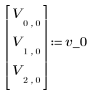
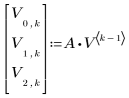
3. 벡터의 최종 상태를 계산합니다.

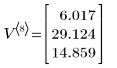
행렬 V에는 과정의 내역이 포함됩니다.