예제: 잉여 분석
데이터 집합의 잉여값을 계산하여 해당 집합이 선형으로 분포해 있는지 확인합니다. 예측을 위해 회귀 모델을 사용하기 전에 선형 모델을 가정할 만한 조건이 충족되었는지 확인합니다.
• 오차 사이에 상관 관계가 없어야 합니다.
• X에 포함된 임의의 값에 대해 오차가 0과 불변 분산의 평균으로 정규 분포해 있어야 합니다.
표준화된 잉여
잉여의 상대적 규모를 해석하기 위해 이를 표준화할 수 있습니다. 그러려면 잉여값을 오차 표준 편차에 대한 추정치로 나눠야 합니다.
1. 다음과 같은 데이터 집합을 정의합니다.
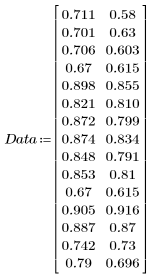
2. 데이터 집합을 도표화합니다.
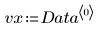
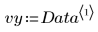
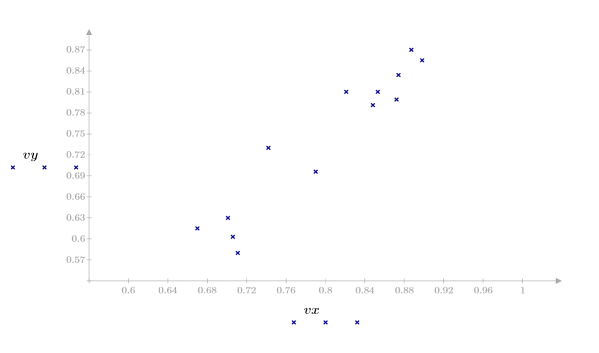
도표를 보면 데이터가 선형으로 분포해 있는 것으로 판단할 수 있습니다. 이는 상관 계수가 1에 가깝다는 사실로도 확인할 수 있습니다.
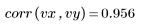
3. 최적합 선을 정의합니다.
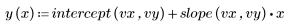
4. 측정한 값에서 적합 값을 뺍니다.
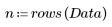
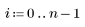
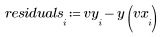
5. 잉여값을 추정치의 표준 오차로 나눕니다.
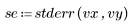
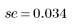
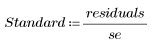
스튜던트화된 잉여
스튜던트화된 잉여값, 즉 표준화하여 조정을 거친 잉여값은 표준 오차에 대해 흔히 사용되는 또 다른 추정치입니다. 이 추정에서는 x의 각 값과 x의 평균 사이의 간격을 조정합니다.
1. 값과 평균 사이의 간격을 구합니다.
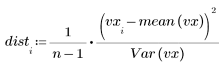
2. 각 잉여값에 사용되는 표준 편차를 정의합니다.

3. 스튜던트화된 잉여값을 정의합니다.
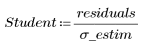
스튜던트화된 잉여값은 오차 분산에서 발견되는 각 점 사이의 차이를 설명하므로 표준화된 잉여값보다 더 정확합니다. 그러나 대개의 경우 표준화하여 구한 잉여값과 스튜던트화하여 구한 잉여값 자체는 서로 크게 다르지 않습니다.
 |  |
4. polyfitstat를 호출합니다. 스튜던트화된 잉여값을 포함하는 관측 진단값의 부분 행렬을 표시합니다.
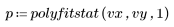
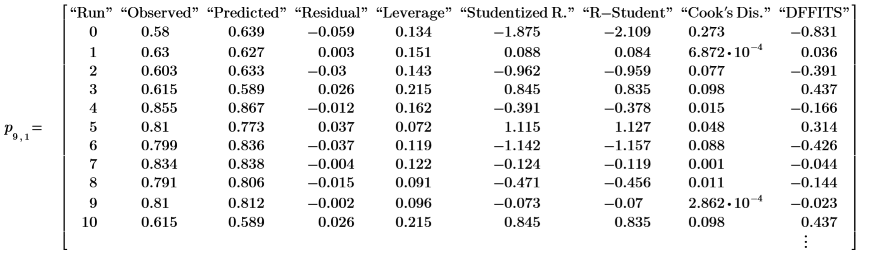
선형성 확인
Data 집합이 선형으로 관계를 맺고 있는지 확인합니다. 곡선형 관계가 있는 무작위 표본을 사용하여 가정에 반하는 예를 만듭니다. 데이터가 선형으로 관련되어 있고 오차가 정규 분포해 있으면 산점도에서 뚜렷한 패턴이 나타나지 않습니다. 가설로 세운 오차 평균인 0을 중심으로 하여 점이 무작위로 산개합니다.
1. x 값과 예측된 y 값을 기준으로 잉여값을 도표화합니다.
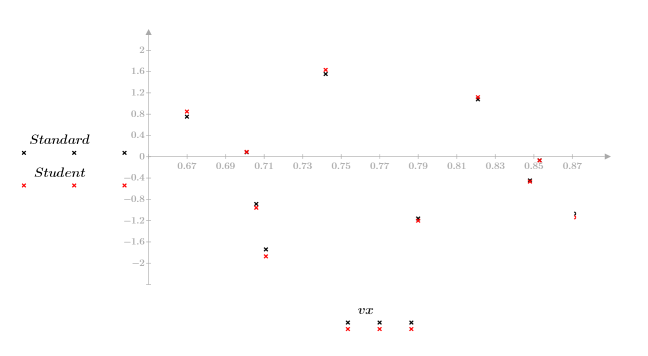
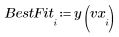
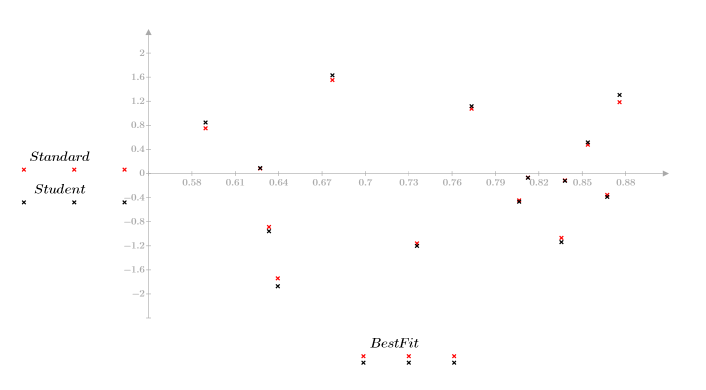
잉여값의 패턴이 뚜렷하지 않는다는 것은 데이터가 선형으로 관계를 맺고 있음을 의미합니다.
2. 이번에는 2차 관계가 있는 점의 무작위 표본을 생성합니다.
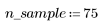
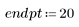
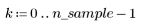
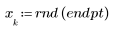
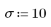
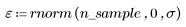
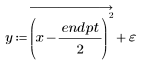
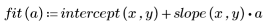
3. 잉여값의 상대 강도를 도표화합니다.
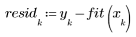
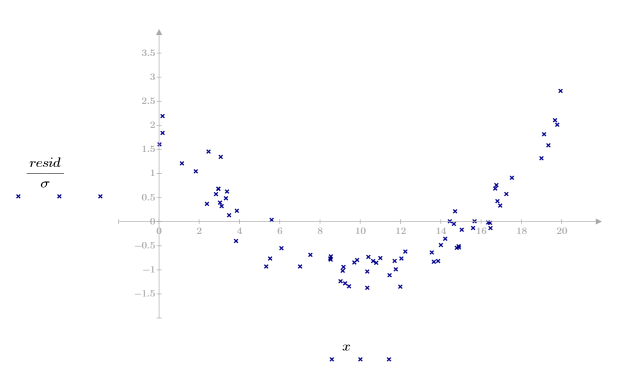
데이터의 2차 패턴이 잉여값의 산점도에 반영되어 나타납니다. 이 데이터는 선형으로 관련되어 있지 않습니다.
불변 오차 분산 확인
Data 집합에서 오차 분산의 어떠한 패턴도 확인되지 않았습니다. 데이터가 선형으로 표시되지만 오차 분산이 정규 분포해 있지 않도록 하여 가정에 반하는 예를 만듭니다. 잉여값의 산점도에는 왼쪽에서 오른쪽으로 더 퍼지거나 더 모여드는 패턴이 나타납니다.
1. 왼쪽에서 오른쪽으로 점점 더 퍼지며 산개하는 점의 무작위 표본을 생성합니다.
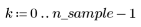
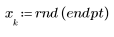
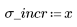
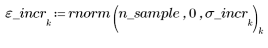
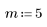
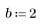
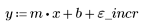
2. 최적합 선을 구합니다. 무작위 데이터 집합과 적합식을 도표화합니다.
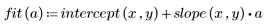
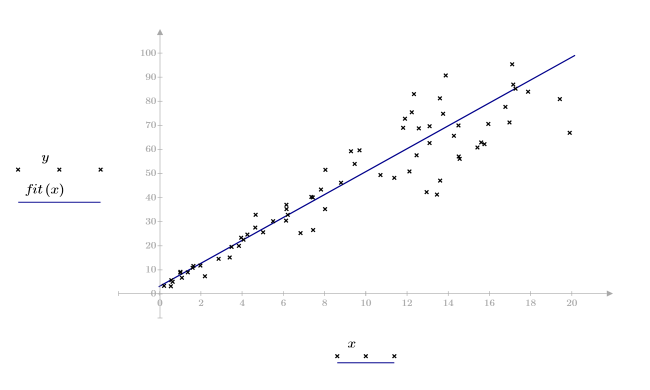
상관 계수가 1에 가깝습니다. 이는 데이터가 선형으로 관련되어 있음을 의미합니다.
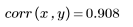
3. 잉여값의 상대 강도를 도표화합니다.
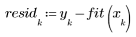
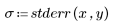
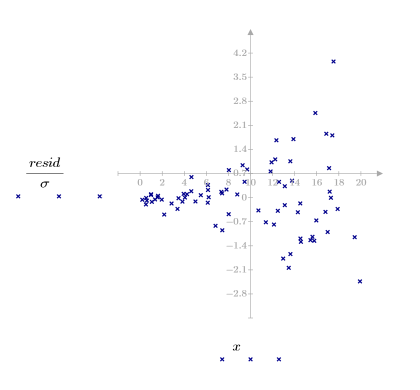
여기서는 잉여값의 산점도가 무작위로 분포해 있지 않은 것으로 해석할 수 있습니다. 잉여 도표의 점들이 왼쪽에서 오른쪽으로 갈수록 점점 더 퍼지며 산개하고 있기 때문입니다.
오차 상관 관계 확인
더빈-왓슨(Durbin-Watson) 통계값을 사용하여 선형 회귀 모델의 인접한 오차 항들이 상관 관계를 맺고 있는지 확인할 수 있습니다.
Data 집합에 대한 더빈-왓슨 통계값을 구합니다.
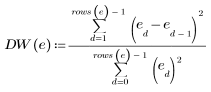
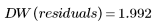
더빈-왓슨 통계값의 범위는 0에서 4까지입니다. 인접한 항 사이에 상관 관계가 없으면 더빈-왓슨 값이 2에 가깝게 나타납니다. 더빈-왓슨 값이 2보다 작으면 양의 인접 상관 관계가 있다는 의미이고, 이 값이 2보다 크면 음의 상관 관계가 있다는 의미입니다.
더빈-왓슨 통계값은 최소자승 B-스플라인을 구하는 데 사용됩니다. 그러나 차수가 높은 상관 관계, 즉 인접하지 않은 상관 관계는 더빈-왓슨 통계값으로 찾아낼 수 없습니다. 인접한 오차 사이에 상관 관계가 없는 경우에는 일반적으로 이러한 유형의 상관 관계도 발생하지 않습니다.
더빈-왓슨 통계값은 polyfitstat을 사용하여 구할 수 있는 통계값 중 하나입니다.
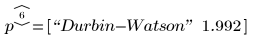
정규성 확인
표준화된 잉여값의 정규 도표를 만들어 Data 집합이 정규 분포해 있는지 확인합니다.
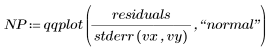
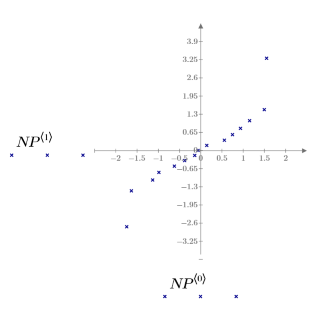
정규 도표가 직선에 가깝습니다. 따라서 오차가 대체로 정규 분포해 있다고 판단할 수 있습니다. 정규 도표는 오차 분산이 동일하지 않은 경우 등과 같이 가정에 반하는 다른 요소가 있을 때 민감하게 반응하므로 정규성을 최종 확인하기에 적합합니다.