예제: 유리 함수 회귀 2

rationalfitnp - 극점 없음

rationalfit 및 rationalfitnp 함수를 사용하여 유리 함수 회귀를 수행합니다. rationalfit 함수 대신 rationalfitnp 함수를 사용하는 경우 일반적인 최소자승 문제의 해를 조사하여 적합 구간 내에 분모의 근이 있는지 확인합니다. 극점이 없으면 생성된 적합식을 반환하고, 극점이 있으면 비선형 최적화 문제에 다른 제약 조건을 더 추가합니다.

1. x의 역함수를 조금 수정하여 데이터 집합을 정의합니다.

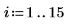
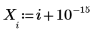
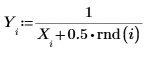
2. 유리 함수 분자와 분모의 차수를 지정합니다.

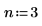
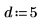
적합식의 형식은 다음과 같습니다.

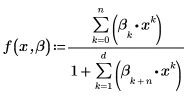
3. 신뢰 한계를 정의하고 표준 편차의 벡터를 정의합니다.

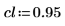
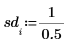
4. rationalfit 및 rationalfitnp 함수를 호출합니다.

<region id="ID0ERQZS" top="710.40000000000009" left="38.400000000000006" height="27.752000000000002" width="307.8966666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="136">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">param1</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rationalfit</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">cl</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">d</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">sd</id>
          <apply>
            <pow />
            <real>10</real>
            <real>-5</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EARZS" top="748.80000000000007" left="38.400000000000006" height="27.752000000000002" width="325.19" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="138">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">param2</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rationalfitnp</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">cl</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">d</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">sd</id>
          <apply>
            <pow />
            <real>10</real>
            <real>-5</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

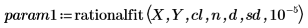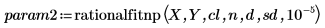param1 및 param2의 첫째 열에는 매개변수가 포함되고 나머지 열에는 앞서 정의한 신뢰 한계의 각 매개변수에 대한 하한 및 상한 경계가 포함됩니다.

5. 데이터 집합과 회귀 곡선 두 개를 도표화합니다.

<region id="ID0E6TZS" top="1420.8000000000002" left="38.400000000000006" height="27.752000000000002" width="171.18" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="144">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <apply>
            <matcol />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">param1</id>
            <real>0</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ENUZS" top="1459.2000000000003" left="38.400000000000006" height="27.752000000000002" width="188.97" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="146">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fitnp</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <apply>
            <matcol />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">param2</id>
            <real>0</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E2UZS" top="1747.2000000000003" left="19.200000000000003" height="350.4" width="594.60000000000059" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="148">
          <traceStyle color="#FFFF0000" symbol="filledRectangle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="149" num-of-points="500">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="150" num-of-points="500">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="456.200000000001" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="86.1333333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="155">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">X</id>
              </math>
              <math resultRef="156">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="157">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="158">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="152">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="154">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="110.99" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="163">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Y</id>
              </math>
              <math resultRef="164">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="165">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">fit</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </math>
              <math resultRef="166">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="167">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">fitnp</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </math>
              <math resultRef="168">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="160">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="162">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

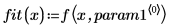
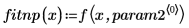
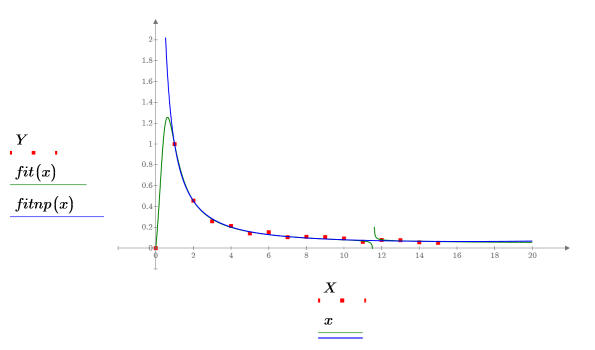
rationalfitnp 함수를 통해 극점이 제거되었습니다. 분모 다항식은 다음 형식으로 계산됩니다.

<region id="ID0ERVZS" top="2246.4000000000005" left="38.400000000000006" height="80.4" width="415.5333333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="183">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <id xml:space="preserve">denom</id>
        <id xml:space="preserve">x</id>
      </apply>
      <apply>
        <mult />
        <apply>
          <product />
          <lambda>
            <boundVars>
              <id xml:space="preserve">i</id>
            </boundVars>
            <parens>
              <apply>
                <plus />
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <apply>
                      <indexer />
                      <id xml:space="preserve">a</id>
                      <id xml:space="preserve">i</id>
                    </apply>
                    <apply>
                      <pow />
                      <id xml:space="preserve">x</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <apply>
                      <indexer />
                      <id xml:space="preserve">b</id>
                      <id xml:space="preserve">i</id>
                    </apply>
                    <id xml:space="preserve">x</id>
                  </apply>
                </apply>
                <apply>
                  <indexer />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve">i</id>
                </apply>
              </apply>
            </parens>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <id xml:space="preserve">floor</id>
              <apply>
                <div />
                <id xml:space="preserve">n</id>
                <real>2</real>
              </apply>
            </apply>
          </upperBound>
        </apply>
        <apply>
          <product />
          <lambda>
            <boundVars>
              <id xml:space="preserve">i</id>
            </boundVars>
            <parens>
              <apply>
                <plus />
                <apply>
                  <mult />
                  <apply>
                    <indexer />
                    <id xml:space="preserve">b</id>
                    <id xml:space="preserve">i</id>
                  </apply>
                  <id xml:space="preserve">x</id>
                </apply>
                <apply>
                  <indexer />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve">i</id>
                </apply>
              </apply>
            </parens>
          </lambda>
          <lowerBound>
            <apply>
              <id xml:space="preserve">floor</id>
              <apply>
                <div />
                <id xml:space="preserve">n</id>
                <real>2</real>
              </apply>
            </apply>
          </lowerBound>
          <upperBound>
            <apply>
              <minus />
              <apply>
                <mult />
                <real>3</real>
                <apply>
                  <id xml:space="preserve">floor</id>
                  <apply>
                    <div />
                    <id xml:space="preserve">n</id>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
              <id xml:space="preserve">n</id>
            </apply>
          </upperBound>
        </apply>
      </apply>
    </apply>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

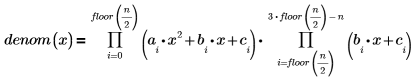
극점을 없애기 위해 다음 제약 조건이 추가되었습니다.

<region id="ID0EZXZS" top="2534.4000000000005" left="38.400000000000006" height="47.2" width="130.51999999999998" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="191">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">i</id>
      <apply>
        <minus />
        <apply>
          <mult />
          <real>3</real>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">floor</id>
            <apply>
              <div />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

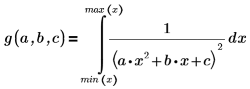
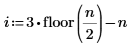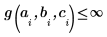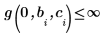LeastSquaresFit

rationalfitnp 및 LeastSquaresFit을 사용하여 얻은 맞춤 곡선을 비교합니다. LeastSquaresFit 함수는 rationalfitnp의 경우와 같은 알고리즘을 수행하지만 매개변수에 대한 추측값과 신뢰 한계가 필요합니다. 상수 항을 분모가 아니라 분자에 사용하려는 경우에 이를 수행할 수 있습니다.

1. 적합식을 정의합니다.

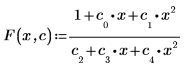
2. 매개변수에 대한 추측값을 정의합니다.

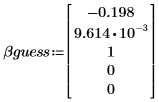
3. 매개변수에 대한 하한 및 상한 경계 조건을 정의합니다.

4. LeastSquaresFit 함수를 호출합니다.

<region id="ID0EOA1S" top="3187.2000000000003" left="38.400000000000006" height="27.752000000000002" width="448.2233333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="201">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">param3</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">LeastSquaresFit</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">X</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">F</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">βguess</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">cl</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">sd</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Bounds</id>
          <apply>
            <pow />
            <real>10</real>
            <real>-5</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

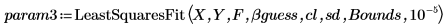
5. 데이터 집합과 rationalfitnp 및 LeastSquaresFit 함수를 통해 얻은 맞춤 곡선을 도표화합니다.

<region id="ID0EGC1S" top="3283.2000000000003" left="38.400000000000006" height="27.752000000000002" width="203.38666666666666" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="203">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">fitLSF</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">F</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <apply>
            <matcol />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">param3</id>
            <real>0</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EUC1S" top="3475.2000000000007" left="19.200000000000003" height="312" width="596.542857142857" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="205">
          <traceStyle color="#FFFF0000" symbol="filledRectangle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="206" num-of-points="500">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="207" num-of-points="500">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.942857142857" height="216" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="ticknumberlock" positionticmark="0" legendWidth="128.406666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="212">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">X</id>
              </math>
              <math resultRef="213">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="214">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="215">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="209">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="211">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="122.283333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="220">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Y</id>
              </math>
              <math resultRef="221">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="222">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">fitLSF</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </math>
              <math resultRef="223">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="224">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">fitnp</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </math>
              <math resultRef="225">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="217">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="219">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

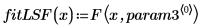
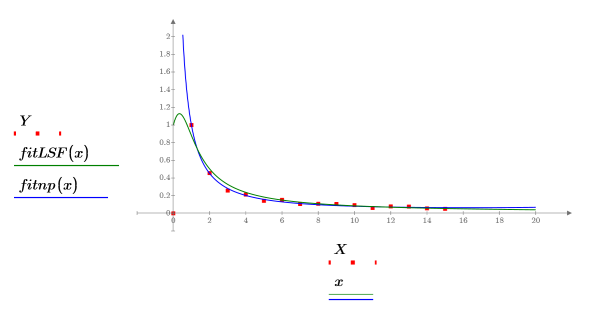
유리 함수 적합을 수행하기 전에 데이터를 직선에 가깝게 편향시키는 임의의 필터링 방법이나 데이터 변환 방법을 사용하면 rational 함수의 수렴 속도를 상당히 높일 수 있고 불필요한 극점을 제거하는 부수적인 효과도 얻을 수 있습니다.