예제: 유리 함수 회귀 1
rationalfit
rationalfit 함수를 사용하여 데이터에 유리 다항식을 맞춥니다.
1. 데이터 집합을 정의합니다.

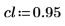
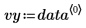
이 데이터 집합은 반도체 전자 이동도에 대한 NIST 연구에서 가져온 것입니다. 예측 변수 vx는 밀도의 자연 로그입니다. 응답 변수 vy는 전자 이동도를 측정한 값입니다.
2. 유리 함수 분자와 분모의 차수를 지정합니다.

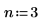
적합식의 형식은 다음과 같습니다.
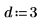
3. 신뢰 한계를 정의합니다.
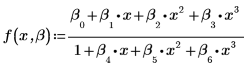
4. rationalfit 함수를 호출합니다.
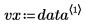
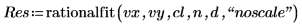
출력의 첫째 열에는 매개변수 값이 포함됩니다. 둘째 열과 셋째 열에는 신뢰 한계의 하한값과 상한값에 대한 출력이 각각 포함됩니다.
5. 매개변수의 값을 NIST 웹 사이트에 나와 있는 올바른 값과 비교합니다.


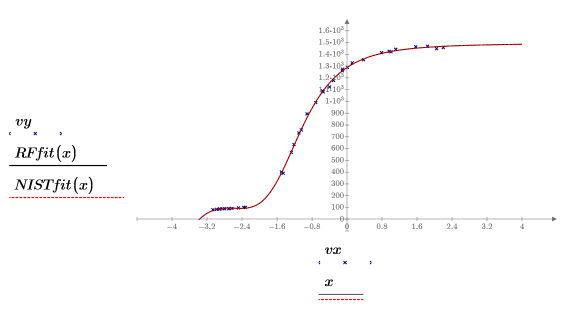
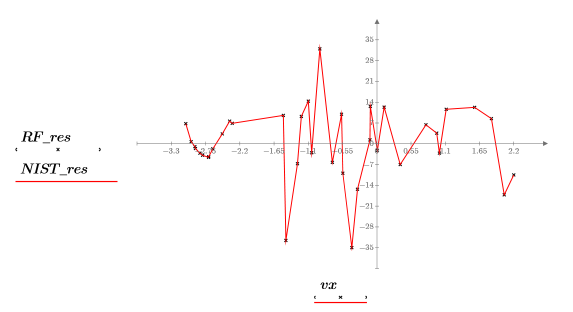
6. 데이터, 유리 함수 회귀 및 NIST 매개변수로 정의한 적합식을 도표화합니다.

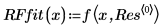
상관 계수에서 알 수 있듯이 유리 함수 회귀의 적합도가 거의 완벽합니다.
잉여 도표
위의 회귀에 대한 적합식이 얼마나 잘 들어맞는지 보여 주는 잉여 도표를 만듭니다.
1. 자유도를 정의합니다.
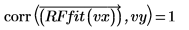
2. 잉여값을 계산합니다.
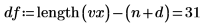
3. 잉여값 제곱의 합을 계산합니다.
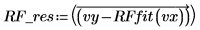
4. 표준 편차를 계산합니다.
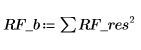
5. NIST 웹 사이트에 나와 있는 값을 사용하여 2-4단계를 반복합니다.
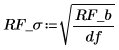
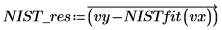
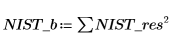
6. 두 적합의 결과를 비교합니다.
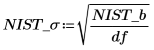
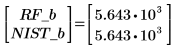
7. 데이터 점과 잉여값을 도표화합니다.
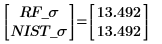
제약 조건, 표준 편차 및 공차
rationalfit에는 표준 편차 벡터, 하한계 및 상한계 행렬, 정밀도, "배율 없음(noscale)" 등과 같은 여러 가지 선택적 인수를 사용할 수 있습니다. 이러한 선택적 인수를 단독으로 사용할 수도 있지만, 위에 정의된 처음 세 개의 인수에 대해서는 인수의 순서가 중요합니다.
1. 매개변수에 대한 하한계와 상한계로 이루어진 행렬을 만듭니다.
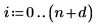
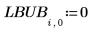
2. 매개변수의 표준 편차로 이루어진 벡터를 만듭니다.
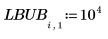
표준 편차의 벡터를 rationalfit 함수에 대한 인수로 입력하면 풀이를 통해 다음 함수가 최소화됩니다.
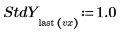
특정 점에서 표준 편차가 0이면 편차 없는 원래 함수가 해당 점에 사용됩니다. 즉, StdYi가 1로 설정됩니다.
3. 정밀도를 설정합니다. 기본값은 10-7입니다.
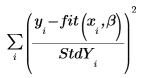
4. 4. rationalfit 함수를 호출합니다. 함수를 호출하여 얻은 매개변수 값을 NIST 웹 사이트에 나와 있는 올바른 값과 비교합니다.
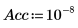
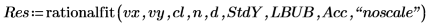
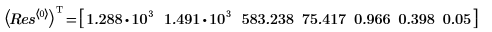
rationalfit 함수는 입력 데이터에 대해 자동 배율 조정을 수행하므로 배율이 달라지더라도 정밀도를 계속 유지할 수 있습니다. 이 함수는 원래 데이터에 맞춰 출력 매개변수의 배율을 다시 조정합니다. 따라서 대부분의 경우 입력 데이터의 상대적 배율에 상관없이 올바른 적합을 얻을 수 있습니다. 제대로 된 적합을 구하는 데 문제가 있으면 인수 목록의 맨 끝에 “noscale” 옵션 문자열을 추가하여 이 옵션을 해제합니다.