예제: 적합도
polyfit 및 polyfitstat 함수로 선형 회귀와 분산분석을 수행하여 적합도를 검사합니다.
1. 폴리머 공정에 대한 실험 데이터가 포함된 표를 정의합니다. 반응 온도 t와 촉매 주입률 fr이 폴리머의 점도 vy에 영향을 줍니다.

적합도
2. polyfit 함수를 호출하여 데이터를 선형 회귀로 모델링합니다.
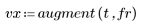
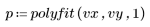
3. 온도 및 주입률 설정 각각에 대해 예측한 점도를 계산합니다.
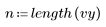
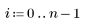
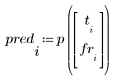
4. 잉여값(Residual), 즉 계산을 통해 구한 모델 값과 측정한 값 사이의 차이를 구합니다.
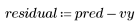
5. 관측한 점도, 온도 및 주입률을 기준으로 잉여값을 도표화합니다.
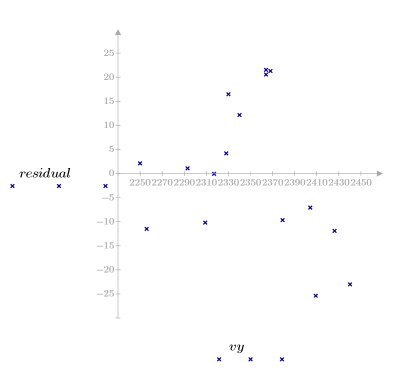
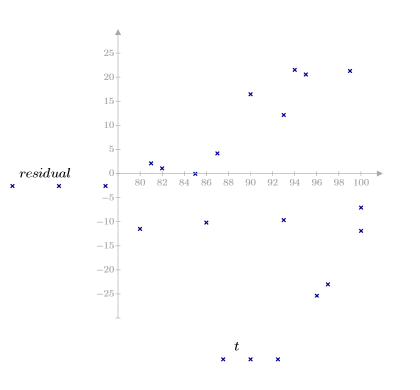
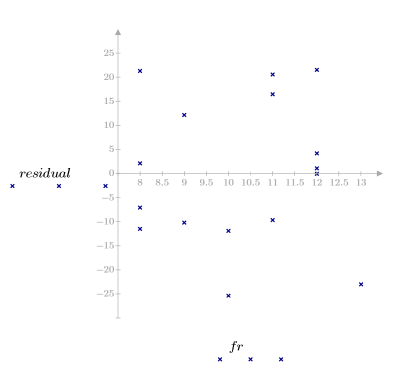
잉여 도표를 보면 점도와 온도가 올라갈수록 점도 관측값과 온도의 분산도 각각 증가하는 것으로 나타납니다.
6. polyfitstat을 호출하여 선형 모델에 대한 여러 가지 통계값을 구합니다. polyfitstat로 구한 분산분석 행렬을 행 8에 표시합니다.
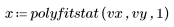
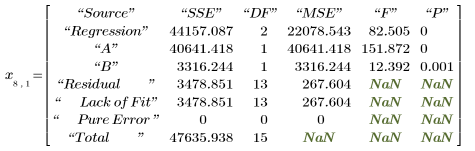
분산분석 행렬에서 분산 소스는 회귀(Regression) 및 잉여(Residual) 컴포넌트로 나뉩니다. 회귀 컴포넌트는 다시 각 회귀 계수로 추가 분할됩니다. 그러나 실험 결과 vy에는 반복측정치가 없으므로 잉여값의 적합도가 낮은 경우와 순수한 오차가 발생한 경우를 구분할 수는 없습니다.
회귀에 대한 분산분석 표 계산 및 사용
1. 오차에 따른 제곱합(SSE)을 구합니다.
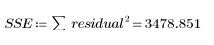
SSE는 적합도에 대한 일반적인 척도인 χ2과 같습니다. 이는 최소자승 해를 구할 때 최소화되는 수량입니다. 오차는 모델이 데이터에 얼마나 잘 들어맞는지를 측정한 값으로, 회귀를 통해 설명할 수 없는 편차의 크기를 나타냅니다.
2. 전체 자유도 df_total 및 매개변수 df_param의 자유도를 기준으로 오차 df_error의 자유도를 정의합니다. 자유도는 적합 매개변수의 수를 뺀 데이터의 길이입니다.
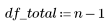
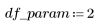
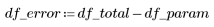
3. 총 제곱합(SST)을 기준으로 회귀에 따른 제곱합(SSR)을 정의합니다.
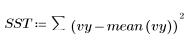
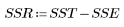
4. 평균 제곱 오차(MSE)와 회귀 평균 제곱(MSR)을 정의합니다. 오차를 적절한 자유도로 나눕니다.
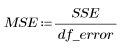
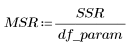
5. 적합식의 특징을 보여 주는 분산분석 표를 작성합니다.
제곱합 | DF | 평균 제곱 | F 인수 | |
|---|---|---|---|---|
회귀 | 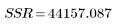 | 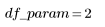 | 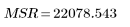 | 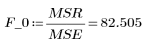 |
오차 | 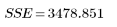 | 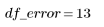 | 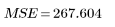 | |
총 | 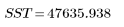 | 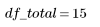 |
위의 표를 polyfitstat 분산분석 행렬과 비교할 수 있습니다.
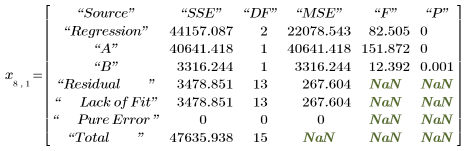
6. 모델이 데이터에 얼마나 잘 들어맞을지 추정합니다.
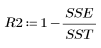
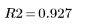
이 결과는 점도 변동의 92.7%가 선형 회귀 모델로 설명될 수 있음을 의미합니다.
7. 모델이 데이터에 잘 들어맞는지 검사하는 가설 검정에 대한 유의 수준을 정의합니다.
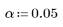
8. 임계 F 값을 계산합니다.
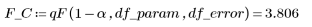
9. 모델이 데이터에 잘 들어맞는다는 가설을 검정합니다.
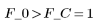
가설을 받아들입니다. 이 선형 회귀 모델을 사용하여 폴리머의 점도를 예측할 수 있습니다.
참조
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001년, 페이지 398