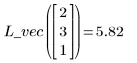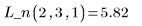예제: 조각 2차 적합
일변수 다항식 회귀
loess 함수로 국소 회귀를 사용하여 데이터에 일련의 2차 함수를 맞춥니다.
1. 다음 행렬을 정의합니다.

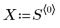
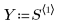
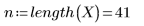
2. 각 데이터 점 주위의 가중치 창에 있는 점의 총 개수를 백분율로 나타낸 값인 거리를 정의합니다. 이 값은 loess 함수에서 연속 2차 적합을 구하는 데 사용됩니다.
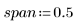
일반적으로 (span*n)이 1보다 커야 합니다. 1보다 큰 점의 개수를 각각의 최소자승 가중 적합식으로 평균을 낼 것이기 때문입니다.
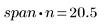
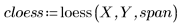
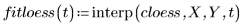
4. polyfit 함수를 호출하여 데이터 집합에 2차 다항식을 맞춥니다.
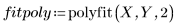
5. 위에서 정의한 곡선 두 개를 도표화합니다.
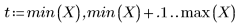
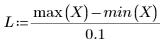
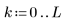
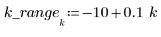
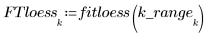
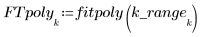
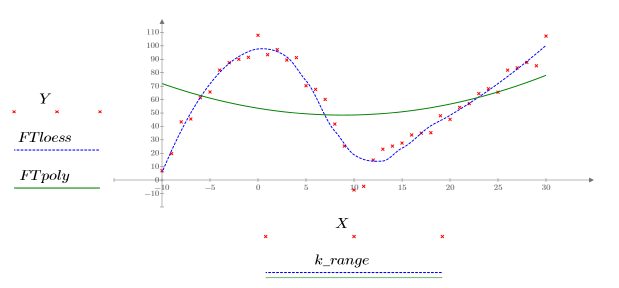
• 거리가 2나 3 정도로 크면 데이터가 거의 동일한 가중치를 갖는 단일 2차 적합인 것으로 간주됩니다. 적합식이 2차 다항식의 polyfit 해에 근접합니다.
• 거리를 선택하는 데는 사실상 정확한 지침이 없습니다. 거리가 클수록 적합식에서 연결되는 조각의 수가 줄어들므로 loess 적합식의 도표가 더 매끄럽게 표현됩니다. 그러나 이 경우 적합식이 데이터의 특징을 제대로 반영하지 못할 수 있습니다. 반대로 거리가 작으면 loess가 수렴하지 않을 수 있습니다.
• loess 알고리즘은 외삽법에 사용하기 위해 설계된 것이 아닙니다. 원래 X 범위를 벗어난 값에서 interp를 계산하려고 하면 오류가 발생합니다.
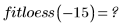
• 데이터에 다소간 불연속 특징이 있지만 수동으로 조각을 맞추고 싶지 않거나 물리적으로 비현실적인 복소수 또는 비선형 적합 방법을 사용하고 싶지 않은 경우에 loess를 사용할 수 있습니다.
다변수 다항식 회귀
loess 함수를 사용하여 다변수 다항식 회귀를 수행합니다. loess 함수로 맞출 수 있는 독립 변수는 네 개까지입니다.
1. 데이터 집합을 정의합니다.
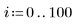
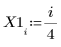
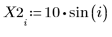
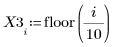
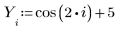
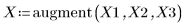
2. 평활 매개변수를 정의합니다.
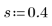
이 매개변수는 인수가 한 개일 때와 의미가 같습니다.
3. loess 함수를 호출합니다.
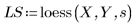
4. interp를 호출하여 다변수 적합식을 보간합니다. 적합식에 n개의 요소로 이루어진 벡터를 사용하거나 n개의 인수로 구성된 집합을 사용할 수 있습니다. 여기서 n은 독립 인수의 개수입니다.
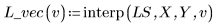
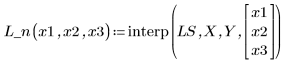
5. 적합식을 사용하여 점 (2, 3, 1)에서 Y의 값을 예측합니다.