예제: 비선형 회귀 2
LeastSquaresFit 함수를 사용하여 비선형 회귀를 수행합니다. LeastSquaresFit 풀이를 사용하면 비선형 회귀 문제를 매우 유연하게 풀 수 있습니다. 예를 들어 임의의 종속 매개변수에 대한 제약 조건 방정식, 매개변수의 하한계와 상한계, x 값에 대한 표준 편차, 계산의 신뢰 한계 등을 입력할 수 있습니다.
LeastSquaresFit
1. 데이터 집합을 정의합니다.
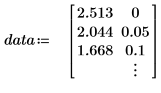
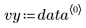
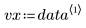
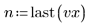
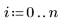
이 데이터는 NIST 웹 사이트에 설명되어 있는 예제에서 가져왔습니다. 데이터를 생성하는 데는 다음 방정식이 사용되었으며 정밀도는 14자리입니다.
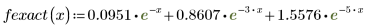
2. 적합식을 정의합니다.
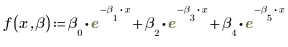
위의 개별 매개변수는 벡터 β의 요소입니다. 벡터의 요소 대신 개별 변수 이름을 사용하여 입력 함수를 지정할 수도 있습니다.
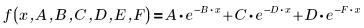
3. 추측값을 입력합니다.
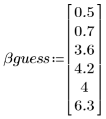
4. 매개변수에 대한 신뢰 한계를 정의합니다.
5. LeastSquaresFit 함수를 호출합니다.
이 풀이에서 최소자승 문제 결과를 푸는 데는 SQP(순차 2차 계획법)이 사용됩니다. 변수를 추가로 도입하여 원래 문제를 일반 등호 제약 조건의 비선형 계획법 문제로 변형했습니다. 이렇게 하면 일반적으로 다른 방법을 사용할 때보다 더 빠르고 더 안정적으로 문제를 풀 수 있습니다.
6. LeastSquaresFit 함수를 사용하여 구한 출력 벡터를 검토합니다.
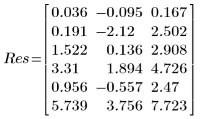
◦ 출력의 첫째 열에는 적합식 매개변수의 값이 포함됩니다. 둘째 열에는 매개변수에 대한 신뢰 구간의 왼쪽 경계가, 셋째 열에는 오른쪽 경계가 포함됩니다.
◦ 매개변수의 신뢰 한계 95%에 상당히 넓은 범위가 포함됩니다. 이는 맞춤이 쉽지 않고 개별 매개변수가 매우 다양할 수 있음을 의미합니다. 따라서 적합식 매개변수의 값과 NIST 웹 사이트에 기록된 올바른 값 사이에 차이가 있습니다.
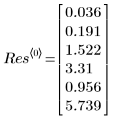

7. 데이터, 최소자승 적합식 및 NIST 적합식을 도표화합니다.
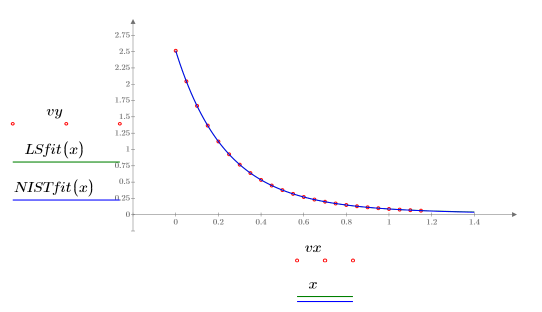
8. 최소자승 적합식을 원래 데이터와 비교합니다.
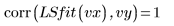
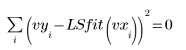
적합식이 수렴에 근접하고 있지만 수렴 허용 오차(CTOL)를 조정하여 더 나은 결과를 얻을 수도 있습니다. 이를 위해서는 LeastSquaresFit 함수의 선택적 인수 중 하나를 조정하면 됩니다.
제약 조건, 표준 편차 및 공차
LeastSquaresFit에는 다음과 같은 여러 가지 선택적 인수를 사용할 수 있습니다.
• 표준 편차 벡터
• 하한계 및 상한계 행렬
• 정밀도
이러한 선택적 인수를 단독으로 사용할 수도 있지만, 만일 둘 이상의 인수를 입력하는 경우에는 인수의 순서가 중요합니다.
1. 데이터 값 중 하나를 교란하여 잘못된 측정을 시뮬레이트합니다.
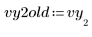
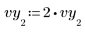
2. 하한계와 상한계를 지정하여 적합 값에 대한 제약 조건을 설정합니다.
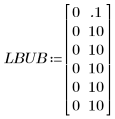
이 예제의 경우에는 특정 경계가 알려져 있지 않으므로 예상되는 매개변수 값을 충분히 벗어난 지점에 경계가 설정됩니다.
3. 각 y 값에 대한 표준 편차의 벡터를 설정하여 이상치를 마스킹합니다.
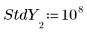
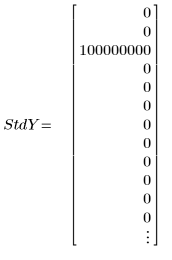
◦ 표준 편차의 값이 108 정도로 크면 사실상 측정이 올바르지 않다는 사실을 쉽게 발견하고 이를 계산에서 제외할 수 있습니다.
◦ 표준 편차의 벡터를 LeastSquaresFit 함수에 대한 인수로 입력하면 풀이를 통해 다음 함수가 최소화됩니다.
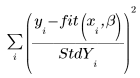
특정 점에서 표준 편차가 0이면 편차 없는 원래 함수가 해당 점에 사용됩니다. 즉, StdYi가 1로 설정됩니다.
4. 계산에 더 엄격한 수렴 허용 오차를 적용하기 위한 정밀도를 설정합니다. 기본값은 10-7입니다.
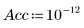
5. 한 번은 표준 편차를 사용하여, 또 한 번은 표준 편차를 사용하지 않고 LeastSquaresFit 함수를 호출합니다.
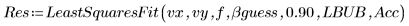
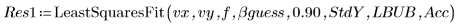
◦ 신뢰 한계가 너무 크기 때문에 마스킹하지 않은 계산은 실패합니다.
◦ 새 매개변수는 NIST 값에 좀 더 근접합니다.
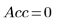
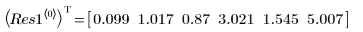
6. 이상치와 마스킹한 적합식을 사용하여 데이터를 도표화합니다.
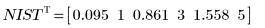
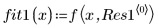
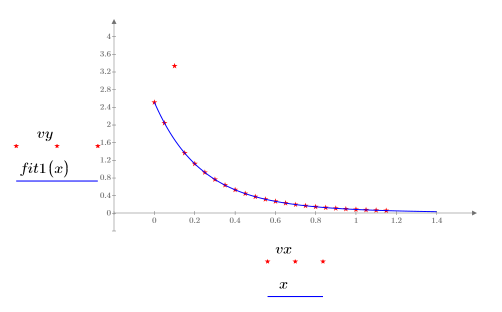
참조
이 예제의 데이터 출처: Lanczos, C., Applied Analysis, Prentice Hall, 1956년, 272-280페이지. 이 문서는 NIST Statistical Reference Dataset Archive에 게시되어 있습니다.