예제: LU 행렬 인수 분해
LU 함수를 사용하여 LU 행렬 인수 분해를 수행합니다.
|
|
부울 비교를 수행할 때 논리적 불일치를 피하려면 계산 옵션 드롭다운 목록에서 근사 등호를 활성화합니다.
|
실수 행렬의 LU 인수 분해
1. 치수 m x n(m > n)인 실수 행렬 M1을 정의합니다.
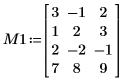
2. LU 함수를 사용하여 행렬 M1의 LU 행렬 인수 분해를 수행합니다.

3. P1 x M1 = L1 x U1임을 보여줍니다.
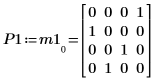 |  | 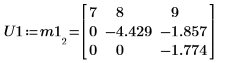 |
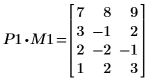 | 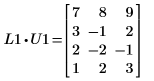 | |
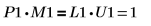 |
관계는 논리적으로 참입니다.
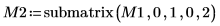 |
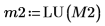 |
5. P2 x M2 = L2 x U2임을 보여줍니다.
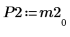 | 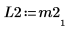 | 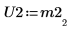 |
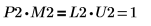 |
관계는 논리적으로 참입니다.
6. submatrix 함수를 사용하여 m = n인 행렬 M3를 추출합니다.
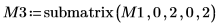 |
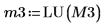 |
7. P3 x M3 = L3 x U3임을 보여줍니다.
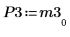 | 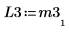 | 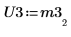 |
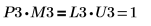 |
관계는 논리적으로 참입니다.
복소수 행렬의 LU 인수 분해
1. 치수 m x n(m > n)인 복소수 행렬 C1을 정의합니다.
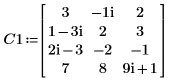
2. LU 함수를 사용하여 행렬 C1의 LU 행렬 인수 분해를 수행합니다.

3. P4 x C1 = L4 x U4임을 보여줍니다.
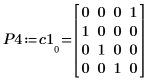 | 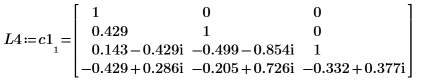 | 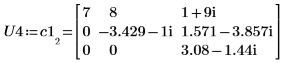 |
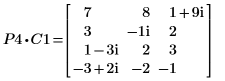 | 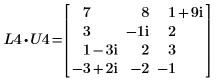 | |
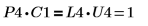 |
관계는 논리적으로 참입니다.
4. submatrix 함수를 사용하여 m < n인 행렬 C2를 추출합니다.
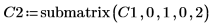 | 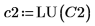 | 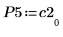 |
5. P5 x C2 = L5 x U5임을 보여줍니다.
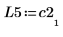 | 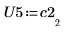 |
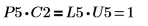 |
관계는 논리적으로 참입니다.
6. submatrix 함수를 사용하여 m = n인 행렬 C3를 추출합니다.
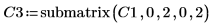
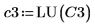
7. P6 x C3 = L6 x U6임을 보여줍니다.
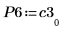 | 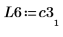 | 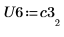 |
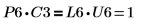 |
관계는 논리적으로 참입니다.