예제: 위치 예측 함수
mean, median, mode 및 percentile 함수를 사용하여 나머지 분포를 기준으로 하는 데이터 점의 상대 위치를 측정합니다. 가장 적합한 위치 예측 함수는 데이터의 일반 분산 또는 분포에 따라 결정됩니다.
mean
데이터 집합의 산술 평균을 구합니다.
1. 수치 데이터의 집합을 정의합니다.

2. mean 함수를 사용하여 데이터의 산술 평균을 계산합니다.
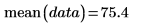
이는 다음 계산과 동일합니다.
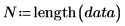
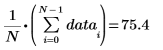
3. 데이터 점 중 하나를 변경한 후 평균을 다시 계산합니다.
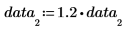
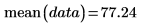
데이터 점 중 하나 이상의 값이 변경되면 평균에 영향을 미칩니다. 데이터 집합에 중대한 이상치가 있으면 평균이 중심 위치를 제대로 나타내지 못합니다. 이 경우 이상치를 트림하고 트림된 평균을 계산하면 더 나은 추정 결과를 얻을 수 있습니다.
median
데이터 집합의 중앙값 또는 가운데 값을 구합니다.
1. median 함수를 사용하여 이전 데이터 집합의 중앙값을 구합니다.
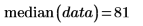
2. sort 함수를 사용하여 데이터를 오름차순으로 정렬하고 중앙값이 집합의 중간 값임을 보여줍니다.
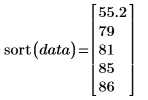
중앙값은 모든 데이터 점의 실제 값이 아니라 데이터의 상대적 위치에 따라 결정됩니다. 따라서 중앙값은 개별 데이터 값이 약간 변경되더라도 비교적 영향을 덜 받습니다.
3. median 함수를 사용하여 짝수 개의 데이터 점에 대한 중앙값을 구합니다.
 | 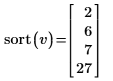 | 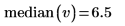 |
데이터 집합에 짝수 개의 데이터 점이 있는 경우 가운데 있는 두 데이터 점의 평균이 중앙값이 됩니다.
mode
데이터 집합의 모드는 최고주파에서 발생하는 값입니다.
1. mode 함수를 사용하여 데이터 집합의 모드를 구합니다. 데이터에 반복되는 값이 없기 때문에 오류가 반환됩니다.


2. 같은 주파수가 반복되는 두 개 이상의 요소가 포함된 새 데이터 집합을 생성합니다.
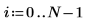 | 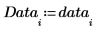 | 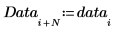 |
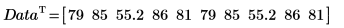 | ||
3. mode 함수를 사용하여 두 개 이상의 데이터 값이 같은 주파수로 반복될 경우 오류가 반환됨을 보여줍니다.

percentile
percentile 함수를 사용하여 데이터 집합의 백분위수, 사분위수 및 중앙값을 구합니다. 백분위수는 데이터 집합에서 총 점 수의 특정 백분율 이하인 값을 측정합니다.
1. 데이터 집합을 정의합니다.
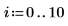
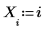
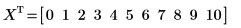
2. percentile 함수를 사용하여 데이터 집합 X의 50번째 백분위수를 구합니다.
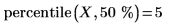
이 값은 데이터 집합 X의 중앙값에 해당합니다.
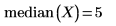
3. percentile 함수를 사용하여 데이터 집합 X의 90번째 백분위수를 구합니다.
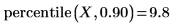
90번째 백분위수는 두 데이터 점 사이에서 발생합니다.
4. percentile 함수를 사용하여 첫 번째 데이터 집합의 사분위수를 구합니다.
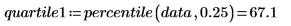
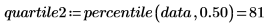
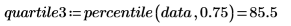
사분위수는 데이터의 1/4을 표시하는 3개의 백분위수 중 하나입니다. 사분위수는 변위치-변위치 도표에서 데이터의 그래프 분석에 사용됩니다.