예제: 선형 예측법
burg 및 yulew 함수를 사용하여 잘 알려진 선형 예측 모델에 대한 계수를 생성합니다. 이러한 함수는 각각 Burg 방법과 율-워커 알고리즘을 구현합니다. 이 알고리즘과 수학적 원리에 대한 설명은 Sophocles J. Orfanidis의 Optimum Signal Processing(Macmillan, 1989년)을 참조하십시오.
율-워커 예측
1. cos 함수를 사용하여 코사인 신호를 정의합니다.
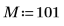
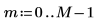
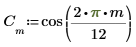
2. 신호를 도표화합니다.
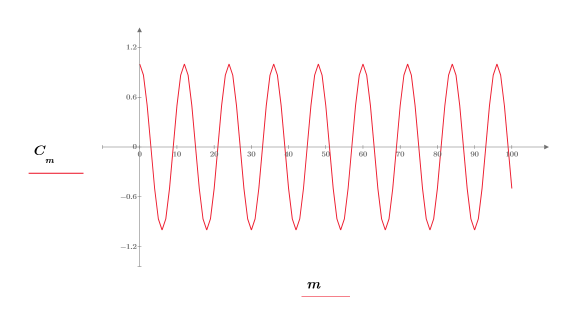
3. rnd 함수를 사용하여 신호에 임의 노이즈를 추가합니다.
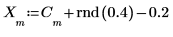
4. 원래 신호와 노이즈가 추가된 신호를 도표화합니다.
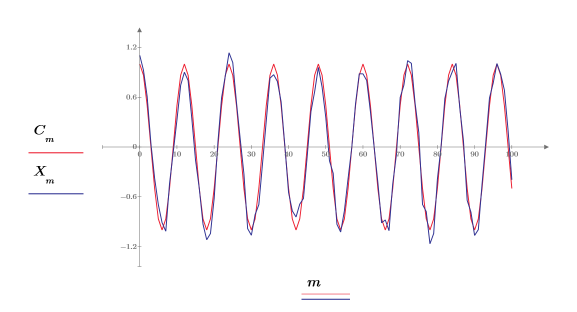
난수 컴포넌트가 진폭 0을 중심으로 가운데에 오도록 신호에서 0.2를 뺍니다.
5. 신호의 시작 부분에서 짧은 표본 집합을 가져옵니다.
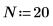
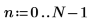
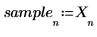
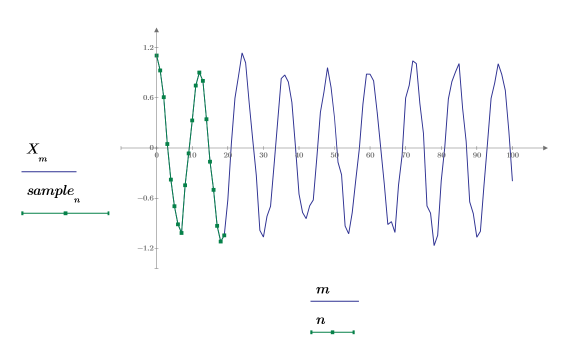
6. 예측 차수를 설정하고 yulew 함수를 사용하여 계수를 계산합니다.
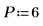
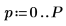

◦ 이러한 계수는 원래 신호를 근사화하는 전체 극점 필터에 대한 것입니다. 예상과 같이 코사인을 나타내는 큰 극점 하나와 노이즈를 근사화하는 작은 극점 여러 개가 있습니다.
◦ 차수 P는 시퀀스의 다음 값을 예측하는 데 사용되는 연속 값의 수를 결정합니다. 계수 벡터의 1번째부터 6번째까지의 요소가 사용되고 항상 1인 0번째 요소는 무시됩니다. 이 1은 y가 예측 오차의 전체 집합을 생성하는 예측 오차 필터로 사용될 때 필요합니다.
7. 이전의 P개 점을 사용하여 계산한 예측 점을 원래 데이터와 비교합니다. 이것은 신호 X 대신에 필터를 사용하는 것이 얼마나 정확한지 보여줍니다.
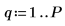
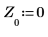
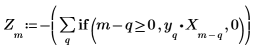
8. 원래 신호와 예측된 신호를 도표화합니다.
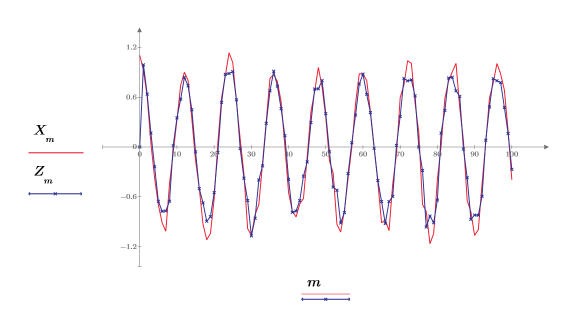
데이터의 첫 20개 점만 사용했지만 근사화는 매우 훌륭합니다.
9. response 함수를 사용하여 필터로 계수 배열을 사용한 다음 표본을 입력으로 사용하는 응답을 계산하여 율-워커 계수의 예측 오차를 생성합니다.
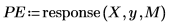
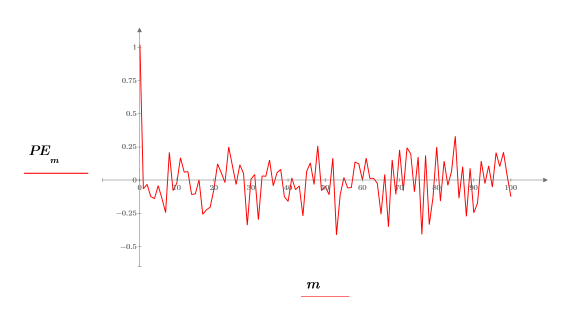
전체 계수 배열을 예측 오차 필터라고도 합니다.
10. 이러한 오차가 이전 두 도표와 차이가 있는지 확인합니다.
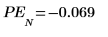
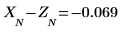
율-워커 알고리즘은 예측 오차 제곱의 합을 최소화합니다.
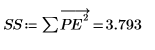
11. y를 교란(첫 번째 계수를 제외한 모든 계수에 작은 난수를 추가)한 후 합계를 다시 계산하여 최소화를 임의 확인합니다. 커서를 아래의 rnd 함수 위로 이동하고 [F5] 키를 몇 번 누릅니다.
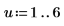
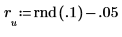
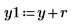
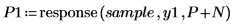
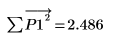
Burg 예측
1. 선형 예측이 잘 작동하는 시퀀스(알려진 계수의 자동 회귀 프로세스)를 구성합니다.
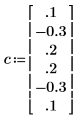
2. 시계열을 초기화합니다.
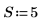
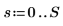
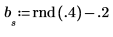
3. 자동 회귀와 노이즈를 사용하여 나머지 계열을 생성합니다.
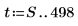
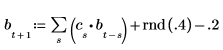
4. 전체 급수를 표본으로 사용하여 6차 모델에 대한 계수를 계산한 다음 burg 함수를 사용하여 계수를 계산합니다.
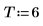
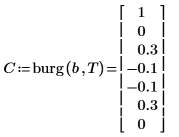
5. 이 문서의 부호 규약을 사용하여 실제로 프로세스를 생성한 계수를 비교합니다.
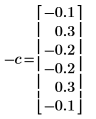
◦ 0차 계수는 항상 1이기 때문에 제외되었습니다.
◦ C의 계산된 요소 1 및 5가 다릅니다.
6. Burg 계수 벡터 C를 사용하여 예측 오차를 생성합니다.
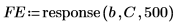
◦ Burg 방법은 첫 번째 P 오차에 0 가중치를 할당하므로 표본에 0을 채우는 것은 최소화에 영향을 미치지 않습니다. 이것은 율-워커로 수행된 최소화와 마찬가지입니다.
◦ 또한 Burg 조건에는 전향 오차 FE와 후향 오차 BE가 모두 포함됩니다.
7. response 및 reverse 함수를 사용하여 후향 오차를 계산합니다.
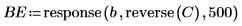
8. 예측 오차 FE와 자동 회귀 함수 b를 사용하여 실제 예측 AP를 계산한 다음 Pth번째 항부터 시작하여 예측 시리즈와 실제 시리즈를 도표화합니다.
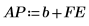
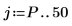
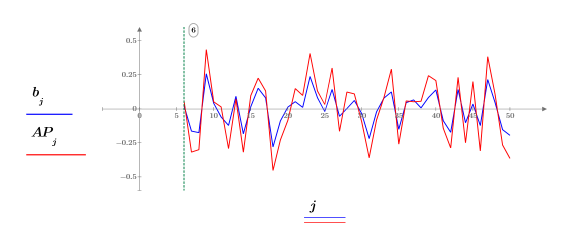
스펙트럼 예측
선형 예측 방법으로 생성된 계수를 사용하여 모델링하는 프로세스의 파워 스펙트럼을 예측합니다. 이 컨텍스트에서는 Burg 알고리즘을 최대 엔트로피 스펙트럼 분석(MESA: Maximum Entropy Spectrum Analysis)이라고 하며, 일부 경우 짧은 시계열의 스펙트럼을 FFT보다 훨씬 정확하게 결정합니다.
가우시안 노이즈가 추가된 싸인의 합으로 구성된 프로세스의 파워 스펙트럼을 예측합니다.
1. sin 함수를 사용하여 싸인 컴포넌트 두 개가 있는 신호를 정의합니다.
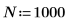
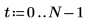
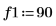
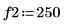
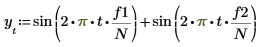
2. gaussn 함수를 사용하여 가우시안 노이즈를 추가합니다.
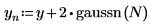
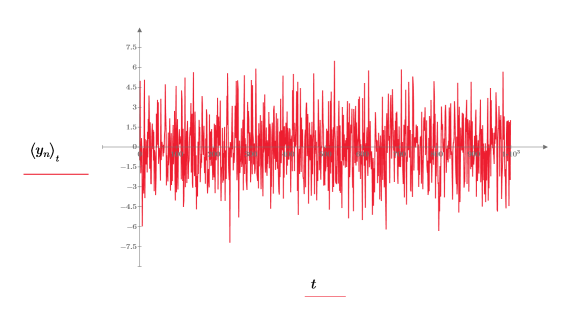
gaussn 함수는 평균 0이고 표준 편차 1인 가우시안 확률 분포에 따르는 난수로 구성된 n 요소 벡터를 구합니다.
3. 선형 예측을 위해 2차를 정의합니다.
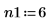
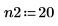
4. burg 함수를 사용하여 전체 급수를 표본으로 사용하는 2차 자동 회귀 모델의 스펙트럼을 추정합니다.
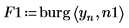
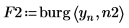
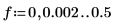

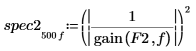
6. 두 파워 스펙트럼을 도표화합니다.
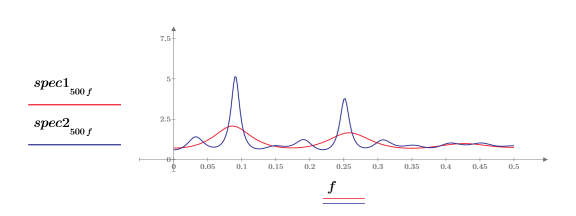
◦ 각 파워 스펙트럼에 두 개의 피크가 있습니다.
◦ 두 스펙트럼의 주파수 피크는 하한값뿐만 아니라 상한값도 동일한 주파수를 기준으로 발생합니다.
7. 게인 피크와 해당 발생 지점의 주파수를 쉽게 구할 수 있도록 spec1 및 spec2 곡선을 각각 두 개의 세그먼트로 분할합니다.
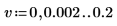 | 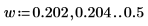 |
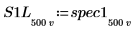 | 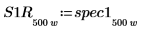 |
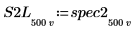 | 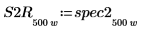 |
8. if 함수를 사용하여 지정된 세그먼트에서 피크 값을 갖는 주파수를 구하는 함수를 정의한 다음 이 함수를 사용하여 각 스펙트럼 그래프선의 좌변 및 우변 피크를 구합니다.
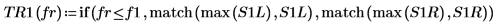 | |
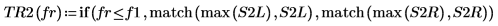 | |
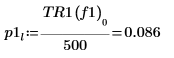 | 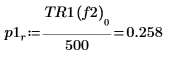 |
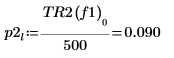 | 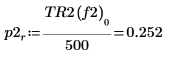 |
9. max 함수를 사용하여 각 피크의 크기를 계산합니다.
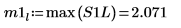 | 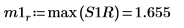 |
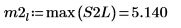 | 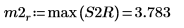 |
10. 각 함수를 개별적으로 도표화합니다. 가로 및 세로 마커를 사용하여 각 피크의 크기와 해당 발생 위치의 주파수를 표시합니다.
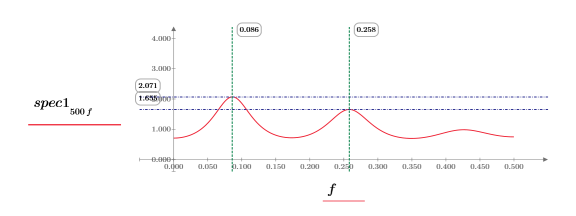
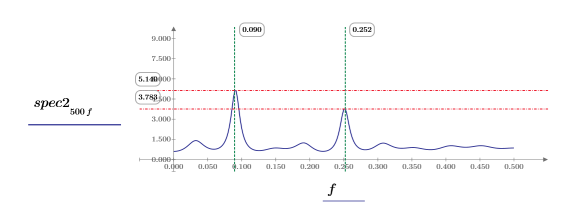
◦ 워크시트를 다시 계산하면서 두 도표를 관찰합니다.
◦ 피크의 크기가 다시 계산할 때마다 변하며 피크가 대개 서로 다른 값을 갖습니다. 하지만 크기가 동일할 수 있습니다.
◦ 피크는 거의 같은 주파수에서 발생합니다.
이 스펙트럼 예측 방법에 대한 자세한 내용은 S. Lawrence Marple, Jr.의 Digital Spectral Analysis with Applications(Prentice-Hall, Inc)를 참조하십시오.