예제: 켈빈 함수
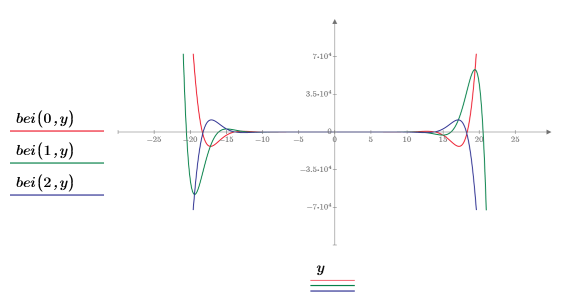
1. ber 및 bei의 0차 함수를 도표화합니다.
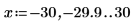
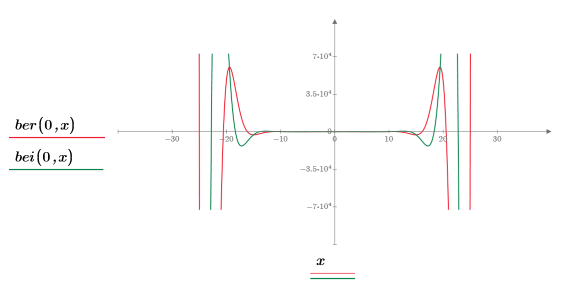
두 함수는 대칭으로 나타납니다.
2. 차수가 증가함에 따라 ber 및 bei 함수의 두 피크가 어떻게 변화하는지 보여주기 위해 X축을 확대하는 틱 표시 값을 재설정합니다.
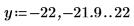
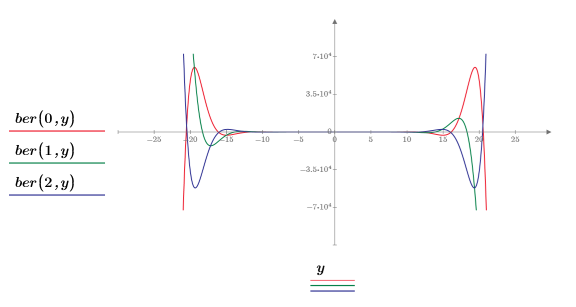
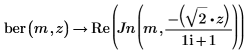
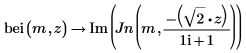
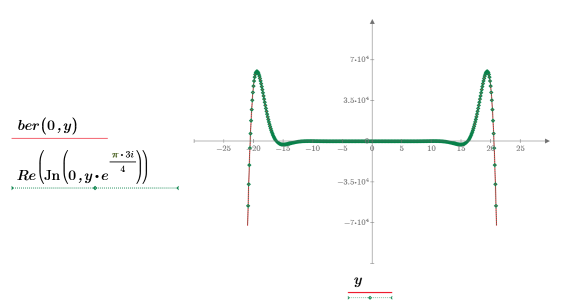
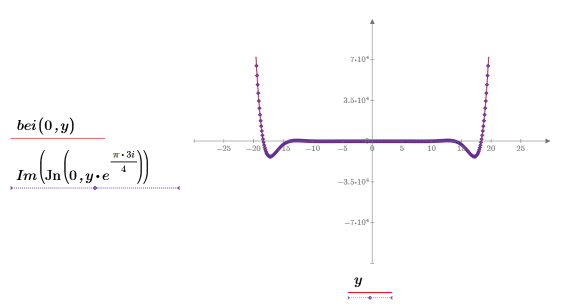
이 예제에서는 ber 함수만 보여주지만 bei 함수에도 같은 방법을 적용할 수 있습니다.
4. ber 함수를 사용하여 Z1 벡터를 정의합니다.
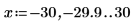
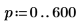
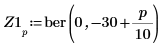
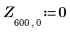
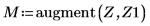
5. ber 함수의 국부적 최소값을 구합니다.

m=0인 경우 ber 함수의 최소값은 8개입니다. 이 함수는 대칭입니다. 고차 함수는 위치와 진폭에 따라 최소값 수가 달라집니다.
6. ber 함수의 국부적 최대값을 구합니다.

m=0인 경우 ber 함수의 피크는 7개입니다. 이 함수는 대칭입니다. 고차 함수는 위치와 진폭에 따라 최대값 수가 달라집니다.
7. 우변에 있는 네 개 최소값의 수직 좌표를 구합니다.
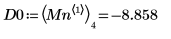
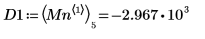
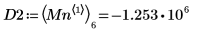
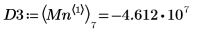
8. match 함수를 사용하여 일치하는 각 최소값의 지수를 구한 다음 동등한 수평 좌표를 구합니다.
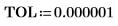
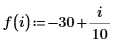
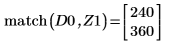
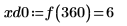
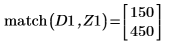
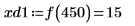
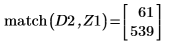
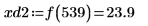
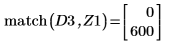
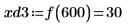
9. 우변에 있는 네 개 최대값의 수직 좌표를 구합니다.
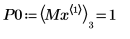
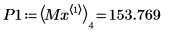
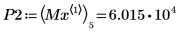
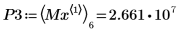
10. match 함수를 사용하여 일치하는 각 최대값의 지수를 구한 다음 동등한 수평 좌표를 구합니다.
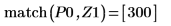
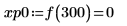
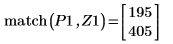
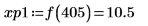
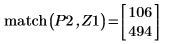
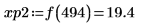
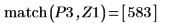
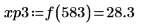
최대값과 최소값의 진폭 범위가 크게 변하기 때문에 한 도표에 이를 모두 표시하기 어려울 수 있습니다. |
11. 마커를 사용하여 첫 번째 최소값 (D0)과 첫 번째 최대값 (P0)을 표시합니다.
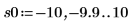
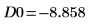
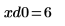
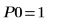
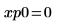
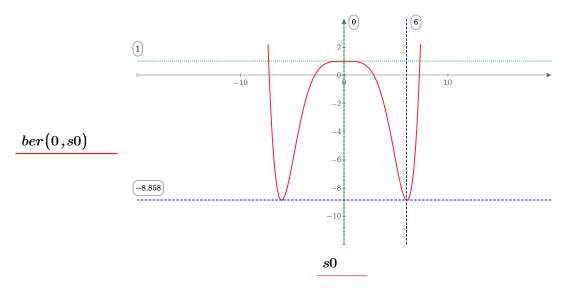
예상대로 그래프는 두 번째 최소값을 Y축 왼쪽에 보여줍니다.
12. 마커를 사용하여 다음 번 최소값 (D1)과 다음 번 최대값 (P1)을 표시합니다.
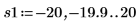
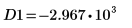
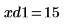
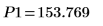
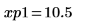
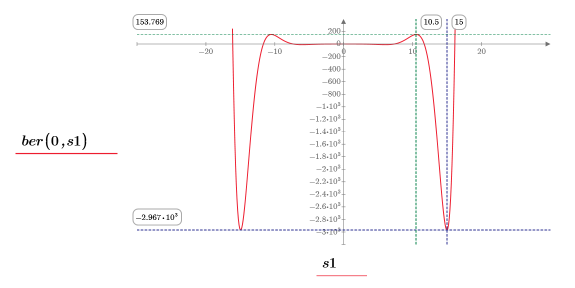
예상대로 그래프는 두 번째 최소값과 두 번째 최대값을 Y축 왼쪽에 보여줍니다.
13. 마커를 사용하여 다음 번 최소값 (D2)과 다음 번 최대값 (P2)을 표시합니다.
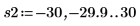
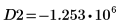
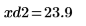
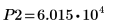
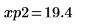
예상대로 그래프는 두 번째 최소값과 두 번째 최대값을 Y축 왼쪽에 보여줍니다.
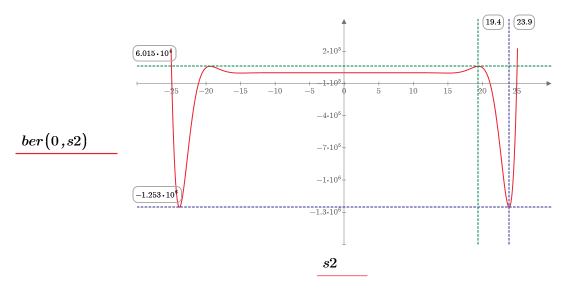
14. 마커를 사용하여 다음 번 최소값 (D3)과 다음 번 최대값 (P3)을 표시합니다.
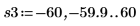
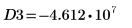
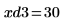
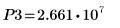
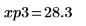
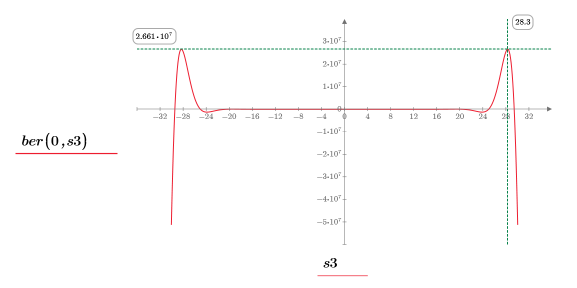
예상대로 그래프는 두 번째 최대값을 Y축 왼쪽에 보여줍니다.
최소값 (D3)과 그에 해당하는 좌변 값은 빈의 경계에 근접해 있으므로 무시하는 것이 좋습니다. |