예제: 역 변환 idft
벡터 작업(1D)
1. 벡터 v의 길이를 정의합니다.
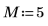
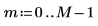
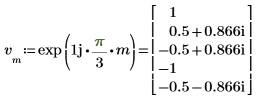
3. dft 함수를 사용하여 벡터 v의 정방향 변환을 계산합니다.
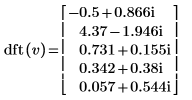
4. idft 함수를 사용하여 벡터 v의 역방향 변환을 계산합니다.

5. 벡터 v의 정방향 변환을 역방향 변환하면 원래 벡터 v임을 보여줍니다.
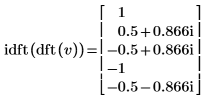 |  |
결과가 동일합니다.
행렬 작업(2D)
1. 행렬 C를 정의하고 계산합니다.
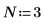
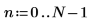
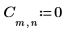
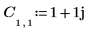
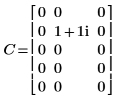
2. dft 함수를 사용하여 행렬 C의 정방향 변환을 계산합니다.

3. idft 함수를 사용하여 행렬 C의 역방향 변환을 계산합니다.

4. 행렬 C의 정방향 변환을 역방향 변환하면 원래 행렬 C임을 보여줍니다.
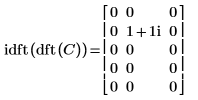 | 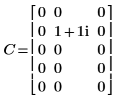 |
결과가 동일합니다.
idft의 기반이 되는 합계 설명
1차원의 경우:
1. exp 함수와 합계 연산자를 사용하여 벡터 v의 역방향 변환을 계산합니다.
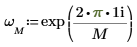
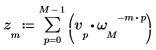
2. 결과로 얻은 벡터 v의 정방향 변환을 dft 함수의 출력과 비교합니다.
 | 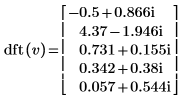 |
결과가 동일합니다.
3. 합계 연산자를 사용하여 벡터 v의 역방향 변환을 계산합니다.
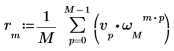
4. 결과로 얻은 벡터 v의 역방향 변환을 idft 함수의 출력과 비교합니다.
 |  |
결과가 동일합니다.
2차원의 경우:
1. exp 함수와 합계 연산자를 사용하여 행렬 C의 정방향 변환을 계산합니다.
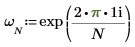
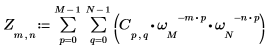
2. 결과로 얻은 행렬 C의 정방향 변환을 dft 함수의 출력과 비교합니다.


결과가 동일합니다.
3. 합계 연산자를 사용하여 행렬 C의 역방향 변환을 계산합니다.
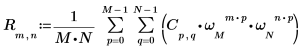
4. 결과로 얻은 행렬 C의 역방향 변환을 idft 함수의 출력과 비교합니다.


결과가 동일합니다.