예제: FFT의 소개
빠른 푸리에 변환(FFT)은 일정 시간에 걸쳐 측정된 데이터 집합의 주파수 콘텐츠를 나타내는 수치 해석 방법입니다. FFT에 사용되는 데이터는 파형을 형성하는 연속적인 데이터인 경우가 많습니다. 데이터를 수치로 해석하기 위해 일정한 시간 간격을 두고 특정 표본 비율로 샘플링합니다. 아래 그림은 샘플링된 파형과 주파수에 대해 도표화된 푸리에 변환의 강도를 보여 줍니다.
샘플링된 싸인파
1. sin 함수를 사용하여 싸인파를 정의합니다.
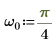
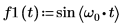
2. 데이터 점의 수를 설정합니다.
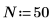
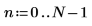
3. 표본 사이의 거리를 설정합니다.
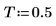
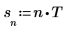
4. 표본 비율을 설정합니다.
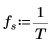
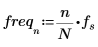
5. 싸인 함수를 도표화합니다.
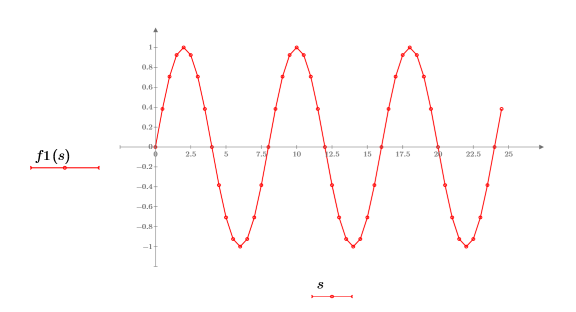
6. dft 함수를 사용하여 이산 푸리에 변환을 계산합니다.
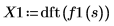
X1은 실수 및 복소수로 구성된 벡터입니다.
7. 최대 강도가 발생하는 주파수를 구합니다.
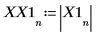
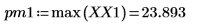
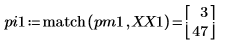
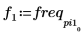
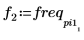
8. 변환된 신호를 도표화하고 마커를 사용하여 최대 강도의 크기와 주파수를 표시합니다.
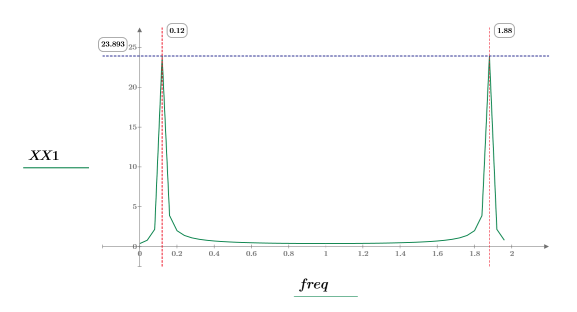
샘플링된 코사인파
1. cos 함수를 사용하여 코사인파를 정의합니다.
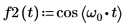
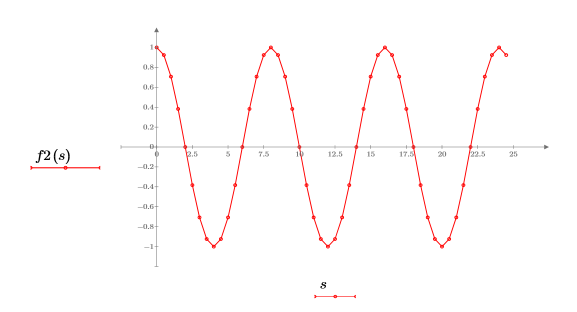
2. 코사인 함수를 도표화합니다.
3. dft 함수를 사용하여 이산 푸리에 변환을 계산합니다.
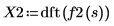
X2은 실수 및 복소수로 구성된 벡터입니다.
4. 최대 강도가 발생하는 시점의 주파수를 구합니다.
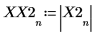
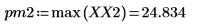
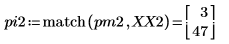
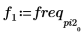
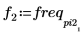
5. 변환된 신호를 도표화하고 마커를 사용하여 최대 강도의 크기와 주파수를 표시합니다.
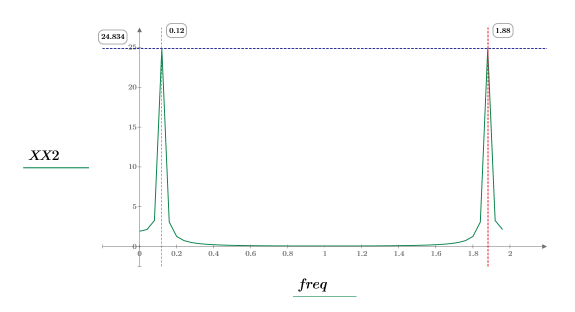
샘플링된 지수 파형
1. exp 함수를 사용하여 지수 파형을 정의합니다.
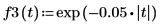
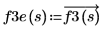
정의 내부의 행렬식 연산자는 단일 스칼라 값을 반환하기 때문에 함수의 요소 수준 값을 가져오기 위해 벡터화 연산자가 사용됩니다.
2. 지수 함수를 도표화합니다.
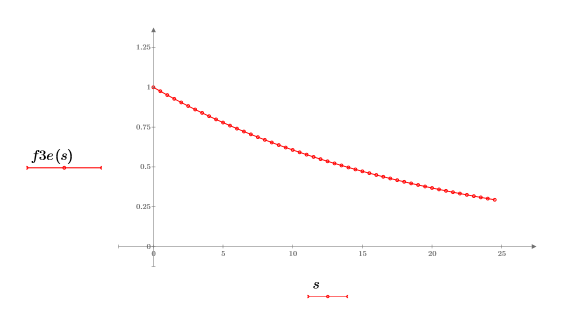
3. dft 함수를 사용하여 이산 푸리에 변환을 계산합니다.
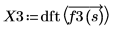
X3은 실수 및 복소수로 구성된 벡터입니다.
4. 최대 강도가 발생하는 시점의 주파수를 구합니다.
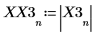
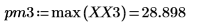
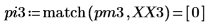
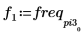
5. 변환된 신호를 도표화하고 마커를 사용하여 최대 강도의 크기와 주파수를 표시합니다.
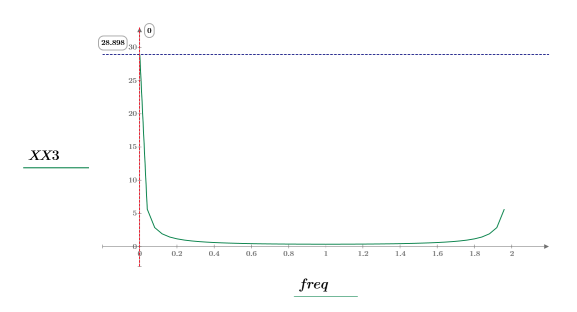
샘플링된 계단 파형
1. if 함수를 사용하여 계단파를 정의합니다.
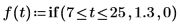
2. 각 구간의 충격 강도를 계산합니다.
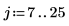
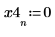
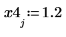
3. 계단 함수를 도표화합니다.
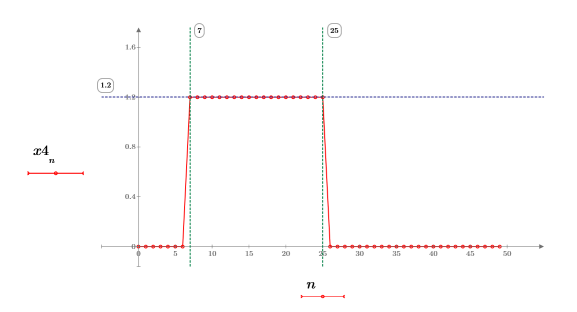
크기가 일정하고 7~25 사이에서 1.2와 같습니다.
4. dft 함수를 사용하여 이산 푸리에 변환을 계산합니다.
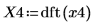
X4은 실수 및 복소수로 구성된 벡터입니다.
5. 최대 강도가 발생하는 시점의 주파수를 구합니다.
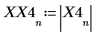
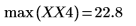
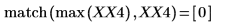
6. 변환된 신호를 도표화하고 마커를 사용하여 최대 강도의 크기와 주파수를 표시합니다.
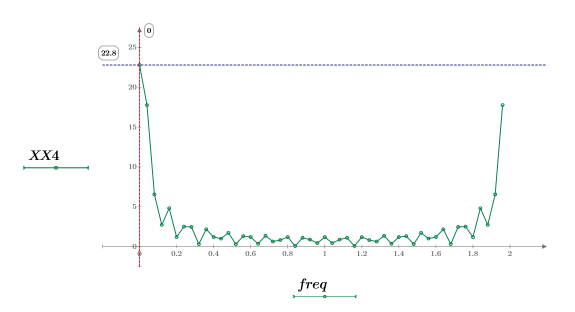
최대 강도는 freq0에서 발생합니다.