예제: 상호 작용
effects 함수를 사용하여 실험에서 상호 작용이 갖는 역할을 이해합니다.
1. fullfact 함수를 사용하여 인수가 두 개인 설계 행렬을 생성합니다.
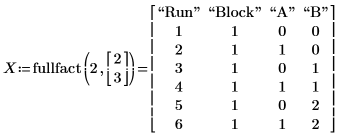
2. 행렬 Vals에 실험을 위한 실수 값을 지정합니다. 성별 인수를 남성(Male)과 여성(Female)을 나타내는 두 레벨로 분할합니다. 연령 인수를 청년(Young), 중년(Middle) 및 노년(Old)을 나타내는 세 레벨로 분할합니다. 인수별로 레벨 수가 같지 않으므로 Vals의 첫 행에 NaN를 삽입하여 빈(bin) 요소를 채웁니다.
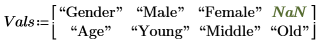
3. doelabel 함수를 사용하여 성별 및 연령에 따라 실험 결과를 정렬합니다.

행렬 X와 D가 가리키는 내용은 서로 동일하지만 X에는 인수의 코드화된 값이 표시되고 D에는 해당 실제 값이 표시된다는 점에서 차이가 있습니다.
상호 작용 없음 - 유효 인수가 한 개뿐인 경우
1. 각 그룹이 작업을 익히는 데 걸리는 평균 시간을 기록합니다. Run 1의 경우 젊은 남성의 평균 학습 시간이 9분입니다.
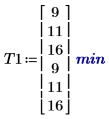
2. effects 함수를 호출하여 성별, 연령 및 이 둘의 상호 작용이 어떤 효과를 갖는지 확인합니다.

Gender 하위 행렬은 성별이 학습 시간에 영향을 미치지 않음을 보여줍니다. 따라서 보고 대상인 연령과 성별 사이에는 아무런 상호 작용 효과도 없습니다.
3. 연령이 학습 시간에 미치는 영향을 보여 주는 효과 도표를 만듭니다. 가장 젊은 그룹이 작업을 익히는 데 평균 9분이 소요됩니다.
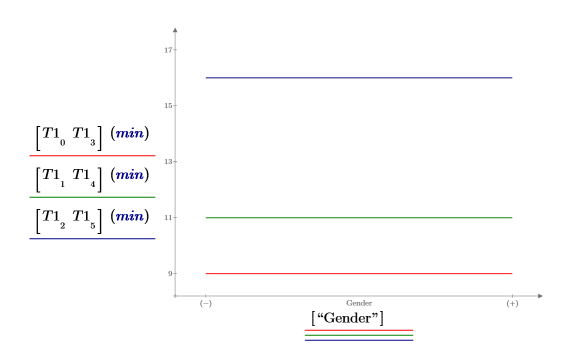
상호 작용 없음 - 유효 인수가 두 개인 경우
1. 각 그룹이 둘째 작업을 익히는 데 걸리는 평균 시간을 기록합니다.
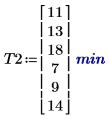
2. effects 함수를 호출하여 성별, 연령 및 이 둘의 상호 작용이 어떤 효과를 갖는지 확인합니다.

학습 과정에 연령이 미치는 영향은 첫째 작업의 경우와 같습니다. 그러나 이번에는 남성 피험자가 작업을 익히는 데 여성보다 더 많은 시간이 걸렸습니다.
3. A와 B의 각기 다른 레벨에서 AB의 상호 작용 효과를 계산하려면 i와 j를 A와 B의 레벨로 정의하고 mABi, j를 i와 j에서의 AB에 대한 평균 응답으로 정의합니다.

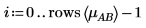
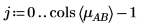
4. mean 함수를 사용하여 이 실험의 전체 평균과 각 인수의 평균을 계산합니다.
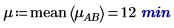
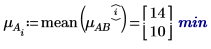
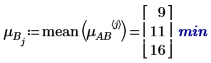
5. 각 인수에 대한 레벨 효과를 계산합니다.
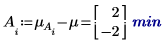
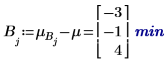
6. 인수 A와 B의 각 레벨에 대해 augment 함수를 사용하여 가산 인수 효과를 계산합니다. 이는 A 및 B의 각 레벨에 대해 전체 실험 평균, A의 레벨 효과 및 B의 레벨 효과를 모두 더한 값입니다.
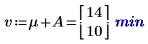
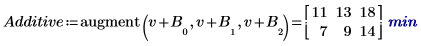
7. 상호 작용 효과를 계산합니다. 이는 AB에 대한 평균 응답과 A 및 B의 각 레벨에 대한 가산 인수 효과 사이의 차이입니다.
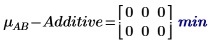
이 작업의 경우 연령과 성별 사이에는 아무런 상호 작용 효과도 없습니다.
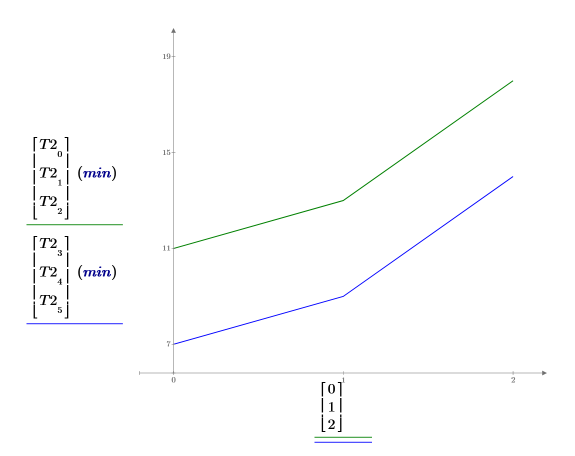
8. 각 성별의 평균 학습 시간을 도표화합니다. 젊은 여성이 둘째 작업을 익히는 데는 평균 7분이 소요됩니다. 성별과 연령 사이에 아무런 상호 작용 효과도 없으므로 두 곡선이 평행을 이룹니다.
중요한 상호 작용이 있는 경우
1. 각 그룹이 셋째 작업을 익히는 데 걸리는 평균 시간을 기록합니다. effects 함수를 호출하여 성별, 연령 및 이 둘의 상호 작용이 어떤 효과를 갖는지 확인합니다.
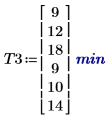

연령이 미치는 영향은 첫째 및 둘째 작업의 경우와 같지만 성별의 영향력은 둘째 작업의 경우보다 줄어들었습니다. 이 셋째 작업의 경우 연령과 성별 사이에 상호 작용 효과가 있습니다.
2. 상호 작용 효과를 계산합니다.

3. mean 함수를 사용하여 이 실험의 전체 평균과 각 인수의 평균을 계산합니다.
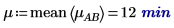
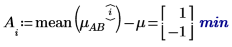
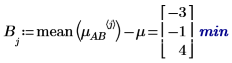
4. 인수 A와 B의 각 레벨에 대해 augment 함수를 사용하여 가산 인수 효과를 계산합니다. 이는 A 및 B의 각 레벨에 대해 전체 실험 평균, A의 레벨 효과 및 B의 레벨 효과를 모두 더한 값입니다.
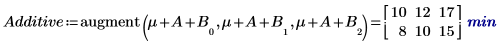
5. 상호 작용 효과를 계산합니다. 이는 AB에 대한 평균 응답과 A 및 B의 각 레벨에 대한 가산 인수 효과 사이의 차이입니다.
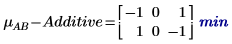
상호 작용 AB의 평균 응답과 가산 인수 효과 사이에 차이가 있습니다.
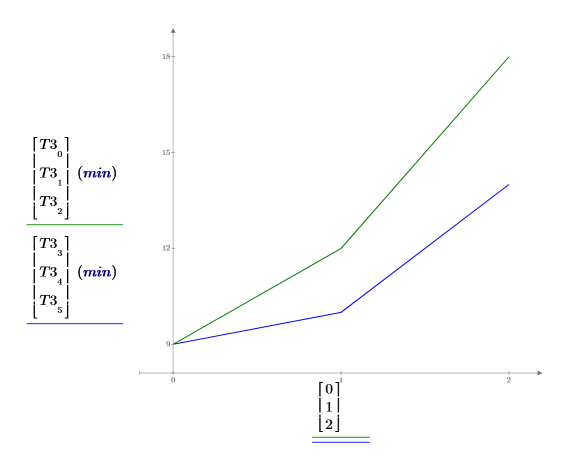
6. 각 성별의 평균 학습 시간을 도표화합니다. 청년층의 경우 남성과 여성의 학습 시간에 차이가 없지만 노년층의 경우 셋째 작업을 익히는 데 남성이 여성보다 더 많은 시간을 필요로 합니다. 연령와 성별 사이에 중요한 상호 작용이 있으므로 두 곡선이 평행을 이루지 않습니다.
중요하지 않은 상호 작용이 있는 경우
1. 각 그룹이 넷째 작업을 익히는 데 걸리는 평균 시간을 기록합니다.

2. effects 함수를 호출하여 성별, 연령 및 이 둘의 상호 작용이 어떤 효과를 갖는지 확인합니다.

성별과 연령이 미치는 영향은 셋째 작업의 경우와 매우 유사하게 나타납니다.
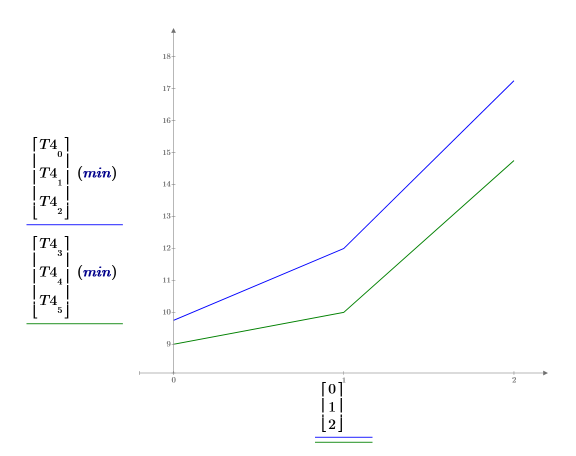
3. 각 성별의 평균 학습 시간을 도표화합니다. 두 곡선이 거의 평행을 이룹니다. 이는 연령과 성별 사이에 상호 작용이 있기는 하지만 그 상호 작용이 중요하지 않다는 의미입니다.
참조
J. Neter, M. H. Kutner, C. J. Nachtsheim, W. Wasserman, Applied Linear Statistical Models, 제4판, McGraw-Hill/Irwin, Boston, 1996년, 803.