예제: 영향력 있는 관측 확인
polyfitstat 함수를 사용하여 다변수 다항식 회귀를 생성하는 데 사용되는 관측을 검사합니다.
1. 25세에서 34세 사이의 신체 건강한 피험자 20명으로부터 수집한 표본을 포함하는 행렬을 정의합니다.
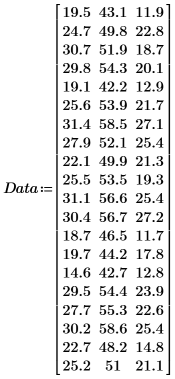
행렬의 열은 피험자 20명 각각의 삼두근 피하지방 두께, 넙다리 둘레 및 체지방률을 나타냅니다.
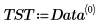
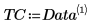
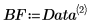
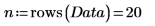
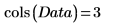
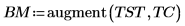
4. polyfitstat 함수를 호출하여 1차 회귀로 실험을 모델링하고 회귀 통계를 계산합니다.
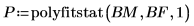
5. 출력 행렬 P의 행 7에서 구한 회귀 계수 행렬을 표시합니다.
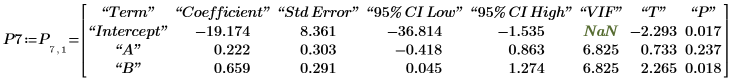
6. 행렬 계산을 사용하여 회귀 계수를 계산합니다.
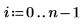
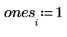
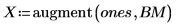
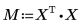
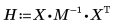
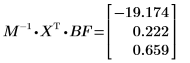
회귀 계수를 다음 방정식에 맞춥니다.
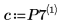
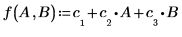
7. 회귀 방정식을 사용하여 체지방률의 예측값을 계산합니다. 이 값을 실제로 측정한 체지방률과 비교합니다.
 |  |
8. submatrix 함수를 사용하여 출력 행렬 P의 첫 행에서 구한 모델 통계를 표시합니다.

첫째 통계값은 회귀에 대한 표준 편차입니다.
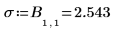
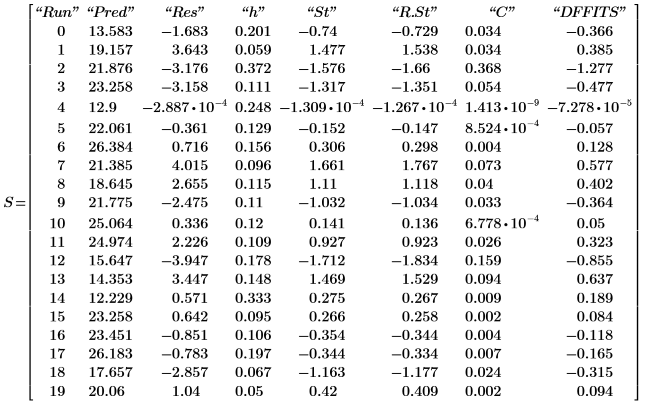
9. 출력 행렬 P의 마지막 중첩 행렬에서 구한 모델 진단값을 표시합니다.
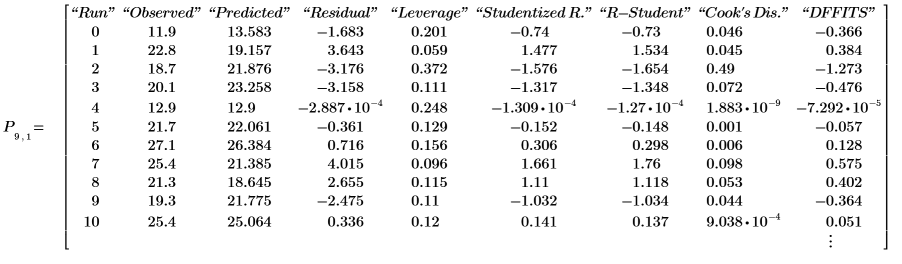
관측값과 예측값은 7단계에서 표시한 값에 상응합니다. 잉여값은 관측값과 예측값 사이의 차이입니다.
10. 잉여값, 즉 관측값과 예측값 사이의 차이를 계산합니다.
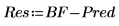
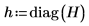
12. 스튜던트화된 잉여값을 계산합니다.
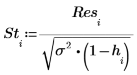
외부 스튜던트화된 잉여값, 즉 R 스튜던트 값은 다음과 같이 계산됩니다. 상수 p는 회귀에 대해 계산한 계수의 수이고, S2는 i번째 관측값이 제거된 데이터 집합을 기준으로 하는 s2의 추정치입니다.
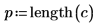
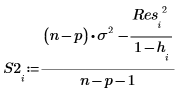
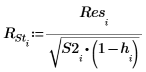
13. 쿡의 거리를 사용하여 삭제된 점이 선형 회귀에 미치는 전반적인 영향을 측정합니다.
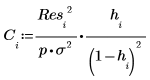
14. 모든 관측값을 적합식에 포함했을 때의 예측값과 i번째 관측값을 제외했을 때의 예측값 사이의 차이를 계산합니다.
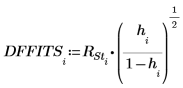
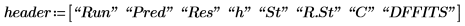
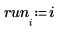
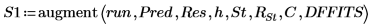
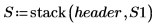
16. max 및 qt 함수를 사용하여 데이터 집합에서 최대 R 스튜던트 값을 구합니다. 본페로니(Bonferroni) 검사를 사용하여 해당 관측값이 이상치인지 여부를 확인합니다.
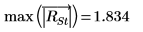
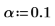
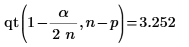
가장 큰 R 스튜던트 값이 본페로니 검사값보다 작습니다. 이는 해당 관측값이 이상치가 아니라는 의미입니다.
17. 최대 DFFITS 값을 구합니다.
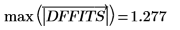
이 값이 1보다는 크지만 거의 1에 가까우므로 해당 관측값이 반드시 결과에 영향을 준다고는 단정할 수 없습니다.
18. 실험 실행(Run)별로 쿡의 거리를 도표화하여 지수 영향 도표를 만듭니다.
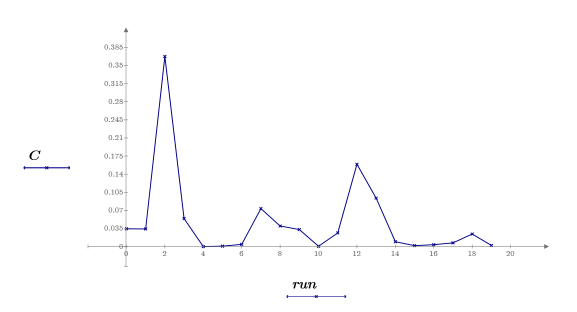
데이터 집합 중에서 run2에 대한 관측값이 가장 영향력이 높습니다. 10단계에서 확인한 run12에 대한 관측값도 영향력이 큰 편이지만 run2에 대한 관측값에 비하면 그 정도가 훨씬 덜합니다.
참조
참조: Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 제4판, McGraw-Hill/Irwin, Boston, 1996년, 페이지 375