예제: 정방향 변환 dft
dft 함수를 사용하여 표본 간의 시간이나 공간이 일정한 임의 크기의 실수 또는 복소 값 벡터나 행렬의 복소수 푸리에 변환을 구합니다.
1D 복소수 싸인 데이터
표본 간격 T의 N개 데이터 점으로 이루어진 시뮬레이션된 복소수 데이터 집합을 생성합니다.
1. 데이터 점 수를 정의합니다.
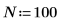
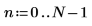
2. 표본을 수집할 시간 T를 정의합니다.
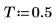
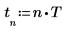
3. 각주파수를 설정합니다.
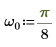
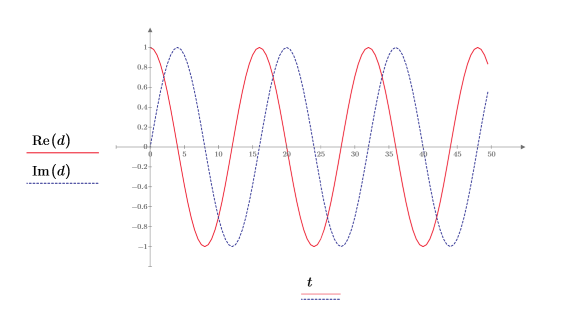
4. exp 함수를 사용하여 지수 함수를 정의합니다.
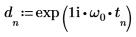
6. dft 함수를 적용하여 데이터를 주파수 영역으로 변환합니다.
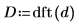
7. D의 절대값을 새 배열에 수집합니다.
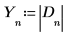
8. 변환된 벡터에서 n번째 항목에 대한 주파수와 표본 주파수를 정의합니다.
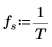
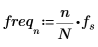
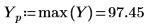
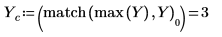
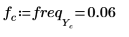
10. 변환된 벡터를 도표화하고 세로 및 가로 마커를 사용하여 진폭이 최대값이 되는 주파수를 표시합니다.
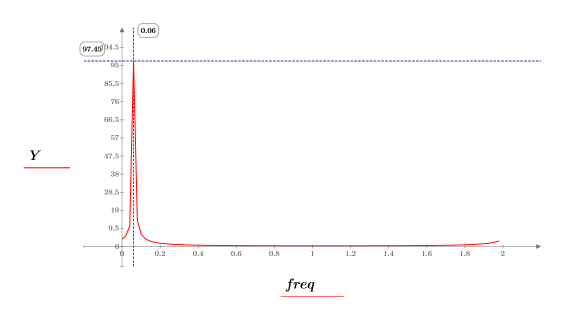
◦ 주파수 영역 표본의 앞쪽 절반은 음의 주파수를 나타냅니다.
◦ 이 복소수 신호에는 음의 주파수 콘텐츠가 없습니다.
추가 정보
• 실수 데이터 벡터 v에서 일반적으로 벡터 dft(v)는 복소수이며 중간 값을 중심으로 공액 대칭입니다. 실수 행렬의 경우 결과의 각 열이 공액 대칭입니다.
• 정방 배열 입력 A의 경우 dft(A)가 대칭입니다.
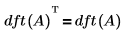
• 나이퀴스트 샘플링 이론에 따르면 샘플링 주파수가 푸리에 변환으로 해석하려는 가장 높은 주파수보다 2배 이상 높아야 합니다.
• 데이터 점의 수가 큰 소수 값인 경우 빠른 푸리에 변환에 사용되는 소인수 알고리즘의 속도가 저하됩니다. 이러한 문제는 잘 발생하지 않지만 매우 큰 소인수의 데이터 점을 사용하는 경우 이 점을 주의해야 합니다.