예제: 데이터 평활
movavg, expsmooth 및 medsmooth 함수를 사용하여 이동 평균, 지수 데이터 평균 또는 중앙값 필터링을 수행합니다. 이들 함수는 데이터 집합에 포함된 각 점과 그 이웃한 점 사이의 평균을 구하여 데이터의 불규칙성을 줄이는 방식으로 데이터를 평활합니다.
이동 평균
횟수를 나타내는 t = 0, 1, 2, . . . , n - 2에 대해 t에서 평활화된 값은 t회를 포함하여 해당 회수까지 관측한 모든 수치에 대한 산술 평균입니다. n번의 관측을 수행했을 때 t회에 평활화된 값은 t회의 관측값과 이전 n - 1번의 관측값에 대한 평균입니다.
1. sin 함수를 사용하여 감쇄하는 싸인 신호를 정의합니다.
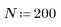
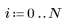
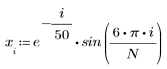
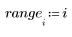
2. 신호에 노이즈를 추가하기 위해 rnd 함수를 사용하여 크기는 일정하지만 무작위한 컴포넌트를 적용합니다.
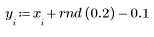
3. movavg 함수를 호출하고 너비가 각각 2, 10 및 20인 창을 사용하여 데이터를 평활합니다.

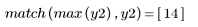
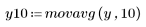
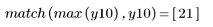
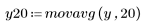
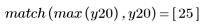
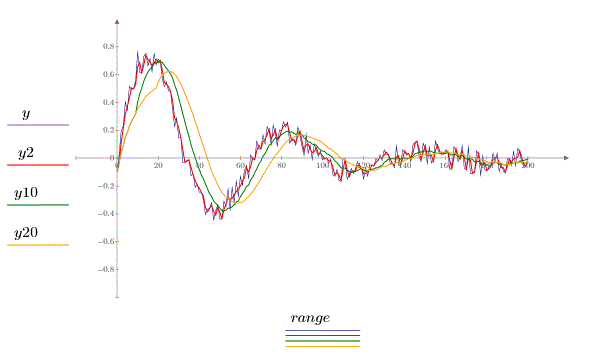
창 너비가 크면 시차가 발생합니다.
지수 평균
계단 함수를 사용하여 movavg 및 expsmooth 사이의 차이를 확인합니다. 지수 데이터 평균은 다음과 같이 계산됩니다.
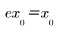
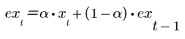
여기서 t = 1, . . . , last(x) 입니다.
t회에 평활화한 성분은 현재 관측값과 이전에 평활화한 관측값에 대해 가중치 α를 사용하여 구한 평균입니다.
1. 계단 함수를 정의하고 도표화합니다.
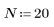 | 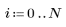 |
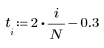 | t가 음수일 때 함수를 0으로 설정하기 위해 0.3을 더했습니다. |
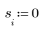 | |
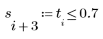 | 너비가 1.0인 펄스를 얻기 위해 1 대신 0.7을 사용했습니다. |
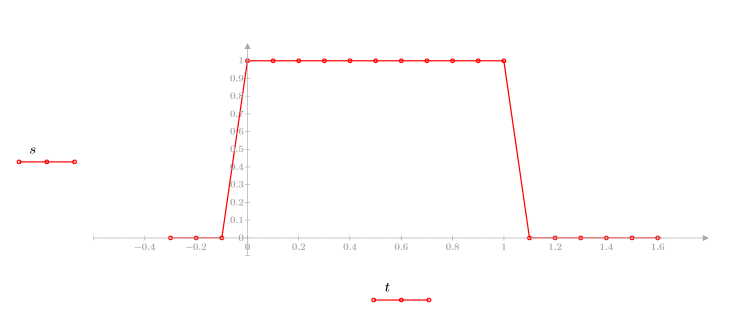
2. 너비가 4인 창을 사용하여 계단 함수에 movavg 함수를 적용합니다.
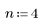
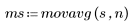
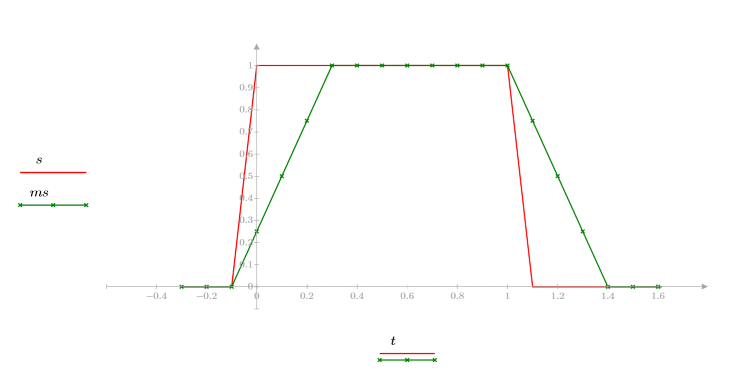
계단 함수에 movavg 함수를 적용하면 n=4를 표본으로 하여 1-to-0 사이에서 매끄러운 변환이 이루어집니다.
3. 가중치로 0.5를 사용하여 계단 함수에 expsmooth 함수를 적용합니다.
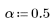
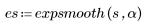
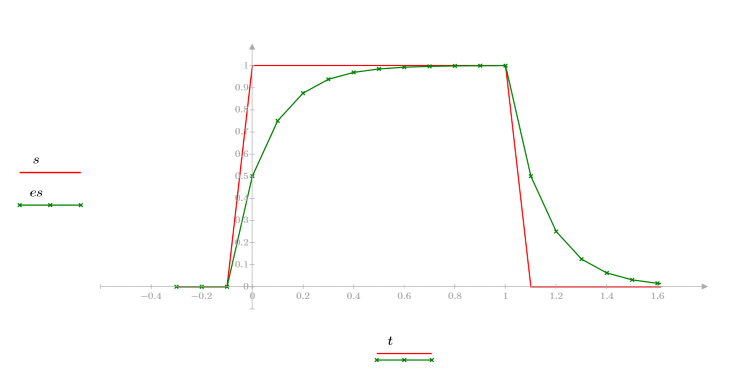
계단 함수에 expsmooth 함수를 적용하면 표본 10개를 사용하여 1-to-0 사이에서 매끄러운 곡선으로 변환이 이루어집니다.
시장 추세를 예측하기 위해 movavg와 같은 방식으로 expsmooth를 사용할 수도 있지만 실무에 있어서 대부분의 전문가들은 동일한 기초형상 데이터에 대해 가중치를 다르게 적용하여 구한 두 가지 지수 평활 사이의 차이 같은 다른 지표를 사용합니다.
중앙값 필터링
중앙값 필터링에서는 입력 정보의 각 요소를 해당 요소와 신호의 끝 지점 근처에 있는 n-1개 이하의 이웃 요소에 대한 중앙값으로 바꿉니다. 이 방법은 윤곽선을 유지하면서 노이즈를 줄여 평활하려는 경우에 적합합니다.
행렬이 큰 경우에는 각 픽셀에서 정렬을 수행해야 하기 때문에 이 함수를 실행하는 데 시간이 오래 걸릴 수 있습니다. 중앙값 필터링 방법을 사용하면 노이즈를 제거할 수 있을 뿐만 아니라 예리하고 짧은 과도 신호도 상당 부분 제거할 수 있습니다.
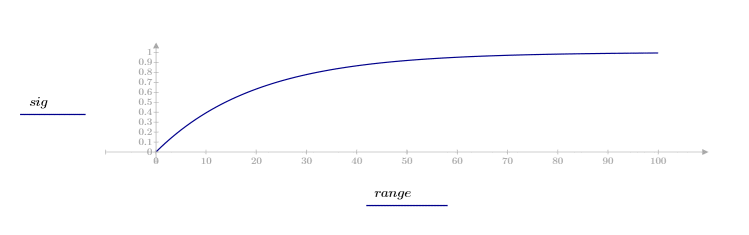
1. 지수 신호를 정의하고 도표화합니다.
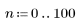
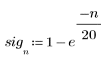
2. whiten 함수를 사용하여 난수 백색 노이즈를 추가해 신호 품질을 저하시킵니다.
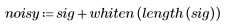
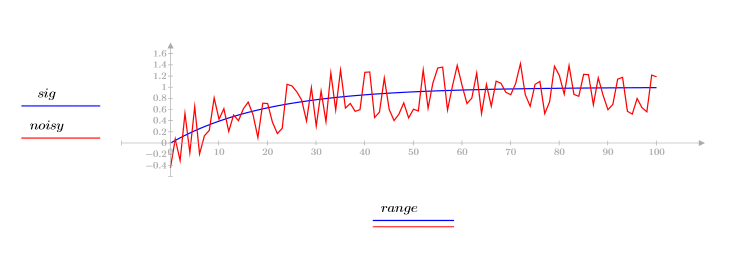
3. medsmooth 함수를 사용하여 중앙값 필터를 적용한 다음 필터링된 신호를 도표화합니다.
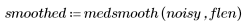
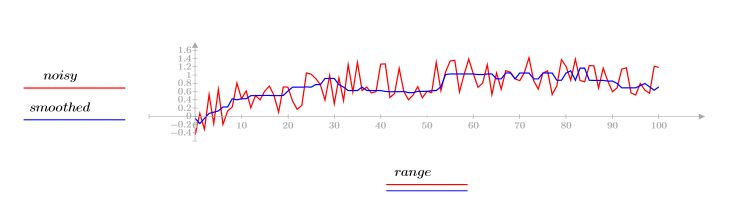
신호를 필터링하여 좀 더 매끄러운 결과를 얻었습니다.
필터의 길이를 바꿨을 때 노이즈 신호에 어떤 영향을 주는지 살펴봅니다. 실무에서는 중앙값 필터의 길이가 신호의 길이보다 짧아야 합니다.