예제: 켑스트럼 및 복소 켑스트럼
켑스트럼은 컨볼루션과 디컨볼루션을 주파수 영역에서 더하기와 빼기로 매핑하며, 음성 신호 가공과 지구 물리 신호 가공 분야에 사용됩니다.
cepstrum
시퀀스 x(n)의 켑스트럼은 다음과 같은 수식으로 계산됩니다.
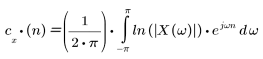
여기서 X(ω)는 시퀀스 x(n)의 푸리에 변환입니다.
이것은 x(n)의 푸리에 변환에 자연 로그를 적용한 후 역 변환하는 정의입니다. 로그는 시간 영역의 컨볼루션을 주파수 영역의 더하기로 매핑하므로 빼기로 매핑되는 신호 디컨볼루션에서 켑스트럼을 유용하게 사용할 수 있습니다.
1. n의 범위를 정의합니다.
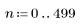
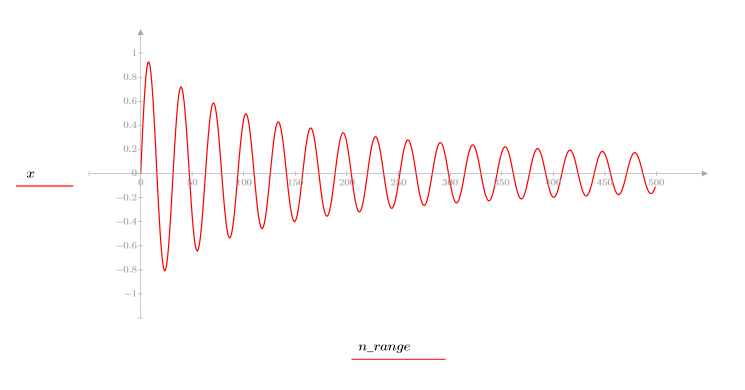
2. 시퀀스 함수 x를 정의합니다.
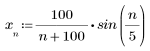
3. 시퀀스 함수 x를 도표화합니다.
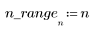
4. 켑스트럼을 계산하고 결과 함수를 도표화합니다.
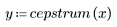
5. recenter 함수를 사용하여 첫 번째 요소가 가운데에 오도록 결과의 중심을 조정합니다.
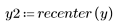
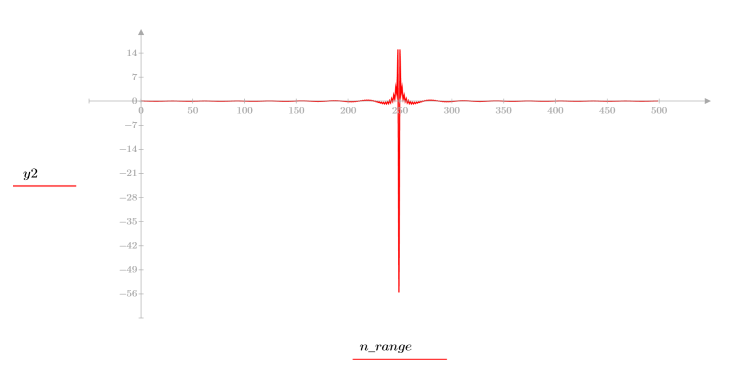
켑스트럼에서는 위상 정보가 유지되지 않으므로 원래 신호를 복구할 수 없습니다.
ccepstrum
복소 켑스트럼 함수는 다음과 같은 복소수 알고리즘으로 계산됩니다.
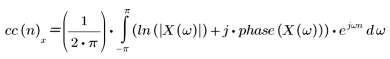
여기서 X(ω)는 시퀀스 x(n)의 푸리에 변환이고 phase는 지정된 시퀀스의 위상 정보를 표현하는 데 사용됩니다.
출력 신호의 ccepstrum을 입력 및 채널 시퀀스의 ccepstrum과 비교하면 출력의 ccepstrum이 입력 및 채널의 ccepstrum 합계라는 것을 알 수 있습니다. 이것은 주파수 영역에서 두 신호의 스펙트럼을 더하는 것과 유사하지만 시간 영역에서 수행한다는 것이 다릅니다.
다음 예제에서는 에코를 발생시키는 통신 채널을 이동하는 신호를 시뮬레이션합니다(Oppenheim and Schaefer의 12.8.1절, Prentice-Hall, 1989년).
1. 채널 응답을 다른 시퀀스의 감쇄 복사 신호(에코)를 발생시키는 FIR 필터로 정의하고 도표화합니다.
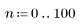
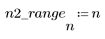
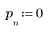
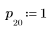
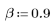
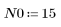
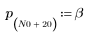
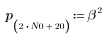
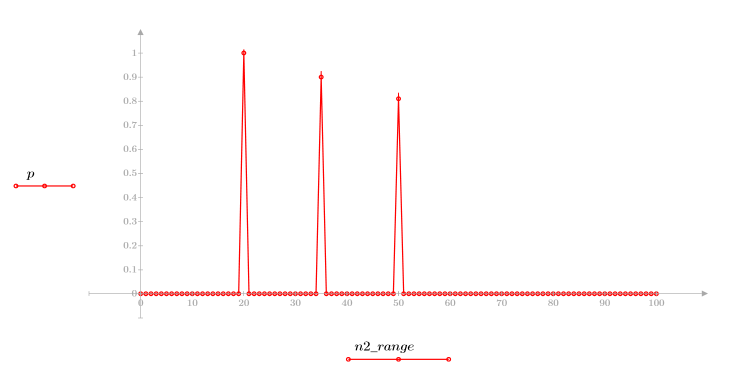
2. 채널 응답과 컨볼루션될 시퀀스 v를 정의하고 도표화합니다.
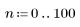
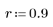
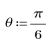
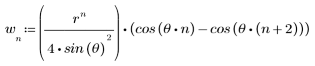
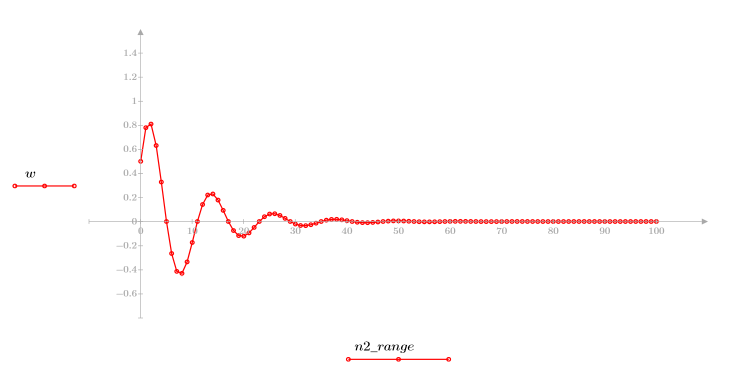
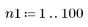
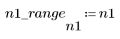
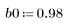
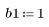
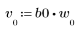
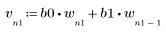
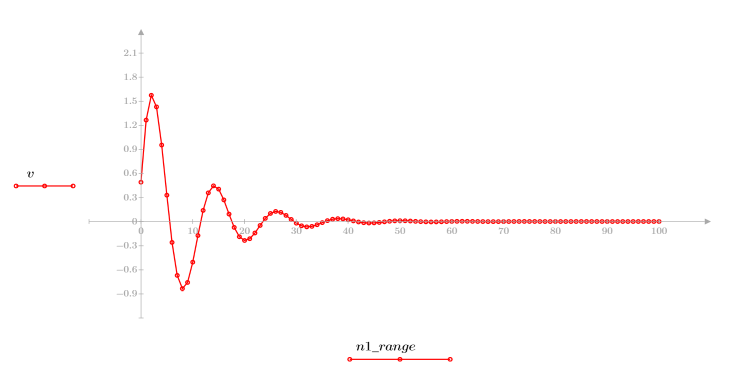
3. response 함수를 사용하여 계수 배열 v(통신 채널 함수 v)의 FIR 필터에 대한 입력 벡터 p의 n항 벡터 응답을 얻습니다.
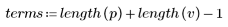
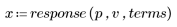
4. 응답 함수를 도표화합니다.
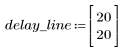
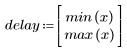
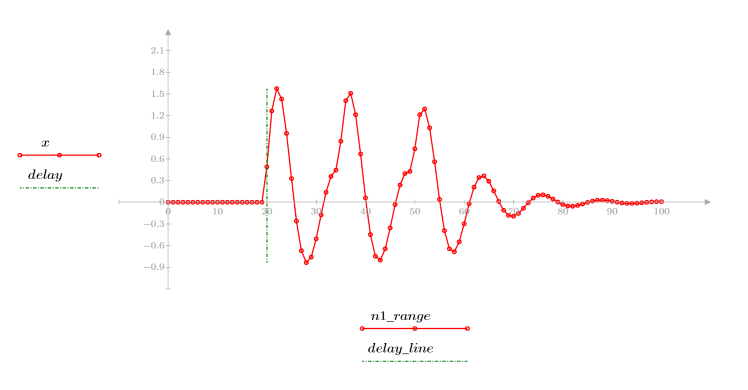
◦ 결과 시퀀스는 입력 함수 p 및 통신 채널 함수 v의 컨볼루션입니다.
◦ 이 시퀀스는 원래 신호에 지연된 복제 신호를 더하여 보여 줍니다.
5. 출력 신호의 복소 켑스트럼을 원래 시퀀스의 켑스트럼과 비교합니다. 비교가 쉽도록 결과의 중심을 조정합니다.
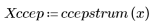
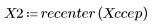
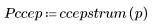
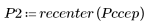
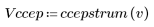
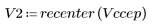
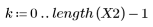
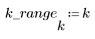
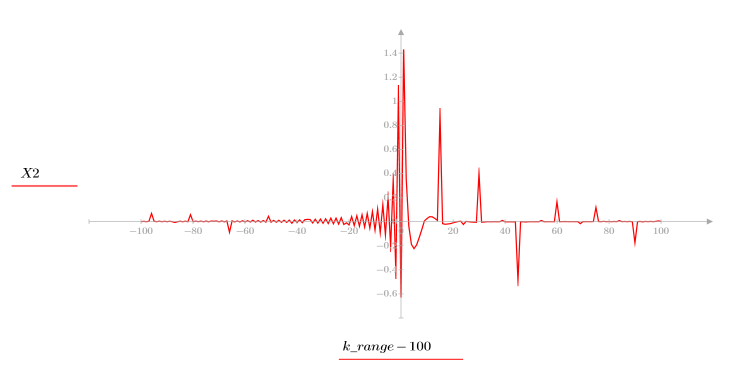
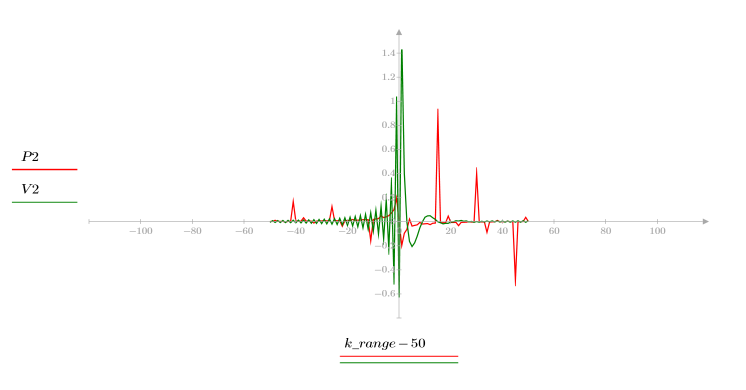
위 도표에서 출력 신호의 복소 켑스트럼이 서로 컨볼루션된 두 시퀀스의 복소 켑스트럼 합계임을 알 수 있습니다.