예제: 코쉬 분포

함수 > 통계 > 확률 분포 > 예제: 코쉬 분포

예제: 코쉬 분포

1. 코쉬 분포의 정의를 표시합니다.

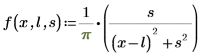
여기서

◦ l은 위치 매개변수(평균)입니다.

◦ s는 배율 매개변수(분산의 제곱근)이며 s > 0입니다.

2. 위치 및 배율 매개변수 집합 세 개를 정의한 다음 위치 및 배율 매개변수 l0 및 s0에서 곡선의 진폭(또는 높이)을 계산합니다.

<region id="ID0E5JQBB" top="307.20000000000005" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="239"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> </math> </region>	<region id="ID0ETKQBB" top="307.20000000000005" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="241"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> </math> </region>	<region id="ID0EILQBB" top="307.20000000000005" left="211.20000000000005" height="27.791200000000003" width="53.826666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="243"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>-2</real> </define> </math> </region>
<region id="ID0EAMQBB" top="268.80000000000007" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="233"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> </math> </region>	<region id="ID0EUMQBB" top="268.80000000000007" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="235"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>1</real> </define> </math> </region>	<region id="ID0EINQBB" top="268.80000000000007" left="211.20000000000005" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="237"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>1</real> </define> </math> </region>

<region id="ID0E1NQBB" top="364.80000000000007" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="245">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

3. dcauchy 함수를 사용하여 서로 다른 값의 위치 매개변수와 고정 배율 매개변수에서 값 x에 대한 확률 밀도를 구합니다.

<region id="ID0E3PQBB" top="460.80000000000007" left="38.400000000000006" height="307.19999999999993" width="556.4000000000002" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="247">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="248">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="DashDot">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="249">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="360.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="250">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="251">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="252" display="true" color="#FFED1D2F" line-style="Dash" value="0.31830988618379069">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="254">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="255">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="256">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="257">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="258">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="259">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

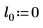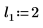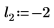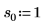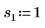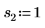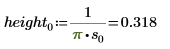
서로 다른 위치 매개변수 값은 X축 방향으로 곡선을 이동합니다.

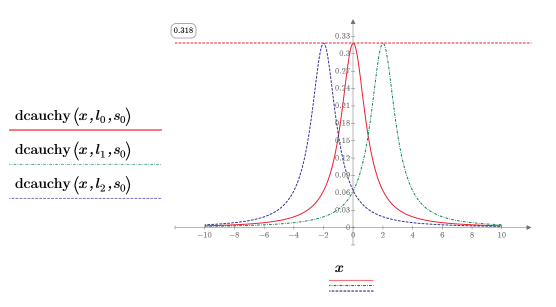
4. 고정된 위치 매개변수와 서로 다른 배율 매개변수 값을 사용하여 dcauchy 함수를 도표화합니다.

<region id="ID0E3SQBB" top="940.80000000000018" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="275"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ERTQBB" top="940.80000000000018" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="277"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EGUQBB" top="940.80000000000018" left="192.00000000000003" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="279"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0E5UQBB" top="902.40000000000009" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="269"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ESVQBB" top="902.40000000000009" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="271"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EGWQBB" top="902.40000000000009" left="192.00000000000003" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="273"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>3</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

<region id="ID0EYWQBB" top="998.40000000000009" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="281">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EGXQBB" top="1036.8000000000002" left="38.400000000000006" height="307.2" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="283">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="284">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="285">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="286">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="287">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="288" display="true" color="#FF068149" line-style="Dash" value="0.15915494309189535">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="290">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="291">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="292">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="293">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="294">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="295">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

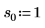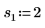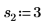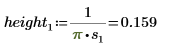
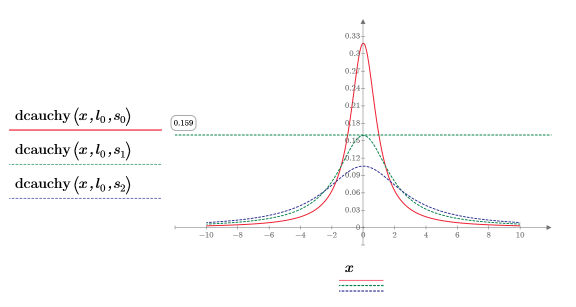
서로 다른 배율 매개변수 값은 곡선의 높이를 변경합니다.

5. 서로 다른 위치 매개변수와 배율 매개변수 값을 사용하여 dcauchy 함수를 도표화합니다.

<region id="ID0EG1QBB" top="1497.6000000000001" left="38.400000000000006" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="311"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>0</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E21QBB" top="1497.6000000000001" left="115.20000000000002" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="313"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EQ2QBB" top="1497.6000000000001" left="192.00000000000003" height="27.791200000000003" width="43.076666666666668" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="315"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>4</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EI3QBB" top="1459.2000000000003" left="38.400000000000006" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="305"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span> </id> <real>1</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E33QBB" top="1459.2000000000003" left="115.20000000000002" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="307"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span> </id> <real>2</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EQ4QBB" top="1459.2000000000003" left="192.00000000000003" height="27.791200000000003" width="44.806666666666672" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="309"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span> </id> <real>3</real> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

<region id="ID0EC5QBB" top="1555.2000000000003" left="38.400000000000006" height="49.391200000000005" width="170.46666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="317">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <eval>
 <apply>
 <div />
 <real>1</real>
 <apply>
 <mult />
 <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

<region id="ID0EQ5QBB" top="1747.2000000000003" left="38.400000000000006" height="307.2" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="319">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="320">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="321">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="322">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="323">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.33">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>12</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="324" display="true" color="#FF2E3192" line-style="Dash" value="0.1061032953945969">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
 height<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="326">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="327">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="328">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="329">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="330">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">dcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id labels="VARIABLE" xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="331">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

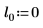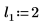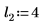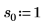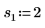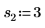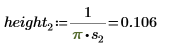
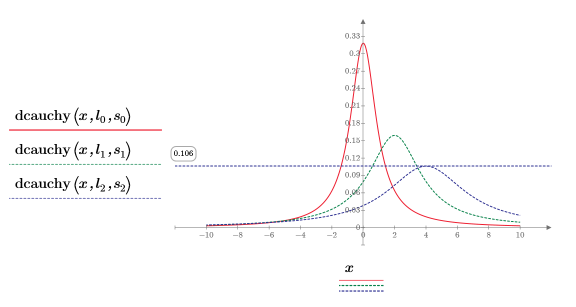
서로 다른 배율 및 위치 매개변수는 곡선을 이동하고 곡선의 높이를 변경합니다.

6. 서로 다른 값의 위치 매개변수와 고정 배율 매개변수를 사용하여 pcauchy 함수를 도표화합니다.

<region id="ID0ETARBB" top="2169.6000000000004" left="38.400000000000006" height="326.4" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="341">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="342">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="343">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="344">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="345">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker display="true" color="#FF000000" line-style="Dash" value="1" />
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="352">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="353">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="354">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="355">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="356">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="357">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="347">
 <real xmlns="http://schemas.mathsoft.com/math50">0.0</real>
 </startValue>
 <secondTickValue resultRef="349">
 <real xmlns="http://schemas.mathsoft.com/math50">0.2</real>
 </secondTickValue>
 <endValue resultRef="351">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

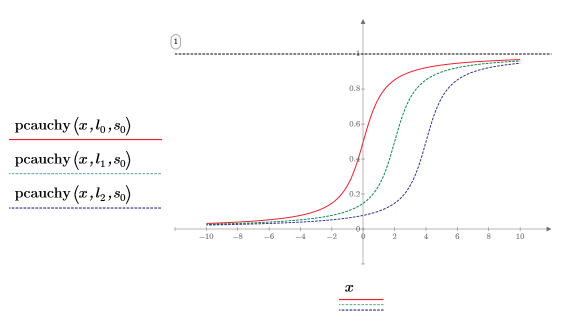
◦ 서로 다른 위치 매개변수 값은 X축 방향으로 곡선을 이동합니다.

◦ pcauchy의 모든 y 값은 0과 1 사이에 있습니다.

7. 고정된 위치 매개변수와 서로 다른 배율 매개변수 값을 사용하여 pcauchy 함수를 도표화합니다.

<region id="ID0ESFRBB" top="2668.8" left="38.400000000000006" height="326.4" width="575.6" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="373">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="374">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="375">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="379.6" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-10" end="10">
 <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="376">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="377">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="378" display="true" color="#FF000000" line-style="Dash" value="0.5">
 <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
 </marker>
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="386">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="387">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="388">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="389">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="390">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">pcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="391">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="381">
 <real xmlns="http://schemas.mathsoft.com/math50">0.0</real>
 </startValue>
 <secondTickValue resultRef="383">
 <real xmlns="http://schemas.mathsoft.com/math50">0.2</real>
 </secondTickValue>
 <endValue resultRef="385">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

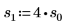
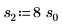
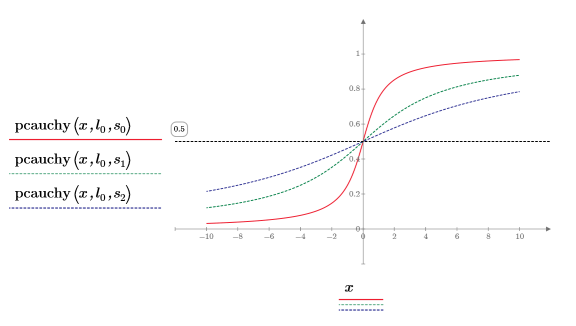
◦ 서로 다른 배율 매개변수 값은 곡선을 수평 방향으로 평평하게 만들지만 모든 곡선은 y=0.5에서 교차합니다.

◦ pcauchy의 모든 y 값은 0과 1 사이에 있습니다.

8. 서로 다른 값의 위치 매개변수와 고정 배율 매개변수를 사용하여 qcauchy 함수를 도표화합니다.

<region id="ID0EEKRBB" top="3110.4000000000005" left="38.400000000000006" height="326.4" width="576.4" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace num-of-points="500" resultRef="404">
 <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="405">
 <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 <trace num-of-points="500" resultRef="406">
 <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="380.4" height="249.6" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="1">
 <axisLine position="origin" positionticmark="3" legendWidth="60.93" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker display="true" color="#FF000000" line-style="Dash" value="1" />
 </markers>
 <plotEquations>
 <plotEquation>
 <math resultRef="411">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
 </math>
 <math resultRef="412">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="408">
 <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
 </startValue>
 <endValue resultRef="410">
 <real xmlns="http://schemas.mathsoft.com/math50">1</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-15" end="15">
 <axisLine position="origin" positionticmark="5" legendWidth="170.26" />
 <axisGrid>
 <gridFrequency>7</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="419">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="420">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="421">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="422">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="423">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="FUNCTION" xml:space="preserve">qcauchy</id>
 <sequence>
 <id xml:space="preserve">x</id>
 <id xml:space="preserve">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript>
 </id>
 <id xml:space="preserve">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </math>
 <math resultRef="424">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="414">
 <real xmlns="http://schemas.mathsoft.com/math50">-15</real>
 </startValue>
 <secondTickValue resultRef="416">
 <real xmlns="http://schemas.mathsoft.com/math50">-10</real>
 </secondTickValue>
 <endValue resultRef="418">
 <real xmlns="http://schemas.mathsoft.com/math50">15</real>
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

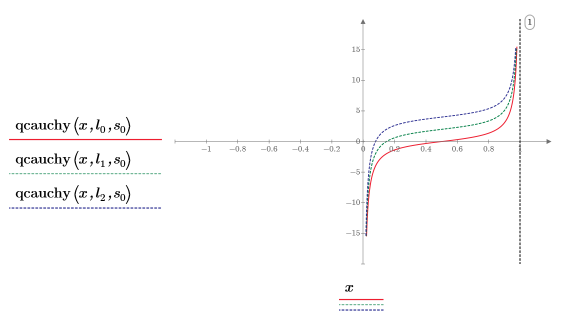
◦ 서로 다른 위치 매개변수 값은 Y축 방향으로 곡선을 이동합니다.

◦ qcauchy의 모든 x 값은 0과 1 사이에 있습니다.

9. 고정 위치 및 배율 매개변수를 사용하여 rcauchy 함수를 계산합니다.

<region id="ID0EKPRBB" top="3648.0000000000005" left="38.400000000000006" height="27.791200000000003" width="169.31666666666666" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="442">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">R</id>
 <parens>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rcauchy</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 l<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 s<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </parens>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="true" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

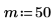
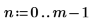
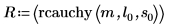
함수 rcauchy는 코쉬 분포에 따라 난수 m개의 벡터를 구합니다.

10. rcauchy 함수로 구한 난수를 도표화합니다.

<region id="ID0EKRRBB" top="3744.0000000000005" left="38.400000000000006" height="288" width="576.39999999999986" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="444">
 <traceStyle color="#FFED1D2F" symbol="filledStar" line-weight="2" line-style="None">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="476.4" height="230.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="50">
 <axisLine position="origin" positionticmark="6" legendWidth="61.7533333333333" />
 <axisGrid>
 <gridFrequency>6</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="451">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">n</id>
 </math>
 <math resultRef="452">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="446">
 <real xmlns="http://schemas.mathsoft.com/math50">0</real>
 </startValue>
 <secondTickValue resultRef="448">
 <real xmlns="http://schemas.mathsoft.com/math50">10</real>
 </secondTickValue>
 <endValue resultRef="450">
 <real xmlns="http://schemas.mathsoft.com/math50">50</real>
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-12" end="8">
 <axisLine position="origin" positionticmark="0" legendWidth="69.59" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <plotEquations>
 <plotEquation>
 <math resultRef="453">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <indexer />
 <id xml:space="preserve">R</id>
 <id xml:space="preserve">n</id>
 </apply>
 </math>
 <math resultRef="454">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

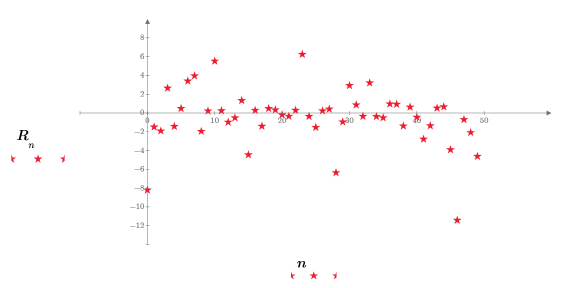
워크시트를 다시 계산하면 rcauchy 함수가 새 난수 집합을 구하고, 그에 따라 도표가 업데이트됩니다.