예제: 풀이 구간에 단위 추가

풀이 구간 > 예제: 풀이 구간에 단위 추가

예제: 풀이 구간에 단위 추가

풀이 구간에 단위를 추가할 수 있습니다. 계산 전체에서 단위가 서로 호환되는지 확인해야 합니다.

1. 진자의 길이를 정의합니다.

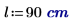
2. 풀이 구간을 삽입하고 문제에 대한 미분 방정식을 정의한 다음 odesolve 함수를 사용하여 방정식을 풉니다. 각도 Ɵ는 수직과 진자 사이의 각도입니다.

<region id="ID0EP21JB" actualWidth="233" actualHeight="221.39999999999998" top="230.40000000000003" left="38.400000000000006" height="221.39999999999998" width="233" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="174.87333333333333" actualHeight="56.369333557128911" top="43.2" left="24" solve-block-category="constraint">
 <math resultRef="92">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <derivative />
 <lambda>
 <boundVars>
 <id xml:space="preserve">t</id>
 </boundVars>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </lambda>
 <degree>
 <real>2</real>
 </degree>
 </apply>
 <apply>
 <mult />
 <apply>
 <neg />
 <apply>
 <div />
 <id labels="UNIT" xml:space="preserve">g</id>
 <id xml:space="preserve">l</id>
 </apply>
 </apply>
 <apply>
 <id xml:space="preserve">sin</id>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="61.693333333333342" actualHeight="25.6" top="96" left="24" solve-block-category="constraint">
 <math resultRef="94">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <id xml:space="preserve">θ</id>
 <real>0</real>
 </apply>
 <real>0</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="64.786666666666676" actualHeight="25.6" top="144" left="24" solve-block-category="constraint">
 <math resultRef="96">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <apply>
 <functionDerivative />
 <id xml:space="preserve">θ</id>
 </apply>
 <real>0</real>
 </apply>
 <real>2</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="164.43666666666667" actualHeight="25.6" top="196.8" left="24" solve-block-category="solver">
 <math resultRef="98">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Θ</id>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">odesolve</id>
 <sequence>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 <real>10</real>
 </sequence>
 </apply>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

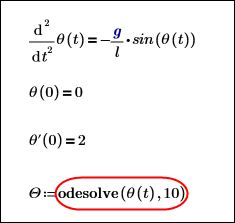
길이 l과 중력 상수 g 모두 단위가 있습니다.

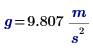
하지만 초기 조건과 끝점에는 단위가 없습니다. 결과적으로 단위 호환성 관련 오류가 나타납니다.

3. 모든 풀이 구간 컴포넌트에 호환되는 단위를 추가합니다.

<region id="ID0E541JB" actualWidth="233" actualHeight="223" top="614.40000000000009" left="38.400000000000006" height="223" width="233" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="174.87333333333333" actualHeight="56.369333557128911" top="43.2" left="24" solve-block-category="constraint">
 <math resultRef="102">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <derivative />
 <lambda>
 <boundVars>
 <id xml:space="preserve">t</id>
 </boundVars>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </lambda>
 <degree>
 <real>2</real>
 </degree>
 </apply>
 <apply>
 <mult />
 <apply>
 <neg />
 <apply>
 <div />
 <id labels="UNIT" xml:space="preserve">g</id>
 <id xml:space="preserve">l</id>
 </apply>
 </apply>
 <apply>
 <id xml:space="preserve">sin</id>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="73.346666666666678" actualHeight="25.6" top="96" left="24" solve-block-category="constraint">
 <math resultRef="104">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <id xml:space="preserve">θ</id>
 <apply>
 <scale />
 <real>0</real>
 <id xml:space="preserve">s</id>
 </apply>
 </apply>
 <real>0</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="104.56" actualHeight="29.752000000000002" top="144" left="24" solve-block-category="constraint">
 <math resultRef="106">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <apply>
 <functionDerivative />
 <id xml:space="preserve">θ</id>
 </apply>
 <apply>
 <scale />
 <real>0</real>
 <id xml:space="preserve">s</id>
 </apply>
 </apply>
 <apply>
 <mult />
 <real>2</real>
 <apply>
 <pow />
 <id xml:space="preserve">s</id>
 <real>-1</real>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="176.67666666666668" actualHeight="25.6" top="196.8" left="24" solve-block-category="solver">
 <math resultRef="108">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Θ</id>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">odesolve</id>
 <sequence>
 <apply>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 <apply>
 <scale />
 <real>10</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

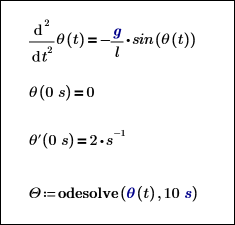
4. 풀이 구간 해를 도표화할 값 범위를 정의합니다. 단위가 있는 범위를 정의할 때에는 단계 범위 연산자를 사용해야 합니다.

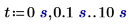
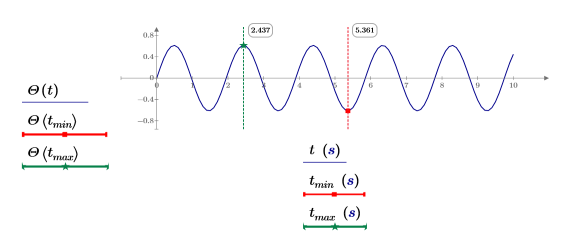
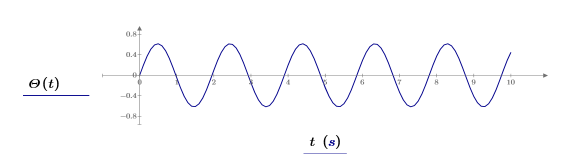
5. 풀이 구간 해를 도표화합니다.

<region id="ID0E5A2JB" actualWidth="576" actualHeight="168.00000000000003" top="998.40000000000009" left="38.400000000000006" height="168.00000000000003" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="112">
 <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="460.8" height="110.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
 <axisLine position="origin" positionticmark="2" legendWidth="60.71" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="113">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
 </math>
 <math resultRef="114">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.8" end="0.8">
 <axisLine position="origin" positionticmark="0" legendWidth="84.5333333333333" />
 <axisGrid>
 <gridFrequency>5</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="119">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </apply>
 </math>
 <math resultRef="120">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="116">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.8</real>
 </startValue>
 <secondTickValue resultRef="118">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.4</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

6. 풀이 구간을 구성한 다음 minimize 함수를 사용하여 주어진 추측값 t=5 s에서 Ɵ가 최소값이 되는 때를 구합니다.

<region id="ID0EBD2JB" actualWidth="300" actualHeight="100" top="1209.6000000000001" left="38.400000000000006" height="100" width="300" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="50.683333333333337" actualHeight="25.6" top="38.400000000000006" left="19.200000000000003" solve-block-category="guess-value">
 <math resultRef="127">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>5</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </define>
 </math>
 </region>
 <region id="" actualWidth="218.85999999999999" actualHeight="27.791200000000003" top="76.800000000000082" left="19.200000000000003" solve-block-category="solver">
 <math resultRef="129">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="*" xml:space="preserve">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 <eval>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">minimize</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

추측값의 단위는 최소화할 함수의 정의와 호환되어야 합니다.

7. 풀이 구간을 구성한 다음 maximize 함수를 사용하여 주어진 추측값 t=2 s 및 제약 조건 t<4 s에서 Ɵ가 최대값이 되는 때를 구합니다.

<region id="ID0EMF2JB" actualWidth="311.96333333333337" actualHeight="135" top="1440.0000000000002" left="38.400000000000006" height="135" width="311.96333333333337" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="50.683333333333337" actualHeight="25.6" top="38.400000000000006" left="19.200000000000003" solve-block-category="guess-value">
 <math resultRef="131">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>2</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 <region id="" actualWidth="48.513333333333335" actualHeight="25.6" top="76.800000000000011" left="19.200000000000003" solve-block-category="constraint">
 <math resultRef="133">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <lessThan />
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>4</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </apply>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 <region id="" actualWidth="223.94666666666669" actualHeight="27.791200000000003" top="115.20000000000002" left="19.200000000000003" solve-block-category="solver">
 <math resultRef="135">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="*" xml:space="preserve">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 <eval>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">maximize</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

8. SIUnitsOf 함수를 사용하여 최대 및 최소 점에서 단위를 제거합니다. 단위 없는 세로 마커를 사용하려면 이 작업이 필요합니다.

<region id="ID0EKH2JB" actualWidth="230.05666666666667" actualHeight="51.582400000000007" top="1689.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="137">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">max</id>
 <eval>
 <apply>
 <div />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">SIUnitsOf</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

<region id="ID0EYH2JB" actualWidth="226.24666666666664" actualHeight="51.582400000000007" top="1766.4000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="139">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">min</id>
 <eval>
 <apply>
 <div />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">SIUnitsOf</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

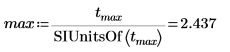
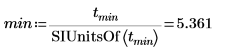
9. 원래 도표에 최대 점과 최소 점을 표시합니다. 세로 마커를 사용하여 이 두 점이 시간 축과 교차하는 위치를 표시합니다.

<region id="ID0EIJ2JB" actualWidth="577.2" actualHeight="244.80000000000004" top="1881.6000000000004" left="38.400000000000006" height="244.80000000000004" width="577.2" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="141">
 <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="142">
 <traceStyle color="#FFFF0000" symbol="filledRectangle" line-weight="2" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="143">
 <traceStyle color="#FF068149" symbol="filledStar" line-weight="2" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="442.8" height="110.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
 <axisLine position="origin" positionticmark="2" legendWidth="81.8666666666667" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="144" display="true" color="#FF068149" line-style="Dash" value="2.4368823377188966">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">max</id>
 </marker>
 <marker resultRef="146" display="true" color="#FFED1D2F" line-style="Dash" value="5.3611508941582011">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </marker>
 </markers>
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="148">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
 </math>
 <math resultRef="149">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="150">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </math>
 <math resultRef="151">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="152">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </math>
 <math resultRef="153">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.8" end="0.8">
 <axisLine position="origin" positionticmark="0" legendWidth="105.763333333333" />
 <axisGrid>
 <gridFrequency>5</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="158">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </apply>
 </math>
 <math resultRef="159">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="160">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </apply>
 </math>
 <math resultRef="161">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="162">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </apply>
 </math>
 <math resultRef="163">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="155">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.8</real>
 </startValue>
 <secondTickValue resultRef="157">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.4</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>