ODE ソルバ
• 次の各関数は (intvls+1)×(n+1) の解行列を返します (ここで、n は未知数の数)。行列の最初の列には、解が評価された点の x の値が含まれています。これらの値は x1 から x2 の間を (intvls + 1) 個に等間隔で区切った点の数値です。以降の列には、最初の列の x の値に対応する解 y0,y1,...,yn-1 の値が含まれています。
• rkfixed、RkAdapt、Bulstoer、Stiffb、Stiffr の各ソルバでは、ソルバを呼び出す前に変数 TOL を定義することで、解にスカラーの許容誤差を指定できます。たとえば、すべての変数の許容誤差を 10-6 に設定できます。
TOL:=10-6
TOL はソルバ Adams、BDF、Radau には影響しません。これらのソルバで許容誤差を指定するには、オプションの引数 tol を使用する必要があります。
• ODE ソルブブロックを使用すると、方程式および初期条件の入力を簡素化できます。
スティフでない連立方程式のソルバ
• Adams(init, x1, x2, intvls, D, [tol]) - Adams 法を使用します。
• rkfixed(init, x1, x2, intvls, D) - 固定増分による 4 次のルンゲ-クッタ法を使用します。
• Rkadapt(init, x1, x2, intvls, D) - 適応増分による 4 次のルンゲ-クッタ法を使用します。
• Bulstoer(init, x1, x2, intvls, D) - Bulirsch-Stoer 法を使用します。これはルンゲ-クッタ法より正確ですが、常微分方程式の変化が穏やかである必要があります。
スティフな連立方程式のソルバ
スティフな ODE 問題や代数 ODE 問題を解く場合に使用します。
• BDF(init, x1, x2, intvls, D, [J], [tol]) - 後退差分公式法を使用します。オプションの引数 J または tol のどちらかを使用できます。
• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) - Radau5 法を使用します。オプションの引数 J、M、tol のうち、必要なものを自由に組み合わせて使用できます。
• Stiffb(init, x1, x2, intvls, D, AJ) - Bulirsch-Stoer 法を使用します。
• Stiffr(init, x1, x2, intvls, D, AJ) - Rosenbrock 法を使用します。
ハイブリッドソルバ
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) - 解がスティフかどうかを調べ、結果に応じて Adams または BDF を呼び出します。オプションの引数 J または tol のどちらかを使用できます。
引数
• init は、n 個の実数による初期値のベクトル (ここで n は未知数の数)、または 1 つの常微分方程式の場合は 1 つのスカラーの初期値です。
• x1 と x2 は、常微分方程式の解を求める区間の始点と終点を表す実数のスカラーです。初期値 init は、x1 で評価された常微分方程式関数の値です。
• intvls は、解の関数を補間するときに使用する離散化間隔の数を示す整数です。間隔の数に 1 を加えた数が解の点の数になります。
• D は、方程式の右辺を指定する D(x,y) という形式のベクトル関数です。
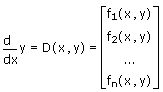
• tol (オプション) は、方程式の各独立変数の許容誤差を指定する実数値または実数値のベクトルです。許容誤差は解の変数に必要な精度です。
◦ tol は 10-5 以下に設定します。問題の大きさと相対ステップサイズに基づいて、TOL の値を減らして、適切な解を求める必要があります。tol の値を小さくすると、必要な精度を確保するためにソルバのアルゴリズムが実行するステップが増えます。
◦ 連立方程式を解く場合、tol をスカラーに設定すると、連立方程式内のすべての変数に同じ許容誤差が設定されます。tol を連立方程式内の変数の数と等しい長さのベクトルに設定すると、変数ごとに許容誤差が指定されます。
• J (オプション) は、ヤコビ行列 (D で表される連立方程式の y0,y1,...yn-1 についての偏微分係数行列) を返す J(x, y) という形式の関数です。
• M (オプション) は、M · dy/dt = f(t, y) という形式の変数間のカップリングを表す実行列です。
• AJ は拡大ヤコビ行列を返す AJ(x, y) という形式の関数です。拡大ヤコビ行列の最初の列には、連立方程式の右辺の x についての偏導関数が含まれています。残りの列は、y0,y1,...yn-1 についての偏微分を含むヤコビアン J の列になります。
D、J、AJ の各関数は引数なしでソルバに渡され、関数 yn(x) は引数なしで D、J、AJ に指定されます。
D、J、AJ の 2 番目の引数は、成分が 1 つだけの場合でもベクトルとして添字を付ける必要があります。
追加情報
• 関数 Radau と Rkadapt は、微分方程式を解くときに内部で等区間でないステップを使用し、解の変化が大きい領域ではステップ数を増やします。ただし、intvls に指定されている等間隔の点の数における解を返します。
• Radau 関数は、シンボリックなヤコビ行列を入力する必要がないので便利です。ただし、J が実際にある場合は、J を使うと精度が向上します。