Invariants de moment

Fonctions > Traitement d'image > Extraction de caractéristiques > Invariants de moment

Invariants de moment

• moment_invariant(M) : renvoie un vecteur contenant les sept invariants de moment typiques de M.

Les invariants de moment (définis par Hu en 1962) sont des combinaisons de moments spatiaux normalisés jusqu'au troisième degré. Ils ne sont pas modifiés par la translation, la rotation ni la mise à l'échelle de l'image. Les invariants de moments sont très utiles pour les problèmes d'identification de motifs, tels que la reconnaissance optique des caractères (OCR).

Les invariants de moments sont définis de la manière suivante :

Cliquez pour copier cette expression

<region id="ID0E2JHZ" top="76.800000000000011" left="76.800000000000011" height="71.75200000000001" width="101.22666666666666" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="5">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <indexer />
        <id xml:space="preserve">n</id>
        <sequence>
          <id xml:space="preserve">p</id>
          <id xml:space="preserve">q</id>
        </sequence>
      </apply>
      <apply>
        <div />
        <apply>
          <indexer />
          <id xml:space="preserve">μ</id>
          <sequence>
            <id xml:space="preserve">p</id>
            <id xml:space="preserve">q</id>
          </sequence>
        </apply>
        <apply>
          <pow />
          <parens>
            <apply>
              <indexer />
              <id xml:space="preserve">μ</id>
              <sequence>
                <real>0</real>
                <real>0</real>
              </sequence>
            </apply>
          </parens>
          <id xml:space="preserve">γ</id>
        </apply>
      </apply>
    </apply>
  </math>
</region>

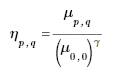
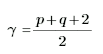
où p et q sont les degrés du moment normalisé dans les directions horizontale et verticale, et μp, q est le moment spatial central de degré (p, q).

Le moment central est défini comme :

<region id="ID0EWLHZ" top="211.20000000000005" left="76.800000000000011" height="50.000000000000007" width="295.58000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="9">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <indexer />
        <id xml:space="preserve">γ</id>
        <sequence>
          <id xml:space="preserve">p</id>
          <id xml:space="preserve">q</id>
        </sequence>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">i</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">j</id>
              </boundVars>
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <apply>
                      <pow />
                      <parens>
                        <apply>
                          <minus />
                          <id xml:space="preserve">j</id>
                          <apply>
                            <indexer />
                            <id xml:space="preserve">c</id>
                            <id xml:space="preserve">j</id>
                          </apply>
                        </apply>
                      </parens>
                      <id xml:space="preserve">p</id>
                    </apply>
                    <apply>
                      <pow />
                      <parens>
                        <apply>
                          <minus />
                          <id xml:space="preserve">i</id>
                          <apply>
                            <indexer />
                            <id xml:space="preserve">c</id>
                            <id xml:space="preserve">i</id>
                          </apply>
                        </apply>
                      </parens>
                      <id xml:space="preserve">q</id>
                    </apply>
                  </apply>
                  <apply>
                    <indexer />
                    <id xml:space="preserve">M</id>
                    <sequence>
                      <id xml:space="preserve">i</id>
                      <id xml:space="preserve">j</id>
                    </sequence>
                  </apply>
                </apply>
              </parens>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id xml:space="preserve">ncol</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id xml:space="preserve">nrow</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </apply>
  </math>
</region>

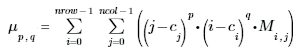
où nrow et ncol sont le nombre de lignes et colonnes de l'image d'entrée M, et (cj, ci) est le centre de gravité de l'image.

Arguments

• M est une matrice d'images.

Rubriques associées

A propos des fonctions d'extraction de caractéristiques

Exemple : Invariants de moment

Est-ce que cela a été utile ?