Aplatissement et asymétrie

Fonctions > Statistiques > Statistiques descriptives > Aplatissement et asymétrie

• kurt(A, B, C, ...) : renvoie l'aplatissement des éléments A, B, C, .... L'aplatissement est défini de la manière suivante :

<region id="ID0EGW46" top="96.000000000000014" left="0" height="67.041333333333341" width="609.23666666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="3">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <minus />
      <parens>
        <apply>
          <mult />
          <apply>
            <div />
            <apply>
              <mult />
              <apply>
                <mult />
                <id xml:space="preserve">m</id>
                <id xml:space="preserve">n</id>
              </apply>
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <id xml:space="preserve">m</id>
                    <id xml:space="preserve">n</id>
                  </apply>
                  <real>1</real>
                </apply>
              </parens>
            </apply>
            <apply>
              <mult />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <id xml:space="preserve">m</id>
                      <id xml:space="preserve">n</id>
                    </apply>
                    <real>1</real>
                  </apply>
                </parens>
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <id xml:space="preserve">m</id>
                      <id xml:space="preserve">n</id>
                    </apply>
                    <real>2</real>
                  </apply>
                </parens>
              </apply>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id xml:space="preserve">m</id>
                    <id xml:space="preserve">n</id>
                  </apply>
                  <real>3</real>
                </apply>
              </parens>
            </apply>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">i</id>
              </boundVars>
              <apply>
                <summation />
                <lambda>
                  <boundVars>
                    <id xml:space="preserve">j</id>
                  </boundVars>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <div />
                        <apply>
                          <minus />
                          <apply>
                            <indexer />
                            <id xml:space="preserve">M</id>
                            <sequence>
                              <id xml:space="preserve">i</id>
                              <id xml:space="preserve">j</id>
                            </sequence>
                          </apply>
                          <apply>
                            <id xml:space="preserve">mean</id>
                            <id xml:space="preserve">M</id>
                          </apply>
                        </apply>
                        <apply>
                          <id xml:space="preserve">Stdev</id>
                          <id xml:space="preserve">M</id>
                        </apply>
                      </apply>
                    </parens>
                    <real>4</real>
                  </apply>
                </lambda>
                <lowerBound>
                  <real>0</real>
                </lowerBound>
                <upperBound>
                  <apply>
                    <minus />
                    <id xml:space="preserve">n</id>
                    <real>1</real>
                  </apply>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id xml:space="preserve">m</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </apply>
      </parens>
      <apply>
        <div />
        <apply>
          <scale />
          <real>3</real>
          <apply>
            <pow />
            <parens>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <id xml:space="preserve">m</id>
                  <id xml:space="preserve">n</id>
                </apply>
                <real>1</real>
              </apply>
            </parens>
            <real>2</real>
          </apply>
        </apply>
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <mult />
                <id xml:space="preserve">m</id>
                <id xml:space="preserve">n</id>
              </apply>
              <real>2</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <mult />
                <id xml:space="preserve">m</id>
                <id xml:space="preserve">n</id>
              </apply>
              <real>3</real>
            </apply>
          </parens>
        </apply>
      </apply>
    </apply>
  </math>
</region>

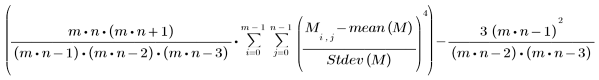
L'aplatissement d'un ensemble de valeurs indique à quel point la distribution est plate ou présente des pics par rapport à la loi normale :

Valeur	Forme de distribution
kurt = 0	Loi normale
kurt > 0	Distribution présentant des pics relatifs
kurt < 0	Distribution relativement plate

• skew(A, B, C, ...) : renvoie l'asymétrie des éléments A, B, C, .... L'asymétrie est définie de la manière suivante :

<region id="ID0ER346" top="192.00000000000003" left="19.200000000000003" height="67.041333333333341" width="355.64666666666676" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="5">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <scale />
      <apply>
        <div />
        <apply>
          <mult />
          <id xml:space="preserve">m</id>
          <id xml:space="preserve">n</id>
        </apply>
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <mult />
                <id xml:space="preserve">m</id>
                <id xml:space="preserve">n</id>
              </apply>
              <real>1</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <mult />
                <id xml:space="preserve">m</id>
                <id xml:space="preserve">n</id>
              </apply>
              <real>2</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">i</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">j</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <div />
                    <apply>
                      <minus />
                      <apply>
                        <indexer />
                        <id xml:space="preserve">M</id>
                        <sequence>
                          <id xml:space="preserve">i</id>
                          <id xml:space="preserve">j</id>
                        </sequence>
                      </apply>
                      <apply>
                        <id xml:space="preserve">mean</id>
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                    <apply>
                      <id xml:space="preserve">Stdev</id>
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>3</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id xml:space="preserve">m</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </apply>
  </math>
</region>

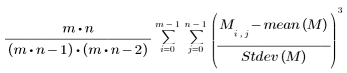
L'asymétrie d'un ensemble de valeurs est mesurée par rapport à la moyenne :

Valeur	Forme de distribution
skew = 0	La distribution est symétrique autour de sa moyenne, comme c'est le cas de la distribution normale.
skew > 0	La "queue" de la distribution s'étend vers des valeurs positives.
skew < 0	La "queue" de la distribution s'étend vers des valeurs négatives.

Arguments

• A, B, C, ... sont des scalaires ou tableaux. Il doit y avoir au moins quatre éléments dans les arguments de la fonction kurt, et au moins trois pour skew.

• M est un tableau créé à partir des arguments de fonctions A, B, C, .... L'écart-type de M ne doit pas être égal à zéro.

Rubriques associées

A propos des fonctions statistiques descriptives

Loi normale

Fonctions de moyenne

Exemple : Aplatissement et asymétrie

Est-ce que cela a été utile ?