Sinus et cosinus intégrales

Fonctions > Fonctions symboliques > Sinus et cosinus intégrales

• Si(x) : l'intégrale de la fonction sinus est définie comme suit :

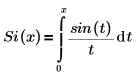
La représentation du développement en série est :

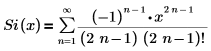
Le résultat affiché représente, trois des six termes par défaut de la série qui n'ont pas de coefficients de 0.

<region id="ID0E3N5BB" actualWidth="187.70000000000002" actualHeight="52.158666666666669" top="192.00000000000003" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Si</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <minus />
            <id xml:space="preserve" labels="*">x</id>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>3</real>
              </apply>
              <real>18</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>5</real>
            </apply>
            <real>600</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

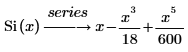
• Ci(x) : l'intégrale de la fonction cosinus est définie comme suit :

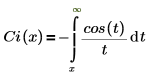
Une autre forme de la définition est :

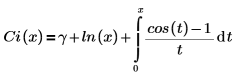
La représentation du développement en série est :

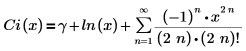
Les deux derniers termes représentent deux des six termes par défaut de la série qui n'ont pas de coefficients de 0.

<region id="ID0EJR5BB" actualWidth="234.19000000000003" actualHeight="52.158666666666669" top="460.80000000000007" left="364.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="38">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Ci</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <minus />
            <apply>
              <plus />
              <id xml:space="preserve" labels="CONSTANT">γ</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ln</id>
                <id xml:space="preserve" labels="*">x</id>
              </apply>
            </apply>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>2</real>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>4</real>
            </apply>
            <real>96</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

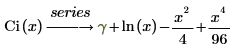
• Shi(x) : l'intégrale de la fonction sinus hyperbolique est définie comme suit :

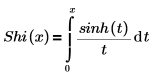
Le résultat affiché représente, trois des six termes par défaut de la série qui n'ont pas de coefficients de 0.

<region id="ID0EQT5BB" actualWidth="196.13333333333335" actualHeight="52.158666666666669" top="595.2" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="42">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">[Shi]</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <plus />
            <id xml:space="preserve" labels="*">x</id>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>3</real>
              </apply>
              <real>18</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>5</real>
            </apply>
            <real>600</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

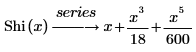
Les termes du développement en série des fonctions Si et Shi sont identiques, à l'exception du signe des termes lorsque n est pair.

• Chi(x) : l'intégrale de la fonction cosinus hyperbolique est définie comme suit :

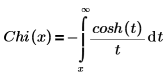
Une autre forme de la définition est :

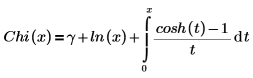
Les deux derniers termes représentent deux des six termes par défaut de la série qui n'ont pas de coefficients de 0.

<region id="ID0E2W5BB" actualWidth="242.62333333333336" actualHeight="52.158666666666669" top="806.40000000000009" left="364.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">[Chi]</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <plus />
            <apply>
              <plus />
              <id xml:space="preserve" labels="CONSTANT">γ</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ln</id>
                <id xml:space="preserve" labels="*">x</id>
              </apply>
            </apply>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>2</real>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>4</real>
            </apply>
            <real>96</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

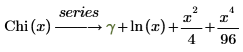
Les termes du développement en série des fonctions Ci et Chi sont identiques, à l'exception du signe des termes lorsque n est impair.

Arguments

• x est un scalaire réel ou complexe, ou un vecteur de scalaires réels ou complexes.

Informations supplémentaires

Ces fonctions sont utiles lorsque vous utilisez le mot-clé float, qui évalue numériquement les fonctions au lieu de retourner des mathématiques symboliques.

Rubriques associées

A propos des fonctions symboliques

Exemple : Utilisation de fonctions symboliques intégrales sinus et cosinus

Pour développer une expression d'une série de Taylor ou de Laurent

Est-ce que cela a été utile ?