Fonctions gamma
• Γ(z) : renvoie la valeur de la fonction eulérienne gamma en z.
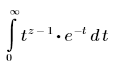
Voici des relations portant sur la fonction gamma, qui peuvent être utiles :
◦ Γ(z + 1) = z · Γ(z)
◦ Γ(z)·Γ(1 − z) = π · csc(π · z)
◦ Γ(n + 1) = n!
• Γ(a, x) : renvoie la valeur de la fonction gamma incomplète en x avec le paramètre a. Γ(a, 0) = Γ(a).
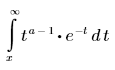
• lnΓ(z) : renvoie le logarithme népérien de valeur en z de la fonction eulérienne gamma.
Pour saisir Γ, appuyez sur G,Ctrl+G.
Utilisez la fonction lnΓ pour renvoyer des résultats inférieurs, puis les mettre à l'échelle.
• Psi(y): renvoie la dérivée du logarithme népérien de la fonction Γ(y).
Arguments
• z est un scalaire réel, ou complexe, sans dimension, indéfini pour z = 0, −1, −2...
Pour Γ(z), seuls les arguments −107 ≤ Re(z) ≤ 171 et −106 ≤ Im(z) ≤ 106 peuvent être évalués sans dépassement numérique. Pour z complexe, Γ(z) est le prolongement analytique de la fonction réelle.
• a est un scalaire réel positif, sans dimension.
• x est un scalaire réel positif, sans dimension ou le nombre 0.
• y est un nombre réel.