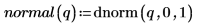Exemple : Score Z d'un vecteur de données

Fonctions > Statistiques > Lois de probabilité > Exemple : Score Z d'un vecteur de données

Calcul d'un score Z pour un vecteur de données normalement distribuées par rapport à un écart-type défini de la population.

1. Définissez un jeu de données à analyser.

2. Calculez la moyenne de l'échantillon m_s.

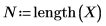
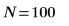
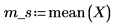
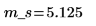
3. Définissez le niveau de signification, l'écart-type de population et la moyenne de population proposée.

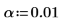
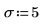
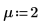
4. Calculez le score z.

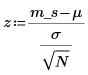
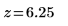
5. Indiquez les hypothèses nulle et alternative pour un test bilatéral.

H0: m = μ

H1: m ≠ μ

6. Utilisez la fonction pnorm pour calculer la valeur p et tester l'hypothèse. Dans cet exemple, l'évaluation est de 1 pour toutes les expressions booléennes lorsque l'hypothèse nulle est vraie (vous ne rejetez pas H0).

<region id="ID0EPGKBB" top="883.20000000000016" left="38.400000000000006" height="25.6" width="185.36333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">P</id>
      <apply>
        <mult />
        <real>2</real>
        <parens>
          <apply>
            <minus />
            <real>1</real>
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pnorm</id>
              <sequence>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
                <real>0</real>
                <real>1</real>
              </sequence>
            </apply>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

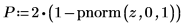
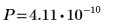
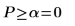
La probabilité pour que les statistiques du test soient supérieures à celles observées est de 4.11*10-10, en supposant que l'hypothèse nulle soit vraie. La comparaison entre la valeur p et le niveau de signification indique qu'il est prouvé que l'hypothèse alternative est vraie.

7. Utilisez la fonction qnorm pour calculer les limites de la région critique et tester l'hypothèse.

<region id="ID0E4JKBB" top="1171.2000000000003" left="38.400000000000006" height="47.2" width="163.91666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="90">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">crit</id>
      <apply>
        <absval />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qnorm</id>
          <sequence>
            <apply>
              <div />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
              <real>2</real>
            </apply>
            <real>0</real>
            <real>1</real>
          </sequence>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

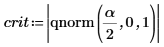
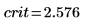
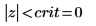
Rejetez l'hypothèse nulle. Il est évident que la moyenne est différente de μ.

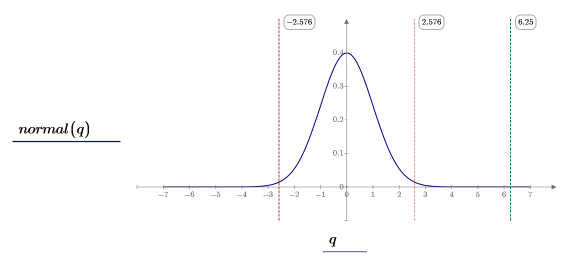
8. Utilisez la fonction dnorm pour calculer et tracer la distribution normale standard (bleu), les frontières de la région critique (rouge) et le score z (vert).

<region id="ID0EHNKBB" top="1382.4" left="38.400000000000006" height="25.6" width="196.62333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="96">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">normal</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">q</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">dnorm</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">q</id>
          <real>0</real>
          <real>1</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Rubriques associées

Loi normale

Est-ce que cela a été utile ?