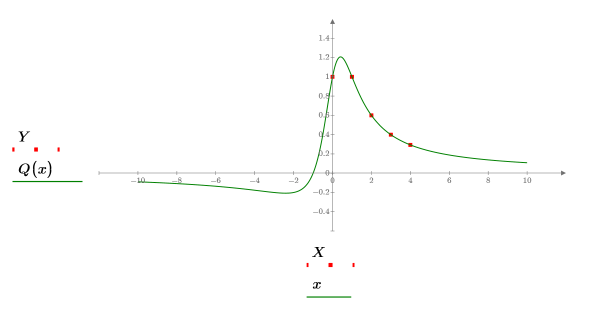
Exemple : Interpolation de Thiele
Effectuez une interpolation de fraction continue de Thiele sur un jeu de données.
Thielecoeff et Thiele
Les fonctions Thielecoeff et Thiele permettent d'interpoler un ensemble de données provenant d'une fonction rationnelle.
1. Définissez le nombre de points d'interpolation.
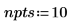
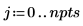
2. Définissez une fonction rationnelle, comme la fonction Lorentzian.
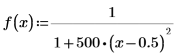
3. Prenez des échantillons de la fonction et enregistrez leurs valeurs x et y dans des vecteurs.
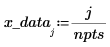
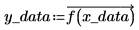
4. Utilisez la fonction Thielecoeff pour trouver les coefficients de la fraction continue qui correspondent aux points échantillonnés.
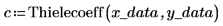
5. Appelez la fonction Thiele pour effectuer l'interpolation.
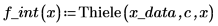
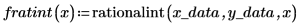
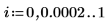
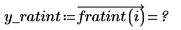
Les fonctions Thiele sont correctes, mais la fonction rationalint échoue pour certains points de la plage d'interpolation. Ceci s'explique par le fait que les données sont symétriques, ce qui entraîne des erreurs de division par zéro au niveau de certaines valeurs intermédiaires x :
6. Tracez la fonction d'origine, les points échantillonnés et la courbe interpolée.
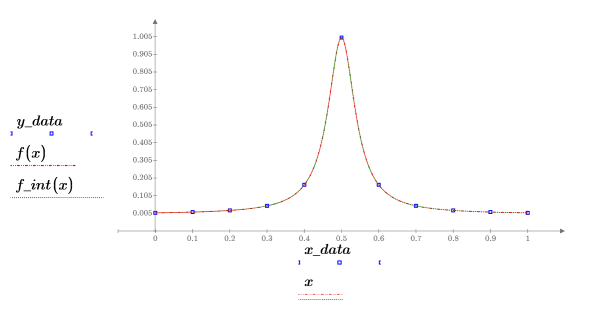
7. Tracez un graphique montrant les valeurs résiduelles de l'interpolation Thiele.
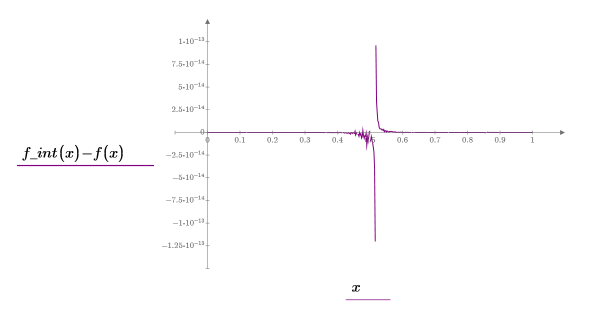
Ordre des points
L'algorithme échoue à renvoyer les valeurs correctes si deux points adjacents ont des valeurs y identiques. Vous devez réordonner les données pour obtenir le résultat correct.
1. Définissez un jeu de points.
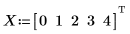
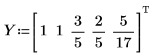
2. Trouvez les coefficients de la fonction Thiele.
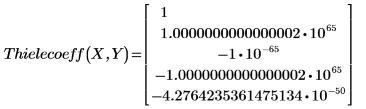
Les coefficients sont trop grands.
3. Réordonnez les données pour obtenir une solution adéquate.
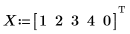
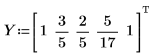
4. Répétez l'étape 2.
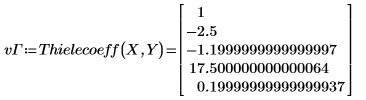
5. Définissez la fonction interpolée.
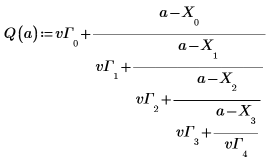
Tracez la fonction interpolée et les points de données d'origine.