Exemple : Résolution d'un système d'équations linéaires
Résolvez un système linéaire d'équations n à n inconnues en utilisant la fonction lsolve ou des blocs de résolution.
Utilisation de lsolve
1. Supposons que vous disposez de l'ensemble d'équations suivant (défini avec l'opérateur égal à) :
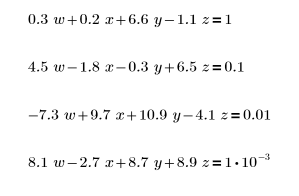
2. Créez une matrice non singulière correspondant au système d'équations ci-dessus :

3. Créez le vecteur de constantes correspondant au système d'équations ci-dessus :
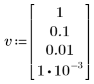
4. Utilisez la fonction lsolve pour trouver la solution :
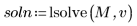
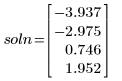
Utilisation des blocs de résolution
Vous pouvez également résoudre le système d'équations en utilisant un bloc de résolution.
Si vous déclarez le système comme étant la matrice multipliée par un vecteur X, vous devez résoudre toutes les variables du vecteur en une seule fois. Les éléments du vecteur ne peuvent pas être gardés constants dans cette formulation. |
1. Fournissez un vecteur X de valeurs initiales :
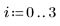
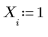
2. Insérez un bloc de résolution, puis utilisez la fonction Find pour résoudre le système d'équations ci-dessus :

Le vecteur X de valeurs initiales doit être défini avant et à l'extérieur du bloc de résolution. |
Blocs de résolution - Résolution pour les matrices
1. Définissez l'équation algébrique de Riccati (issue de la théorie des systèmes et des asservissements) :
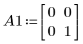
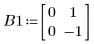
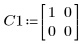
2. Définissez la matrice des hypothèses initiales comme matrice unité :
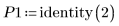
3. Utilisez la fonction Find pour résoudre l'ensemble d'équations ci-dessus :
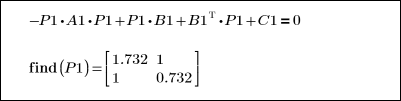
Unités des blocs de résolution
1. Configurez V1, V2 et V3 sur 1 volt :
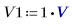
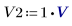
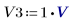
2. Définissez et résolvez le système d'équations à trois inconnues :
