Exemple : Fenêtrage de signal
Utilisez les fonctions suivantes pour effectuer le fenêtrage de signal :
Réponse impulsionnelle passe-bas idéale / tronquée
1. Définissez la réponse impulsionnelle h d'un filtre passe-bas idéal avec une fréquence de coupure normalisée de 0.15.
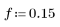
2. Définissez la réponse impulsionnelle.
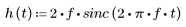
Etant donné qu'un filtre opérationnel, de longueur finie, doit avoir une réponse impulsionnelle finie, cette réponse idéale est tronquée à un certain nombre gérable de termes.
3. Pour vérifier l'effet de la troncation directe sans fenêtrage de la réponse en fréquence, définissez un filtre de longueur N composé simplement des N termes centraux de la réponse idéale, décalé de manière à rendre le filtre causal.
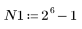
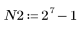
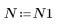
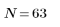
En guise d'exercice, définissez N à N2 et observez l'effet d'une augmentation du nombre de termes dans les exemples ci-dessous.
4. Appliquez la fonction de réponse impulsionnelle sur la plage de termes et tracez la fonction résultante.
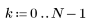
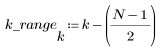
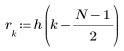
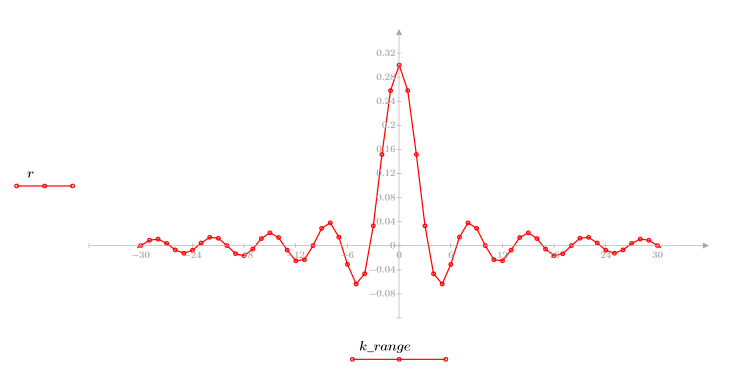
5. Calculez la réponse en fréquence pour ce signal tronqué en utilisant la fonction gain, après avoir défini la plage de fréquences (multiples de la fréquence de l'échantillon).
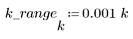
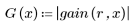
6. Collectez les amplitudes discrètes de la fonction gain dans un nouveau tableau.
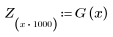
7. Déterminez l'amplitude maximale de G ainsi que la fréquence correspondante.
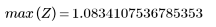
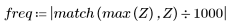
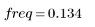
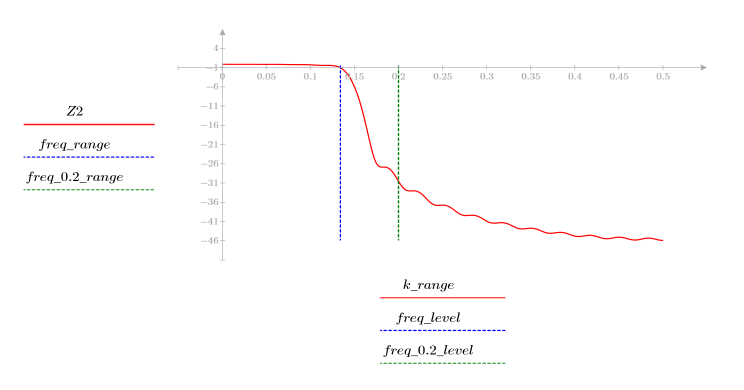
Lorsque le nombre de termes N1=63, le gain maximum 1.083 se produit à la fréquence freq=0.134.
Lorsque le nombre de termes N2=127, le gain maximum 1.092 se produit à la fréquence freq=0.142, en se déplaçant par conséquent vers l'extrémité de la bande passante.
A la fréquence freq=0.2, le gain chute à une valeur presque nulle. Comparez le gain au voisinage de cette fréquence dans chacun des exemples ci-dessous.
8. Tracez la fonction gain sur la plage définie et déterminez la fréquence à laquelle l'amplitude est maximale.
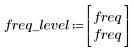
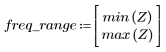
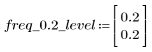
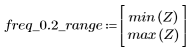
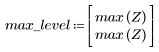
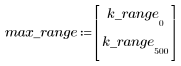
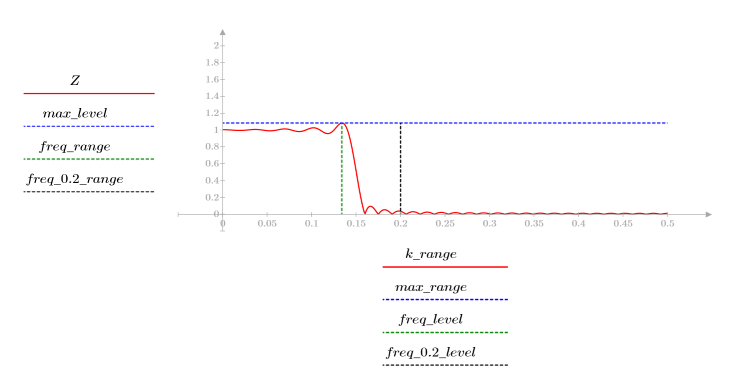
Le dépassement à l'extrémité de la bande passante est connu sous le nom de phénomène de Gibbs. L'augmentation de l'ordre N du filtre de N1=63 à N2=127 comme ci-dessus déplace le dépassement plus près de l'extrémité de la bande passante, mais ne diminue pas son amplitude.
La transition de 1 à 0 devient plus nette avec l'augmentation de la valeur de l'ordre N du filtre.
Un moyen permettant de produire une réponse en fréquence plus souhaitable consiste à fenêtrer la réponse impulsionnelle idéale, afin que la transition à 0 au niveau des extrémités de la réponse impulsionnelle du filtre se fasse de manière plus douce. Les fenêtres sont multipliées terme à terme avec un vecteur réponse r.
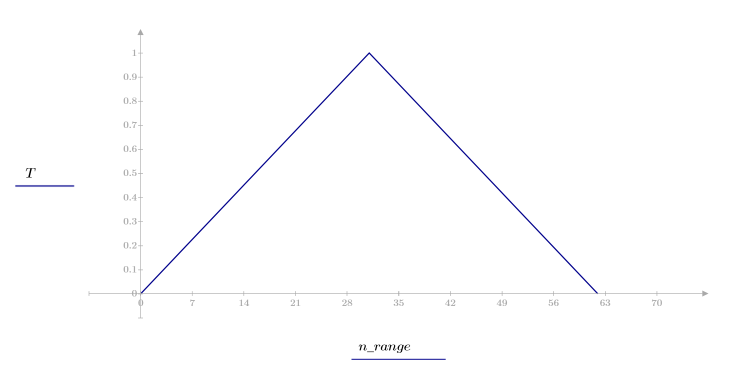
Fenêtre triangulaire
La fonction triangular renvoie la fenêtre triangulaire ou la fenêtre de Bartlett de largeur N.
L'élément j du vecteur obtenu est donné par :
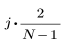
pour
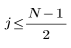
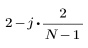
pour
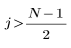
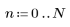
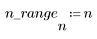
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
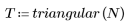
2. Calculez la réponde d'impulsion fenêtrée.
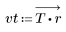
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vt, à la fréquence k/1000.
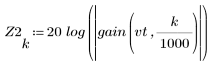
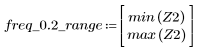
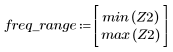
Fenêtre de Hanning
La fonction hanning renvoie la fenêtre de Hanning de largeur N.
L'élément k du vecteur obtenu est donné par :
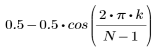
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
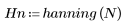
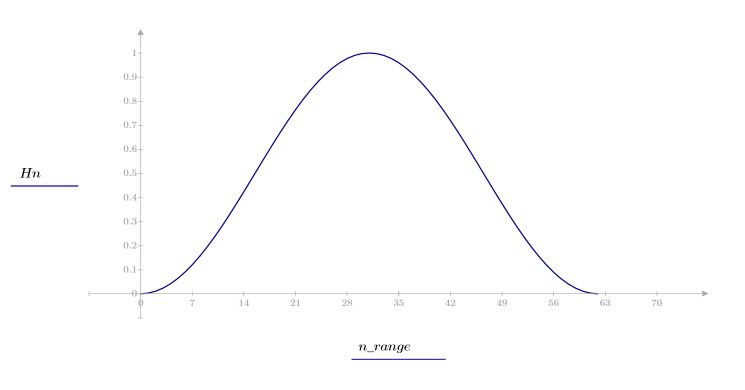
2. Calculez la réponde d'impulsion fenêtrée.
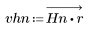
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vhn, à la fréquence k/1000.
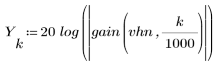
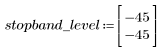
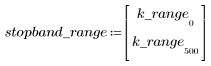
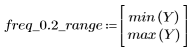
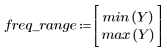
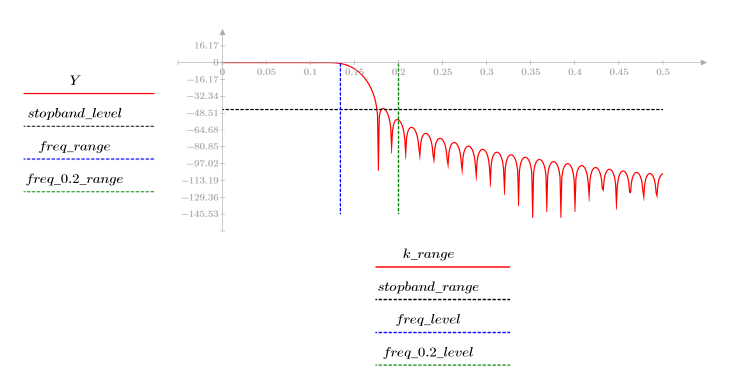
L'ondulation de la bande de coupure est d'environ -45 dB.
Fenêtre de Hamming
La fonction hamming renvoie la fenêtre de Hamming de largeur N.
L'élément k du vecteur obtenu est donné par :
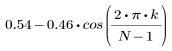
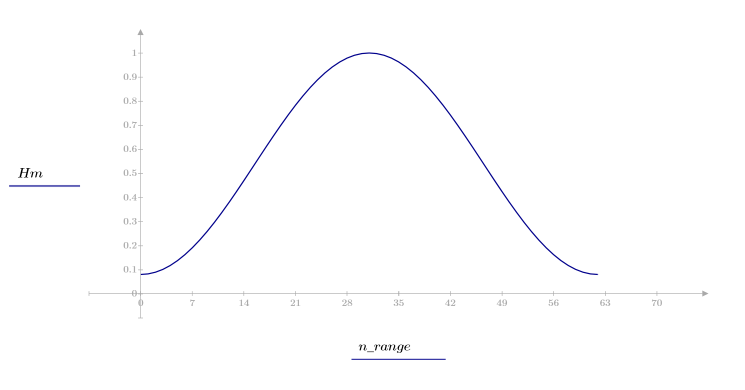
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
2. Calculez la réponde d'impulsion fenêtrée.
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vhm, à la fréquence k/1000.
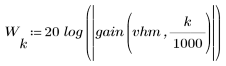
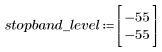
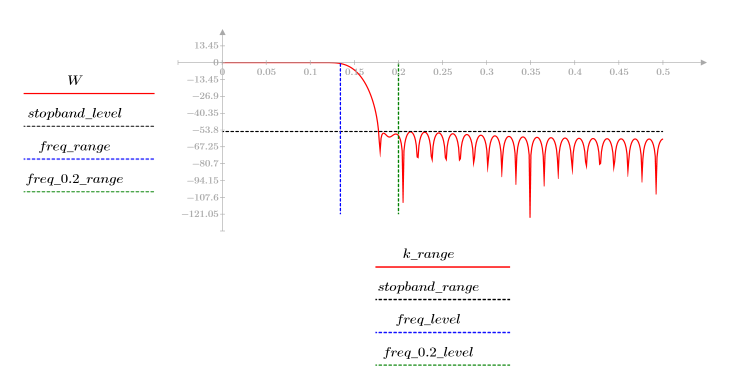
L'ondulation de la bande de coupure est d'environ -55 dB.
Fenêtre de Blackman
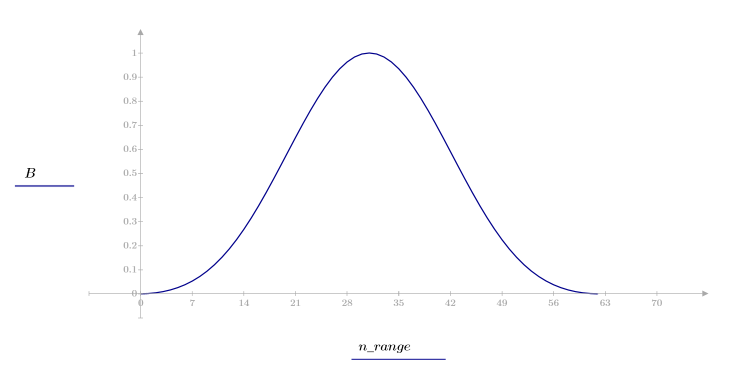
La fonction blackman renvoie la fenêtre de Blackman de largeur N.
L'élément k du vecteur obtenu est donné par :
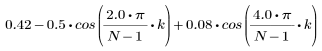
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
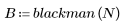
2. Calculez la réponde d'impulsion fenêtrée.
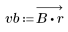
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vb, à la fréquence k/1000.
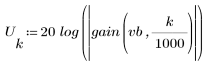
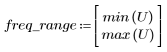
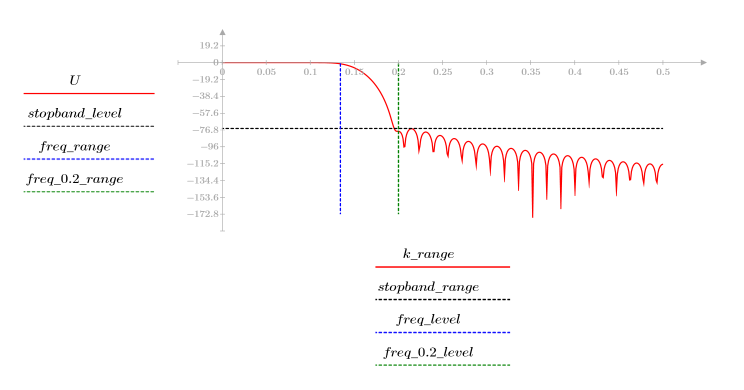
L'ondulation de la bande de coupure est d'environ -75 dB.
Fenêtre de Nuttall
La fonction nuttall renvoie la fenêtre de Nuttall de largeur N.
L'élément k du vecteur obtenu est donné par :
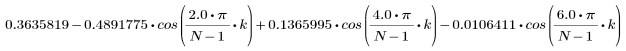
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
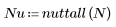
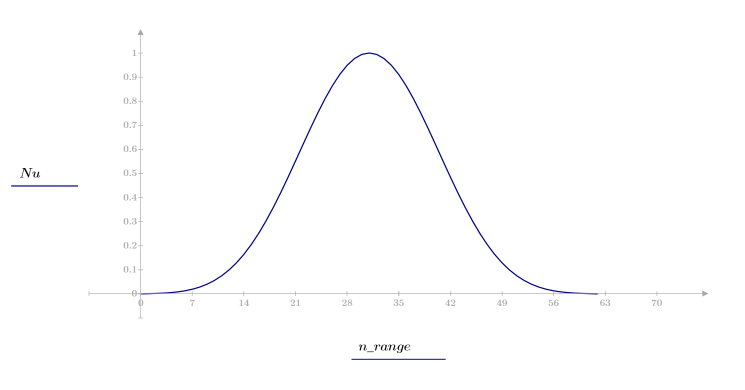
2. Calculez la réponde d'impulsion fenêtrée.
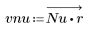
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vnu, à la fréquence k/1000.
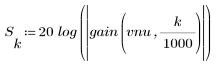
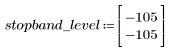
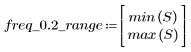
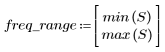
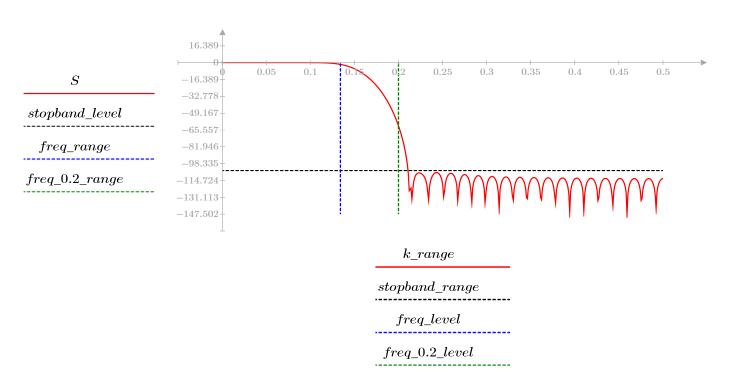
L'ondulation de la bande de coupure est d'environ -105 dB.
Fenêtre rectangulaire adoucie
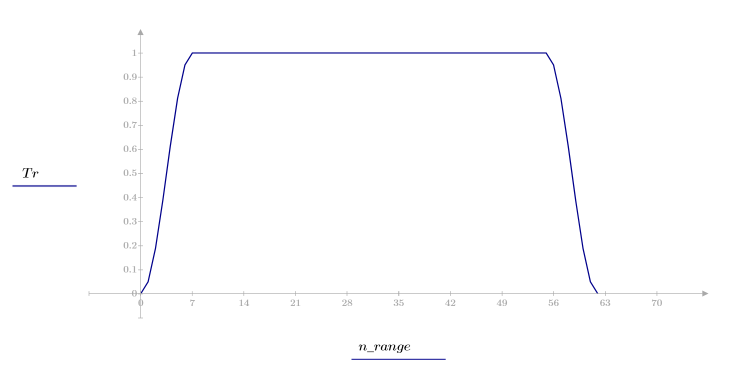
La fonction taprect renvoie la fenêtre rectangulaire adoucie de largeur N.
Cette fenêtre est horizontale en son milieu avec une hauteur de 1 et des extrémités adoucies suivant des courbes en cosinus. Les côtés droit et gauche utilisent les valeurs :
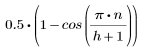
où
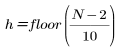
et n prend les valeurs comprises entre 0 et h.
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
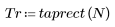
2. Calculez la réponde d'impulsion fenêtrée.
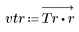
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vtr, à la fréquence k/1000.
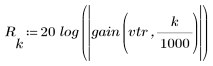
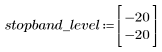
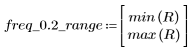
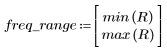
Fenêtre de Gauss
La fonction gaussian renvoie la fenêtre de Gauss de largeur N et de paramètre a. Le nombre a est un nombre réel proportionnel à l'inverse de la variance gaussienne et doit satisfaire la condition suivante : 2 < a < 20.
L'élément k du vecteur obtenu est donné par :
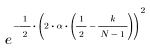
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
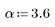
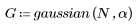
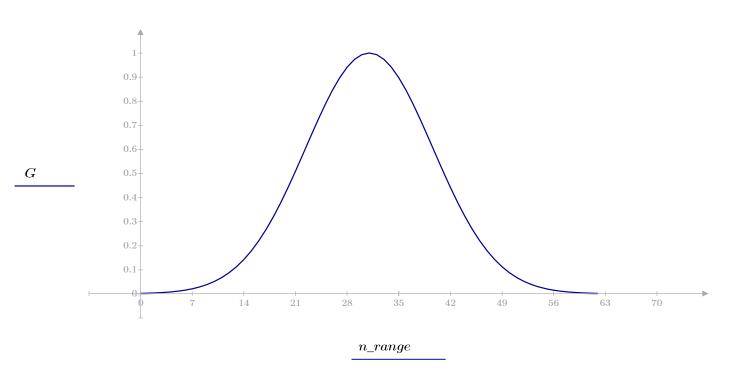
2. Calculez la réponde d'impulsion fenêtrée.
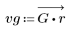
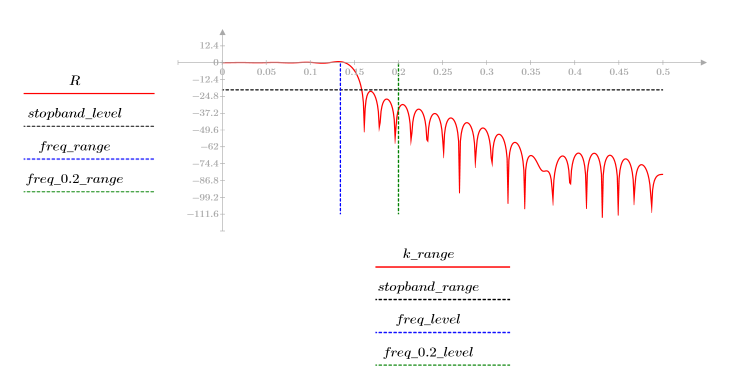
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vg, à la fréquence k/1000.
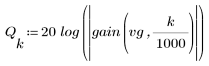
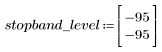
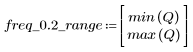
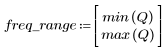
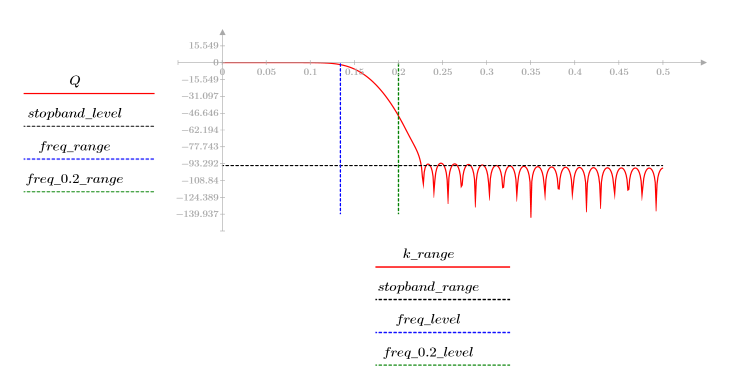
L'ondulation de la bande de coupure est d'environ -95 dB.
Fenêtre de Kaiser
La fonction kaiser renvoie la fenêtre de Kaiser de largeur N et de paramètre b. Le paramètre b doit satisfaire la condition suivante : 2≤b≤20.
L'élément k du vecteur obtenu est donné par :
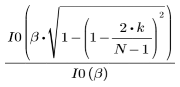
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
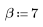
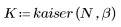
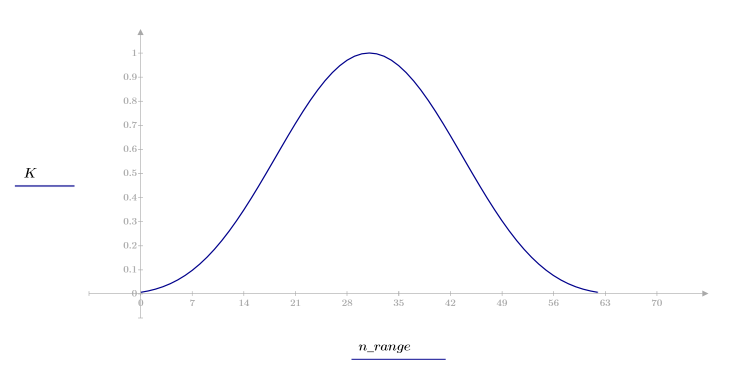
2. Calculez la réponde d'impulsion fenêtrée.
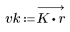
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vk, à la fréquence k/1000.
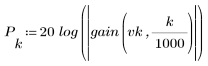
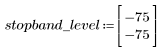
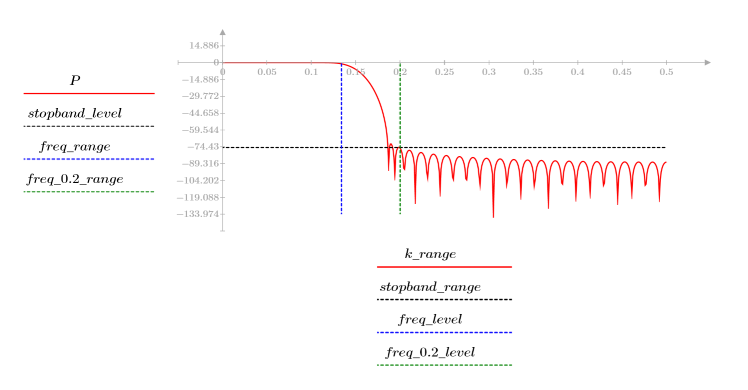
L'ondulation de la bande de coupure est d'environ -75 dB.
Fenêtre de Chebyshev
La fonction cheby renvoie la fenêtre de Chebyshev ou une fenêtre d'ondulation équivalente de largeur N et de paramètre b. Le paramètre b spécifie l'amplitude de l'ondulation latérale maximale en dB et doit satisfaire la condition suivante : 1 < b ; en général b > 50. La longueur de cette fenêtre doit être impaire. La fenêtre de Chebyshev est calculée en prenant la transformée de Fourier discrète inverse d'un polynôme de Chebyshev évalué à des points situés sur le cercle unitaire. Voir "Programs for Digital Signal Processing" (IEEE Press) pour plus d'informations sur cette fenêtre.
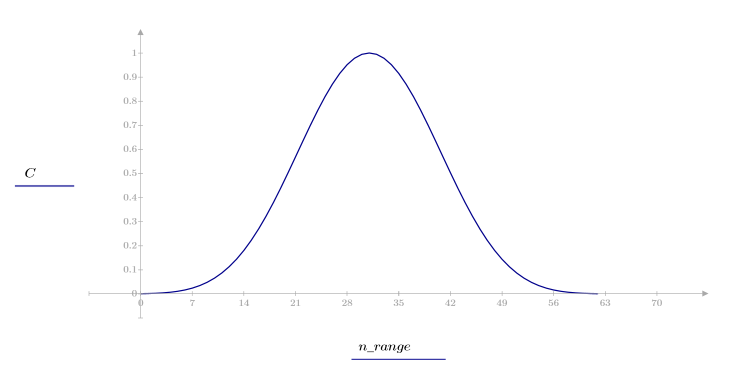
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
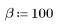
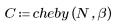
2. Calculez la réponde d'impulsion fenêtrée.
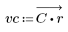
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vc, à la fréquence k/1000.
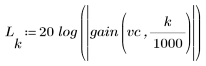
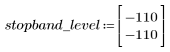
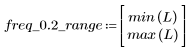
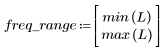
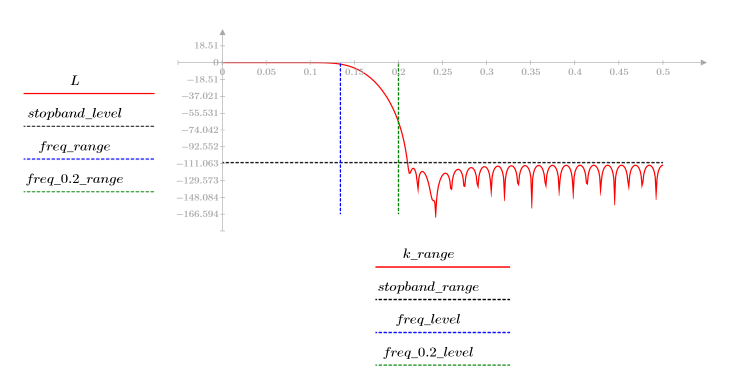
L'ondulation de la bande de coupure est d'environ -110 dB.
Fenêtre en cosinus surélevé
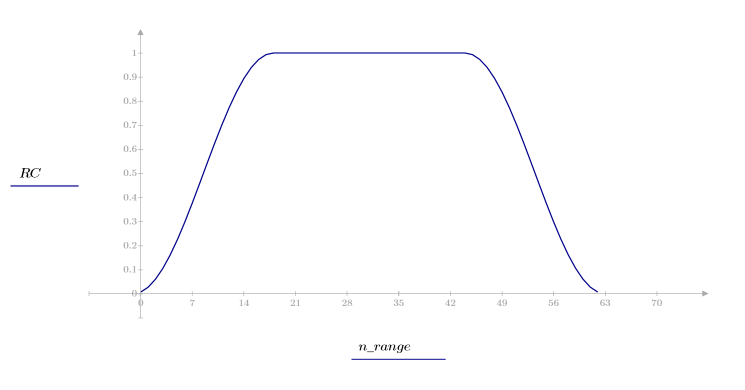
La fonction costaper est similaire à la fonction taprect en ce sens qu'elle renvoie une fenêtre rectangulaire présentant des extrémités adoucies suivant une courbe en cosinus. Vous pouvez toutefois utiliser le paramètre a pour spécifier le pourcentage de la fenêtre devant être créé à l'aide d'une courbe en cosinus. Le paramètre a doit être compris entre 0 et 1 ; une valeur égale à 0 renvoie une fenêtre rectangulaire, tandis qu'une valeur égale à 1 renvoie une courbe en cosinus surélevé.
En ce qui concerne la partie adoucie de la fenêtre, la valeur du kième élément est donnée par :
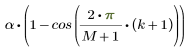
où M est le nombre d'éléments de la fenêtre inclus dans l'une des extrémités, et est donné par a-N :
1. Appliquez la fonction à l'ordre de filtrage N et tracez le vecteur obtenu.
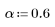
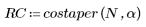
2. Calculez la réponde d'impulsion fenêtrée.
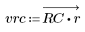
3. Utilisez la fonction gain pour calculer et tracer le gain en dB de ce filtre, avec des coefficients vrc, à la fréquence k/1000.
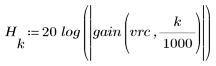
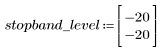
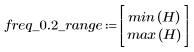
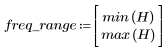
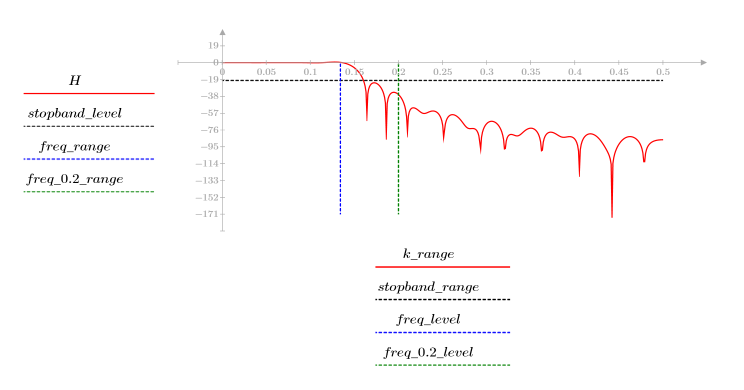
L'ondulation de la bande de coupure est d'environ -20 dB.
Documents de référence
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications, Prentice-Hall (1987).
• Lawrence R. Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, Inc. (1975).
• T. W. Parks and C. S. Burrus, Digital Filter Design, Wiley-Interscience (1987).