Exemple : Régression de fonction rationnelle 2
rationalfitnp - Absence de pôles
Utilisez les fonctions rationalfit et rationalfitnp pour réaliser une régression de fonction rationnelle. Lorsque vous utilisez la fonction rationalfitnp au lieu de la fonction rationalfit, la solution au problème traditionnel des moindres carrés consiste à vérifier les racines du dénominateur dans l'intervalle d'ajustement. En l'absence de pôles, l'ajustement généré est renvoyé. En présence de pôles, des contraintes supplémentaires sont ajoutées au problème d'optimisation non linéaire.
1. Définissez un jeu de données en modifiant légèrement la fonction inverse de x.
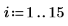
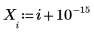
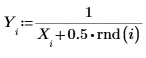
2. Indiquez un ordre pour le numérateur et le dénominateur de la fonction rationnelle.
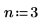
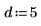
La fonction d'ajustement a la forme suivante :
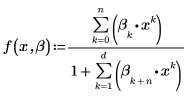
3. Définissez une délimitation de confiance et un vecteur des écarts-types.
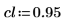
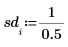
4. Appelez les fonctions rationalfit et rationalfitnp.
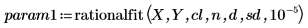 | 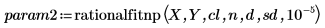 |
 |  |
Pour param1 et param2, la première colonne contient les paramètres et les autres colonnes contiennent les délimitations supérieure et inférieure de chaque paramètre à la limite de confiance définie ci-dessus.
5. Tracez le jeu de données et les deux courbes de régression.
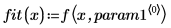
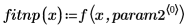
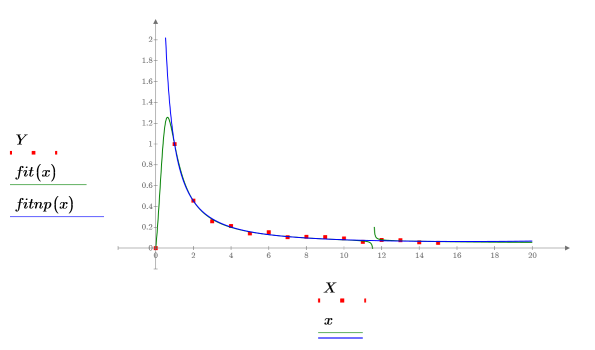
Le pôle a été supprimé par la fonction rationalfitnp. Son polynôme dénominateur est de la forme suivante :
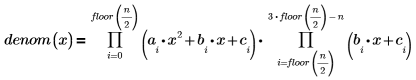
Pour éviter le pôle, les contraintes suivantes ont été ajoutées :
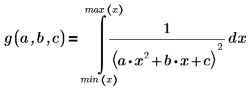
 | 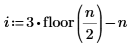 |
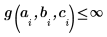 | 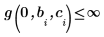 |
LeastSquaresFit
Comparez les courbes d'ajustement renvoyées par rationalfitnp et LeastSquaresFit. La fonction LeastSquaresFit exécute le même algorithme que celui de rationalfitnp. Elle nécessite toutefois les valeurs initiales et les limites de confiance des paramètres. Vous pouvez effectuer cette opération lorsque vous voulez que le terme constant soit dans le numérateur et non dans le dénominateur.
1. Définissez la fonction d'ajustement.
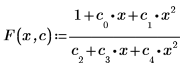
2. Définissez les valeurs initiales des paramètres.
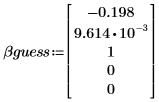
3. Définissez les conditions aux limites supérieure et inférieure des paramètres.

4. Appelez la fonction LeastSquaresFit.
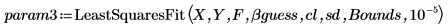
5. Tracez le jeu de données et les courbes d'ajustement renvoyées par les fonctions rationalfitnp et LeastSquaresFit.
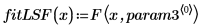
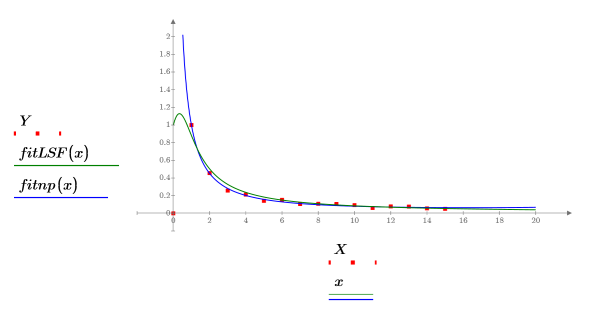
Toute méthode de filtrage ou de transformation des données qui oriente les données vers une ligne droite avant tout ajustement de fonction rationnelle, ajoute une vitesse de convergence considérable à la fonction rational et peut avoir pour effet d'éliminer les pôles indésirables. |