Exemple : Tracés quantile-quantile

Fonctions > Statistiques > Statistiques graphiques > Exemple : Tracés quantile-quantile

Utilisez la fonction qqplot pour représenter des tracés quantile-quantile (Q-Q).

Deux jeux de données

Comparez les quantiles de deux jeux de données dans un tracé Q-Q afin de vérifier si leur distribution est identique.

1. Définissez un jeu de données.

La colonne 2 indique le lot dans lequel la mesure a été effectuée et la colonne 3 indique la puissance mesurée en bars de nitrate Si.

2. Extrayez les deux colonnes concernées, 2 et 3.

<region id="ID0EQFVAB" top="345.6" left="38.400000000000006" height="25.6" width="377.50000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="156">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">BatchData</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">submatrix</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
          <real>0</real>
          <apply>
            <minus />
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">rows</id>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Data</id>
            </apply>
            <real>1</real>
          </apply>
          <real>2</real>
          <real>3</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

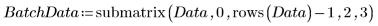
3. Appelez vlookup pour diviser les données en fonction de l'endroit où ont été effectuées les mesures du lot 1 ou 2.

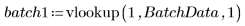
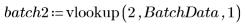
4. Calculez le premier et le troisième quartiles de chaque lot.

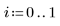
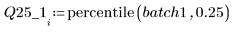
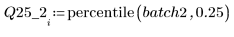
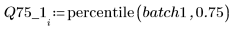
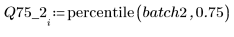
5. Tracez le tracé Q-Q et les quantiles.

<region id="ID0ENOVAB" top="806.40000000000009" left="19.200000000000003" height="552" width="593.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="178">
          <traceStyle color="#FF800080" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="179">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="180">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="181">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="182">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="183">
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="474.799999999999" height="360" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="345" end="845">
          <axisLine position="bottom" positionticmark="-1" legendWidth="335.533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="184">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="185">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="186">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="187">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="188">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_2</id>
              </math>
              <math resultRef="189">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="190">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_2</id>
              </math>
              <math resultRef="191">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="192">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="193">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="345" end="845">
          <axisLine position="left" positionticmark="-1" legendWidth="95.5333333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="194">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">qq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="195">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="198">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="199">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="200">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="201">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="202">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q25_1</id>
              </math>
              <math resultRef="203">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Q75_1</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

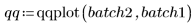
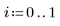
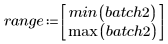
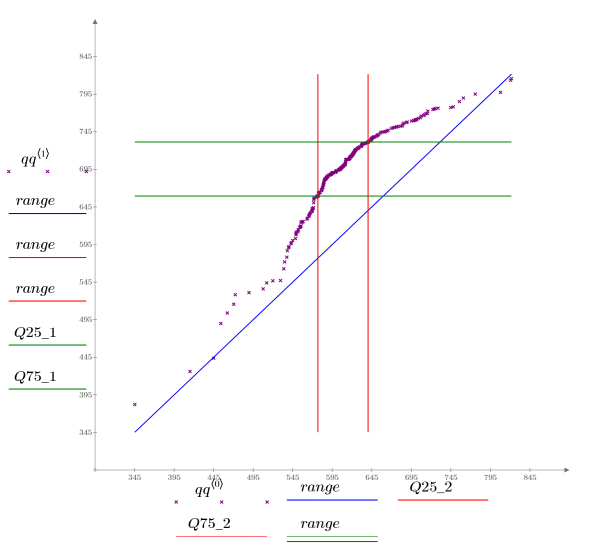
Une ligne de référence 1 à 1 est tracée de manière à mettre en évidence la façon dont les données varient.

Le tracé Q-Q indique que les deux lots ne partagent pas la même distribution, bien que les valeurs pour les centiles très petits et très grands soient similaires. Les quantiles du lot 1 sont nettement supérieurs à ceux du lot 2, ce qui est caractéristique de conditions de traitement très différentes.

Loi normale

Déterminez si les mesures d'un fluxmètre thermique ont été réalisées de façon aléatoire. Vérifiez si les mesures sont normalement distribuées en les comparant avec la distribution normale dans un tracé Q-Q.

1. Définissez un ensemble de données qui décrit le flux thermique.

2. Trouvez les points de données du tracé Q-Q normal.

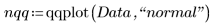
3. Trouvez la ligne de l'ajustement optimal afin de déterminer la proximité des quantiles de données avec les quantiles de distribution normale.

<region id="ID0EIUVAB" top="2016.0000000000002" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="234">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

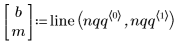
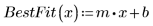
4. Tracez le tracé Q-Q et la ligne de meilleur ajustement.

<region id="ID0EZVVAB" top="2092.8" left="19.200000000000003" height="312" width="590.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="236">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="237">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="394.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="9.15" end="9.4">
          <axisLine position="origin" positionticmark="5" legendWidth="91.2633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="244">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="245">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="239">
              <real xmlns="http://schemas.mathsoft.com/math50">9.15</real>
            </startValue>
            <secondTickValue resultRef="241">
              <real xmlns="http://schemas.mathsoft.com/math50">9.20</real>
            </secondTickValue>
            <endValue resultRef="243">
              <real xmlns="http://schemas.mathsoft.com/math50">9.35</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-3.5" end="3.5">
          <axisLine position="left" positionticmark="-1" legendWidth="157.56" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="246">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">nqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="247">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="248">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">nqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="249">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

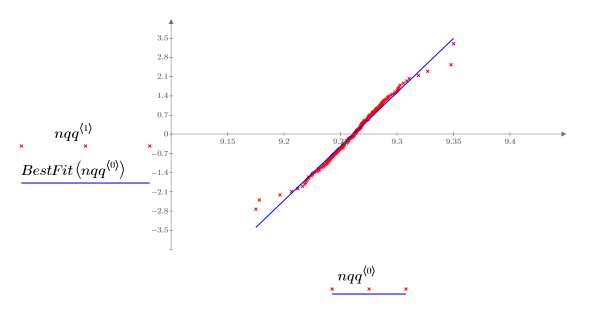
La corrélation très proche avec la ligne de référence indique que les échantillons sont normalement distribués.

La vérification de cette normalité est l'un des tests réalisés lors de la détection des valeurs extrêmes.

Loi de Weibull

Vérifiez si un jeu de données suit une distribution Weibull.

1. Enregistrez dans le vecteur R les tensions de dysfonctionnement de l'isolation électrique pour les câbles qui sont soumis à des contraintes de tension croissantes.

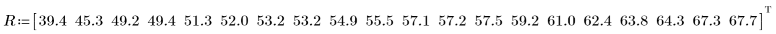
2. Tracez un histogramme des données.

<region id="ID0EF2VAB" top="2880.0000000000005" left="19.200000000000003" height="312" width="589.906666755675" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="267">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <graph-size width="470.706666755675" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="32.5" end="72.5">
          <axisLine position="origin" positionticmark="0" legendWidth="115.576666666667" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="270">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <plus />
                  <id xml:space="preserve">bins</id>
                  <real>2.5</real>
                </apply>
              </math>
              <math resultRef="271">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="269">
              <real xmlns="http://schemas.mathsoft.com/math50">37.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="5">
          <axisLine position="left" positionticmark="-1" legendWidth="85.6133333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="272">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">stem</id>
              </math>
              <math resultRef="273">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

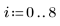
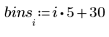
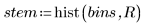
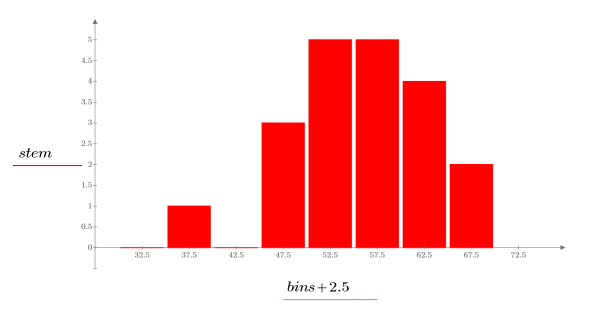
L'histogramme indique que les données n'obéissent pas à une distribution normale. Les données sont asymétriques. Vous pouvez comparer les données à une distribution de Weibull dans un tracé Q-Q.

3. Trouvez les points de données pour le tracé Q-Q de Weibull.

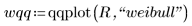
4. Trouvez la ligne d'ajustement optimal afin de déterminer la proximité des quantiles de données avec les quantiles à distribution de Weibull.

<region id="ID0E15VAB" top="3494.4000000000005" left="38.400000000000006" height="25.6" width="152.6866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="283">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">BestFit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
        </boundVars>
      </function>
      <apply>
        <plus />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
        </apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">b</id>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="round-trip-decimal-places" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

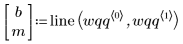
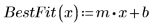
5. Tracez le tracé Q-Q et la ligne de meilleur ajustement.

<region id="ID0ELAWAB" top="3571.2000000000007" left="19.200000000000003" height="312" width="592.999999999999" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="285">
          <traceStyle color="#FFFF0000" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="286">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="396.999999999999" height="235.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="3.6" end="4.3">
          <axisLine position="origin" positionticmark="8" legendWidth="93.3466666666667" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="293">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>0</real>
                </apply>
              </math>
              <math resultRef="294">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="288">
              <real xmlns="http://schemas.mathsoft.com/math50">3.60</real>
            </startValue>
            <secondTickValue resultRef="290">
              <real xmlns="http://schemas.mathsoft.com/math50">3.7</real>
            </secondTickValue>
            <endValue resultRef="292">
              <real xmlns="http://schemas.mathsoft.com/math50">4.3</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-6.4" end="2.4">
          <axisLine position="left" positionticmark="-1" legendWidth="159.643333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="295">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve">wqq</id>
                  <real>1</real>
                </apply>
              </math>
              <math resultRef="296">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="297">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">BestFit</id>
                  <apply>
                    <matcol />
                    <id xml:space="preserve">wqq</id>
                    <real>0</real>
                  </apply>
                </apply>
              </math>
              <math resultRef="298">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

La corrélation avec la ligne de référence indique que le jeu de données peut être modélisé à l'aide d'une distribution de Weibull.

Pour les tracés Q-Q de Weibull, une échelle logarithmique est utilisée.

Référence

Lawless, J.F., Statistical Methods for Lifetime Data, 2nd ed, Wiley-Interscience, 2002.

Rubriques associées

Tracé quantile-quantile

Est-ce que cela a été utile ?