Exemple : Analyse de composant principal 2
Utilisez les fonctions Nipals et Nipals2 pour analyser des données complexes telles que les spectres du proche infrarouge (NIR) de comprimés pharmaceutiques avec cinq dosages différents des ingrédients actifs (les données sont fournies avec l'aimable autorisation de Bruker Optics, Inc.). Vous pouvez créer un modèle permettant de distinguer chaque dosage en fonction de son spectre, même si les dosages réels ne sont pas connus. Ce modèle peut être utilisé à des fins de contrôle de la qualité lors de la fabrication ultérieure des comprimés.
1. Définissez le jeu de données suivant :
|
|
Cet ensemble de données décrit une étude en double aveugle dans un essai clinique.
|

La première colonne est le nombre d'onde (1/longueur d'onde) en cm-1. Il y a cinq spectres séquentiels de chaque dosage, constituant les 25 colonnes restantes.
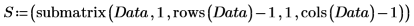
3. Utilisez les fonctions max et match pour trouver la valeur maximale et le spectre qui la contient. Dans la mesure où les valeurs de données sont très petites, définissez TOL sur une valeur plus petite.
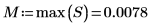
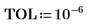
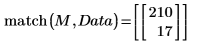
La valeur maximale est dans la ligne 210 et la colonne 17 de la matrice de données.
4. Tracez les deux premiers spectres de chaque dosage, ce qui fait un total de 10 jeux de données. Les paires de jeux de données sont les colonnes [1,2], [6,7], [11,12], [16,17] et [21,22] de la Data matrice.
◦ Pour obtenir une échelle raisonnable pour l'axe horizontal, divisez les nombres d'onde par 1000. De même, étant donné que les valeurs du spectre sont petites, nous les multiplions par 1000.
◦ Utilisez un marqueur horizontal pour afficher la valeur maximale des spectres.
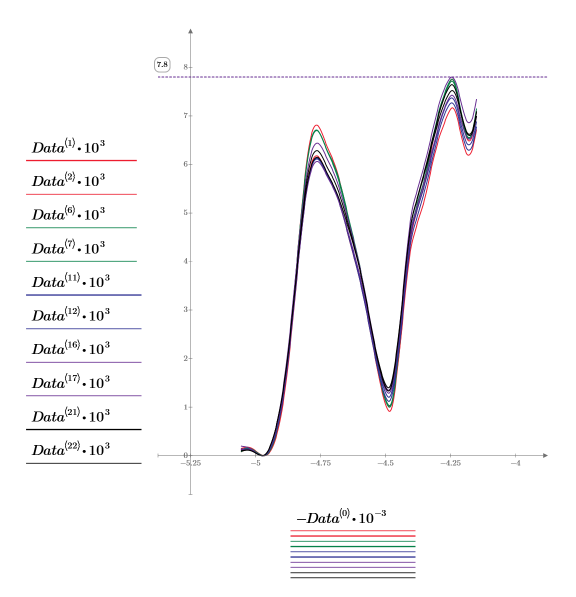
◦ Par convention, les nombres d'onde sont tracés en ordre décroissant. Data<0> est par conséquent inversé pour afficher les nombres d'onde dans le bon ordre.
◦ Aucune partie du spectre ne peut servir à distinguer aisément un dosage d'un autre : ils ont tous le même format de base et des valeurs d'absorbance proches.
◦ La plupart des données sont redondantes. Chaque spectre contient 236 points, ce qui représente 236 variables mesurées (absorbance pour une longueur d'onde particulière de la lumière), mais la variation de ces points est clairement interdépendante.
5. Divisez la matrice Data en deux jeux de données, à savoir les nombres d'onde (colonne 0) et les spectres de chaque comprimé (sous-matrice S). En vue de respecter la convention habituellement utilisée, transposez les spectres de chaque comprimé de telle sorte que chaque colonne corresponde à une variable indépendante.
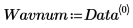
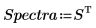
6. Définissez le nombre de composants principaux, ainsi que le nombre maximal d'itérations, avant d'appliquer la fonction Nipals aux données. La fonction Nipals centre les données, en soustrayant le spectre moyen de chaque ligne.
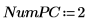
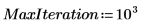
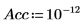
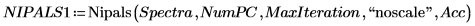
7. Choisissez un spectre à reconstruire.
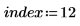
8. Extrayez les scores et les influences du résultat de la fonction Nipals.
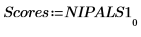
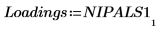
9. Utilisez la fonction mean pour calculer le spectre moyen.
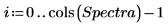
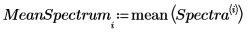
10. Estimez le spectre d'origine en multipliant la matrice des vecteurs d'influences par la matrice des scores, puis en ajoutant le spectre moyen.
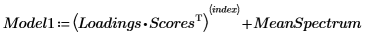
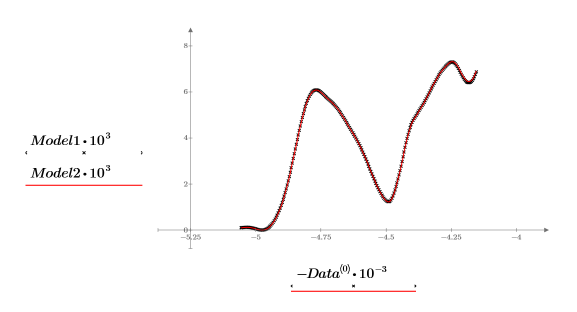
11. Tracez le spectre d'origine et le spectre reconstruit. Mettez à l'échelle les axes horizontal et vertical pour obtenir des valeurs raisonnables.
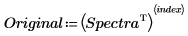
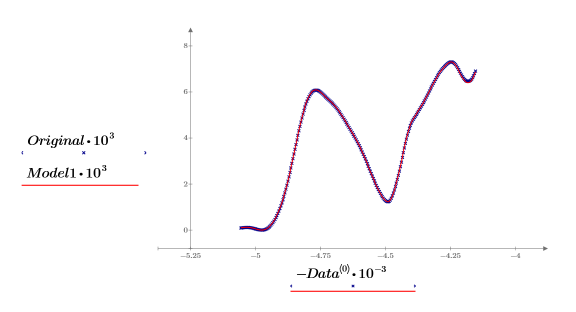
Tous les spectres sont correctement représentés à l'aide de deux composants principaux uniquement pour l'analyse de composant principal.
12. Réarrangez les scores dans deux matrices. Chaque colonne des matrices représente les scores d'un des cinq dosages des comprimés.
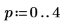
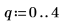
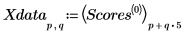
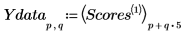
13. Tracez les scores du premier facteur en fonction des scores du deuxième facteur. Chaque dosage est représenté dans une couleur différente.
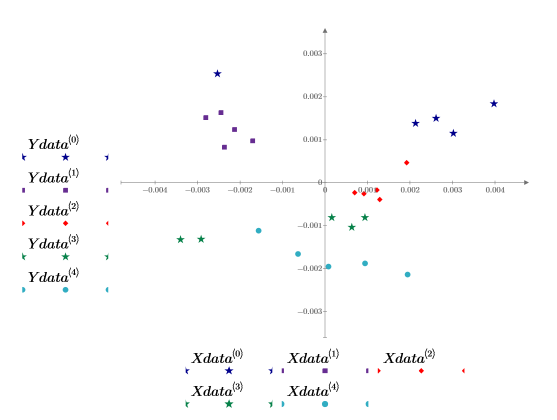
Un certain regroupement des données est évident, mais il reste difficile de distinguer un dosage d'un autre. L'ajout d'un troisième score au tracé peut peut-être vous aider.
14. Utilisez la fonction Nipals2 pour ajouter quatre composants principaux au modèle créé avec deux composants principaux.
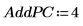
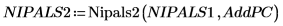
La matrice de sortie de NIPALS2 a la même forme que celle de NIPALS, mais avec des colonnes et des lignes supplémentaires correspondant aux composants principaux qui ont été ajoutés. Le nombre de scores et d'influences est maintenant égal à 6.
15. Extrayez les influences et les scores de la matrice NIPALS2 afin de créer un nouveau modèle du spectre choisi.
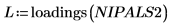
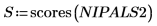
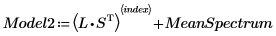
16. Tracez et comparez les deux modèles du spectre choisi. Mettez à l'échelle l'axe horizontal et vertical pour obtenir les valeurs raisonnables.
17. Extrayez la variance cumulée de NIPALS2.
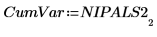
18. Tracez la variance cumulée en fonction du nombre de composants principaux.
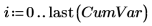
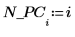
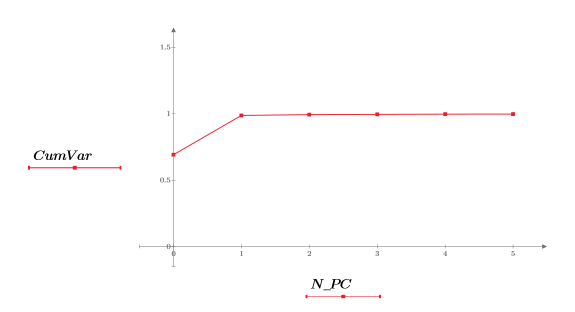
Bien que les deux premiers composants principaux représentent 99 % de la variance, c'est le troisième composant principal qui est déterminant en ce qui concerne le groupement des données par dosage. L'analyse de composant principal réduit les données aux facteurs les plus dominants, mais pas aux facteurs les plus significatifs.