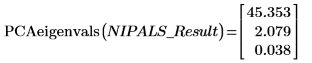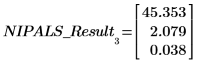Exemple : Analyse de composant principal 1
Utilisez les fonctions Nipals, loadings, scores, PCAeigenvals et PCAvariance pour réaliser une Analyse de composant principal (ACP).
Fonction Nipals
1. Définissez un ensemble de données où chaque colonne représente une variable.


2. Tracez le jeu de données.
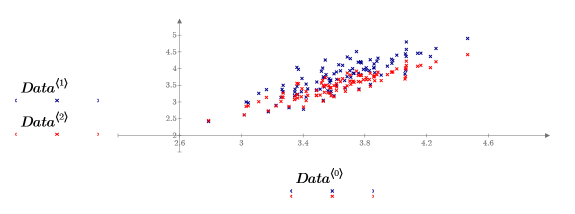
Dans ce graphique, le plan x-y et le plan x-z sont superposés afin d'exposer la tendance dans les données. Les données sont en fait un nuage elliptique de points qui s'étalent quasiment sur un plan. Les trois variables sont liées linéairement et l'écart par rapport à un plan parfait est dû au bruit.
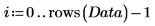
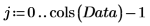
4. Utilisez la fonction de moyenne pour rechercher la moyenne des données et la soustraire de chaque variable afin de centrer les données.
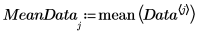
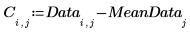
5. Tracez les données centrées.
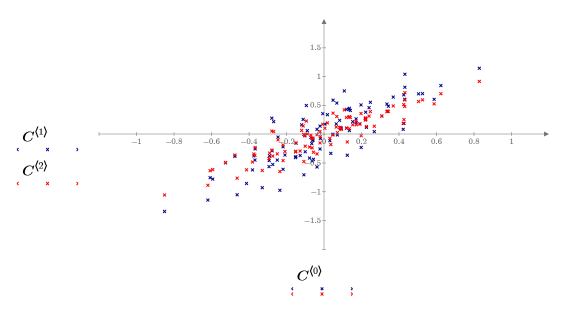
• Les données sont désormais centrées autour de l'origine. Cette opération constitue l'une des étapes que la fonction Nipals exécute automatiquement. • Dans de nombreuses applications d'ACP, il est également souhaitable de mettre les données à l'échelle de façon à ce que les variables possèdent des pondérations égales, comme lorsque différentes variables ont différentes unités. La mise à l'échelle de chaque variable (chaque colonne de Données) en fonction de la variance de l'unité est fréquente. Elle ne convient cependant pas à ces données. Aucune mise à l'échelle n'est donc appliquée ici. |
6. Utilisez la fonction Nipals pour créer un nouvel espace de variable. Utilisez les trois principaux composants, ce qui représente le maximum possible car il n'y a que trois variables avec lesquelles commencer.
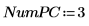
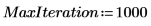
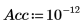
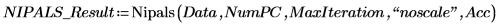
La sortie de la fonction Nipals est une matrice imbriquée de 6 matrices individuelles. Utilisez-la pour rechercher les loadings, les scores, les eigenvals et les eigenvecs des données. Utilisez si nécessaire la fonction Nipals2 et les deux dernières matrices pour extraire des composants supplémentaires.
Loadings et scores
1. Appelez la fonction loadings pour récupérer les données trouvées dans la deuxième matrice de NIPALS_Result.
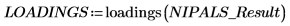
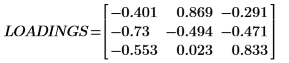
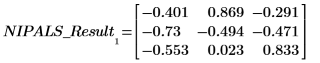
Chaque colonne de LOADINGS est un vecteur de loading.
2. Appelez la fonction scores pour récupérer les données situées dans la première matrice de NIPALS_Result.
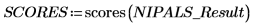

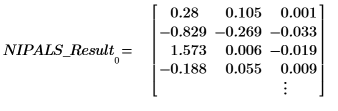
Les scores représentent les proportions dans lesquelles les vecteurs de loading sont ajoutés de façon à recréer le spectre d'origine. Considérez-les comme des intensités. Données = LOADINGS * SCOREST.
3. Tracez les données stockées dans la matrice SCORES.
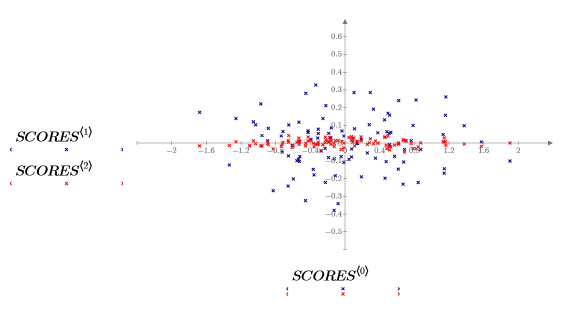
Les données ont été tournées de sorte que le montant maximum de variance puisse être expliqué par la première variable. Ceci est représenté sur le graphique par le long axe de nuage elliptique, qui est désormais parallèle à l'axe x. Les valeurs de la troisième variable, parallèle à l'axe z, sont très faibles. Dans la plupart des cas, cette variable peut être ignorée. Vous avez compressé les données.
Variance d'APC et valeurs propres
1. Utilisez la fonction PCAvariance pour renvoyer les variances cumulées des trois principaux composants.
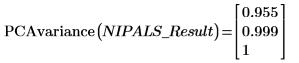
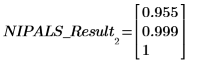
Les deux premiers composants réalisent jusqu'à 99,9 % de la variance dans le système.
2. Utilisez la fonction PCAeigenvals pour extraire les valeurs propres des principaux composants.