Exemple : Régression non linéaire 2
Utilisez la fonction LeastSquaresFit pour effectuer une régression non linéaire. Le solveur LeastSquaresFit offre le plus de flexibilité pour la résolution de problèmes de régression non linéaire. Il vous permet d'entrer des équations de contraintes pour n'importe quel paramètre dépendant, des limites inférieure et supérieure pour les paramètres, des écarts-types sur les valeurs x, ainsi qu'une limite de confiance pour le calcul.
LeastSquaresFit
1. Définissez un jeu de données.
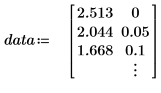
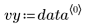
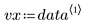
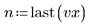
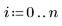
Ces données sont extraites d'un exemple présenté sur le site Web de NIST. Les données ont été générées avec une précision de 14 chiffres à l'aide de l'équation suivante :
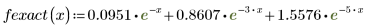
2. Définissez une fonction d'ajustement.
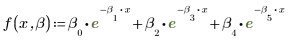
Les paramètres individuels ci-dessus sont des éléments d'un vecteur β. Vous pouvez également spécifier la fonction d'entrée à l'aide de noms de variables individuels, plutôt qu'avec les éléments d'un vecteur :
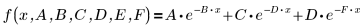
3. Spécifiez des valeurs initiales.
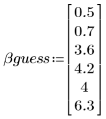
4. Définissez les limites de confiance des paramètres.
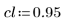
5. Appelez la fonction LeastSquaresFit.
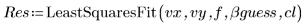
Le solveur utilise l'algorithme SQP pour résoudre le problème de moindres carrés résultant. Avec l'introduction de variables supplémentaires, le problème d'origine se transforme en un problème général de programmation non linéaire avec contraintes, qui est, en général, plus rapide et plus stable que d'autres méthodes.
6. Affichez le vecteur de sortie renvoyé par la fonction LeastSquaresFit.
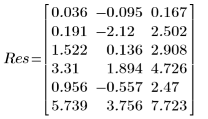
◦ La première colonne de sortie contient les valeurs des paramètres ajustés. La deuxième colonne contient la limite à gauche et la troisième colonne la limite à droite de l'intervalle de confiance des paramètres.
◦ Les limites de confiance de 95 % pour les paramètres couvrent une plage relativement large, montrant que l'ajustement est difficile et que les paramètres individuels peuvent varier fortement. Il en résulte que les valeurs des paramètres ajustés diffèrent des valeurs correctes enregistrées sur le site Web de NIST :
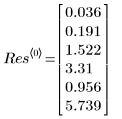

7. Tracez les données, l'ajustement des moindres carrés et l'ajustement NIST.
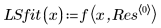
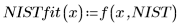
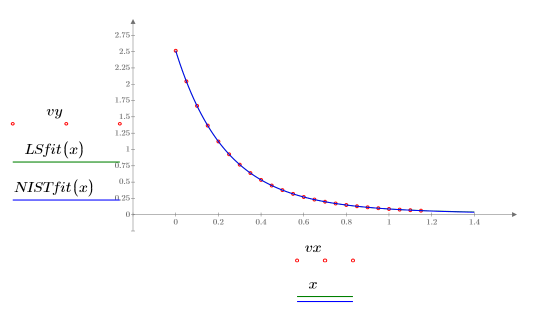
8. Comparez l'ajustement des moindres carrés avec les données d'origine :
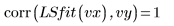
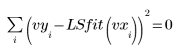
L'ajustement s'approche de la convergence, mais il a pu profiter d'une modification de la tolérance de convergence. Cela peut être réalisé grâce à l'un des arguments en option de la fonction LeastSquaresFit.
Contraintes, écart-type et tolérance
Il existe plusieurs arguments en option pour LeastSquaresFit :
• Vecteur d'écart-type
• Matrice des limites inférieure et supérieure
• Précision
Vous pouvez utiliser n'importe lequel des arguments en option seul, mais si vous entrez plusieurs arguments, l'ordre des arguments a de l'importance.
1. Perturbez l'une des valeurs de données afin de simuler une mesure erronée.
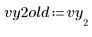
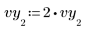
2. Spécifiez les limites inférieure et supérieure des valeurs de l'ajustement.
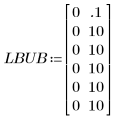
Les limites sont définies bien en-dehors des valeurs attendues des paramètres, car aucune limite particulière n'est connue dans ce cas.
3. Définissez un vecteur d'écarts-types pour chaque valeur y afin de masquer la valeur extrême.
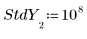
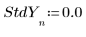
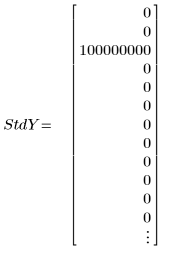
◦ La large valeur de 108 dans l'écart-type supprime en réalité la mesure erronée du calcul.
◦ Lorsqu'un vecteur d'écarts-types est entré en guise d'argument dans la fonction LeastSquaresFit, le solveur minimise la fonction suivante :
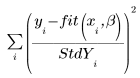
Si l'écart-type est égal à 0 pour un point, la fonction d'origine, sans écart, est alors utilisée sur ce point. Autrement dit, StdYi est configuré sur 1.
4. Définissez la précision de manière à appliquer une tolérance de convergence plus sévère au calcul (la valeur par défaut est égale à 10-7).
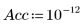
5. Appelez la fonction LeastSquaresFit avec et sans l'écart-type.
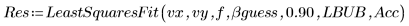
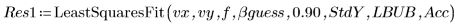
◦ Le calcul non masqué a échoué car les limites de confiance sont trop grandes.
◦ Les nouveaux paramètres sont plus proches des valeurs NIST :
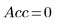
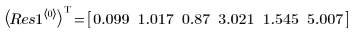
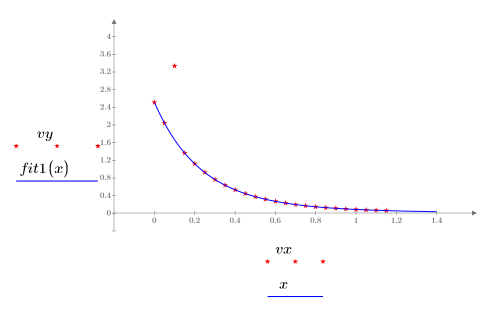
6. Tracez l'ajustement masqué et les données avec la valeur extrême.
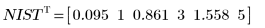
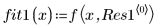
Référence
Les données de cet exemple sont tirées de Lanczos, C., Applied Analysis, Prentice Hall, 1956, pages 272-280, tel que présenté dans le document NIST Statistical Reference Dataset Archive