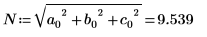Exemple : Fonctions de norme et de déterminant de matrice

Fonctions > Vecteur et matrice > Caractéristiques des tableaux > Exemple : Fonctions de norme et de déterminant de matrice

Exemple : Fonctions de norme et de déterminant de matrice

1. Définissez une matrice carrée.

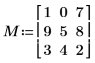
2. Définissez les éléments de matrice en des noms de variables génériques.

Cliquez pour copier cette expression

<region id="ID0ETUVEB" actualWidth="111.93333333333334" actualHeight="69.37360000000001" top="230.40000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="44">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <matrix rows="3" cols="3">
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
        <id labels="VARIABLE" xml:space="preserve">
          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
        </id>
      </matrix>
      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

3. Utilisez la fonction norm1 pour trouver la norme L1 de la matrice M.

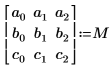
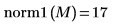
Vous pouvez également trouver la norme L1 en calculant le maximum des sommes de colonnes absolues de M.

<region id="ID0E1XVEB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="403.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0EIYVEB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="441.60000000000008" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="50">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0EWYVEB" actualWidth="156.98000000000002" actualHeight="27.791200000000003" top="480.00000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
  </math>
</region>

<region id="ID0EEZVEB" actualWidth="261.61666666666667" actualHeight="27.791200000000003" top="518.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="54">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">L1</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ACS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

4. Utilisez la fonction norm2 pour trouver la norme L2 de la matrice M.

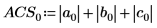
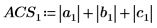
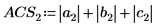
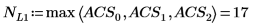
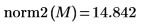
Vous pouvez également utiliser la fonction svds pour trouver la plus grande valeur singulière absolue de la matrice M.

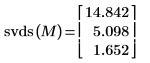
La fonction svds renvoie un vecteur de valeurs singulières triées, de sorte que la valeur placée en haut soit la plus grande valeur singulière de la matrice M.

5. Utilisez la fonction norme pour trouver la norme euclidienne de la matrice M.

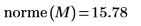
Vous pouvez également calculer manuellement la racine carrée de la somme des carrés absolus de la matrice M.

<region id="ID0EQ6VEB" actualWidth="509.50600031296426" actualHeight="36.780453040075308" top="940.80000000000018" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">e</Subscript></Span>
      </id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <plus />
                <apply>
                  <plus />
                  <apply>
                    <plus />
                    <apply>
                      <plus />
                      <apply>
                        <plus />
                        <apply>
                          <plus />
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                          <apply>
                            <pow />
                            <apply>
                              <absval />
                              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                              </id>
                            </apply>
                            <real>2</real>
                          </apply>
                        </apply>
                        <apply>
                          <pow />
                          <apply>
                            <absval />
                            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                            </id>
                          </apply>
                          <real>2</real>
                        </apply>
                      </apply>
                      <apply>
                        <pow />
                        <apply>
                          <absval />
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                          </id>
                        </apply>
                        <real>2</real>
                      </apply>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <absval />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                          <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                        </id>
                      </apply>
                      <real>2</real>
                    </apply>
                  </apply>
                  <apply>
                    <pow />
                    <apply>
                      <absval />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                      </id>
                    </apply>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <absval />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
              <apply>
                <pow />
                <apply>
                  <absval />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <apply>
                <absval />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                </id>
              </apply>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

6. Utilisez la fonction normi pour trouver la norme infinie de la matrice M.

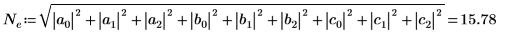
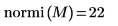
Vous pouvez également utiliser la fonction max pour calculer manuellement le maximum des sommes de lignes absolues de la matrice M.

<region id="ID0EICWEB" actualWidth="158.77333333333334" actualHeight="27.791200000000003" top="1132.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="66">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EWCWEB" actualWidth="156.48333333333335" actualHeight="27.791200000000003" top="1171.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="68">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EEDWEB" actualWidth="155.11333333333334" actualHeight="27.791200000000003" top="1209.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="70">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
      </id>
      <apply>
        <plus />
        <apply>
          <plus />
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
          </apply>
          <apply>
            <absval />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
          </apply>
        </apply>
        <apply>
          <absval />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
          </id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ESDWEB" actualWidth="252.23666666666671" actualHeight="27.791200000000003" top="1248.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="72">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">
        <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">N<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">i</Subscript></Span>
      </id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
            </id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">ARS<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

7. Utilisez la fonction det pour trouver le déterminant de la matrice M.

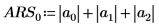
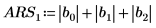
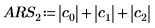
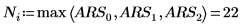
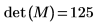
Vous pouvez aussi calculer manuellement le déterminant de la matrice M.

<region id="ID0EKGWEB" actualWidth="490.83" actualHeight="27.791200000000003" top="1401.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="76">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">det</id>
      <eval>
        <apply>
          <plus />
          <apply>
            <minus />
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
            <apply>
              <mult />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
              </id>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                  </apply>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
                    </id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                      <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                    </id>
                  </apply>
                </apply>
              </parens>
            </apply>
          </apply>
          <apply>
            <mult />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
              <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">2</Subscript></Span>
            </id>
            <parens>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                </apply>
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript></Span>
                  </id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                    <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                  </id>
                </apply>
              </apply>
            </parens>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

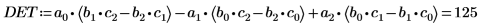
8. Utilisez la fonction norm pour trouver la norme d'un vecteur contenant les éléments de la colonne 0 de la matrice M.

Cliquez pour copier cette expression

<region id="ID0EQIWEB" actualWidth="109.26666666666668" actualHeight="69.37360000000001" top="1497.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="78">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">v</id>
      <eval>
        <matrix rows="3" cols="1">
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
            <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
          </id>
        </matrix>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
  </math>
</region>

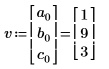
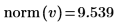
Vous pouvez aussi calculer manuellement la norme du vecteur v.

<region id="ID0EVJWEB" actualWidth="207.04933364629747" actualHeight="36.780453040075308" top="1632.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="82">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">N</id>
      <eval>
        <apply>
          <nthRoot />
          <placeholder />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">a<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
              <apply>
                <pow />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                  <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">b<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
                </id>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <pow />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">c<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript></Span>
              </id>
              <real>2</real>
            </apply>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Rubriques associées

Norme d'une matrice carrée

Est-ce que cela a été utile ?