Exemple : Méthodes de prédiction linéaire
Utilisez les fonctions burg et yulew pour générer les coefficients du modèle de prédiction linéaire. Ces fonctions appliquent la méthode de Burg et l'algorithme de Yule-Walker, respectivement. Pour une description de ces algorithmes et des notions mathématiques qu'ils renferment, voir Sophocles J. Orfanidis, Optimum Signal Processing, Macmillan (1989).
Prédiction de Yule-Walker
1. Utilisez la fonction cos pour définir un signal cosinus.
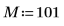
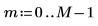
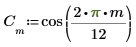
2. Tracez le signal.
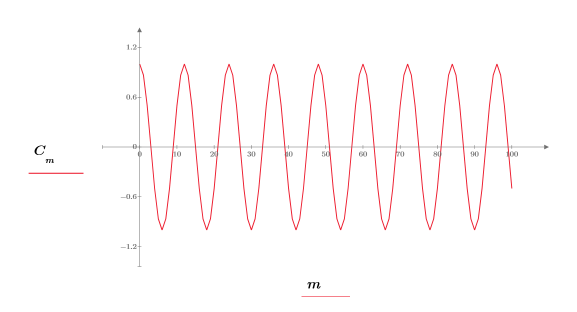
3. Utilisez la fonction rnd pour ajouter du bruit aléatoire au signal.
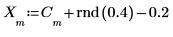
4. Tracez le signal original et le signal parasité.
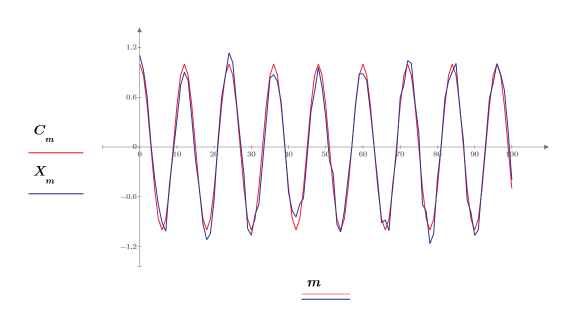
La valeur 0.2 est soustraite du signal afin de centrer la composante aléatoire autour de l'amplitude 0.
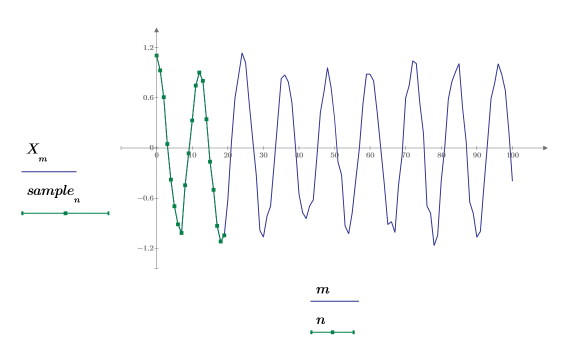
5. Prenez un petit ensemble échantillon au début du signal.
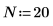
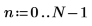
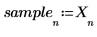
6. Définissez l'ordre de prédiction et utilisez la fonction yulew pour calculer les coefficients.
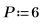
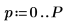

◦ Ces coefficients se réfèrent à un filtre du type "tout pôle", qui est une approximation du signal d'origine. Comme prévu, il y a un grand pôle, représentant le cosinus, et plusieurs petits pôles, approximant le bruit.
◦ L'ordre P détermine le nombre de valeurs consécutives utilisées pour prédire la valeur suivante dans la séquence. Les éléments d'ordre un à six du vecteur des coefficients sont utilisés, en ignorant l'élément d'ordre zéro, qui est toujours égal à 1. Ce 1 est nécessaire lorsque y est utilisé en guise de filtre d'erreur de prédiction pour générer l'ensemble complet des erreurs de prédiction.
7. Comparez les points prédits, calculés à l'aide des P points précédents dans le signal, aux données d'origine. Cela montre à quel point le filtre serait bon s'il était utilisé à la place du signal X.
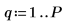
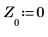
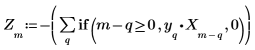
8. Tracez le signal original et le signal prédit.
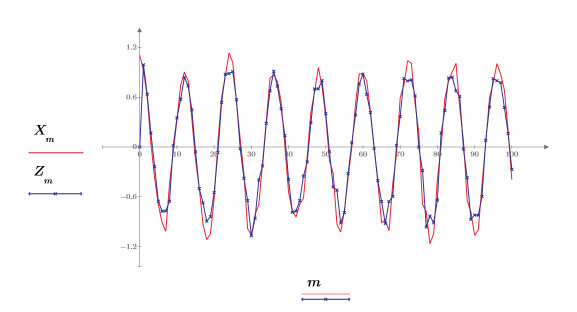
L'approximation est très bonne, même si vous n'utilisez que les 20 premiers points de données.
9. Utilisez la fonction response pour générer les erreurs de prédiction des coefficients de Yule-Walker en utilisant le tableau des coefficients en guise de filtre, puis en calculant la réponse avec l'échantillon en entrée.
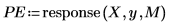
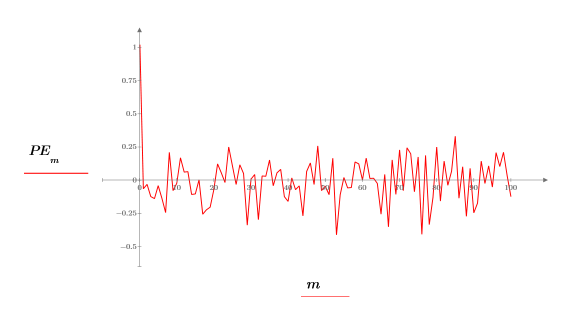
Le tableau complet des coefficients est parfois appelé filtre d'erreur de prédiction.
10. Vérifiez que ces erreurs donnent bien la différence entre les deux tracés précédents.
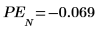
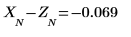
L'algorithme de Yule-Walker minimise la somme des carrés des erreurs de prédiction.
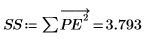
11. Effectuez un contrôle ponctuel de la minimisation en perturbant y (ajoutez pour cela une petite quantité aléatoire à tous les coefficients à l'exception du premier), puis en recalculant la somme (en plaçant le curseur sur la fonction rnd ci-dessous et appuyez plusieurs fois sur [F5]).
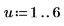
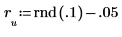
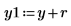
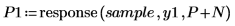
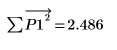
Prédiction de Burg
1. Construisez une séquence pour laquelle la prédiction linéaire doit donner de bons résultats : processus autorégressif à coefficients connus.
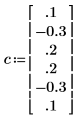
2. Initialisez la série temporelle.
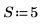
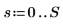
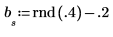
3. Générez le reste de la série à l'aide de l'autorégression et du bruit.
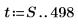
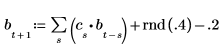
4. Prenez les séries temporelles entières en guise d'échantillon et calculez les coefficients d'un modèle d'ordre 6, puis utilisez la fonction burg pour calculer les coefficients.
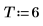
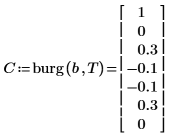
5. Comparez les coefficients qui ont généré le processus en utilisant la convention de signe de ce document.
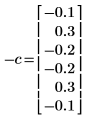
◦ Le coefficient de zéro a été ignoré, car il est toujours égal à 1.
◦ Les éléments calculés 1 et 5 de C sont différents.
6. Utilisez le vecteur des coefficients de Burg C pour générer les erreurs de prédiction.
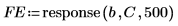
◦ La méthode de Burg attribue un poids égal à 0 à la première erreur P, de telle sorte que la minimisation n'est pas affectée par les zéros de remplissage de l'échantillon, comme c'est le cas pour la minimisation effectuée par la méthode de Yule-Walker.
◦ Le critère de Burg implique également à la fois les erreurs ascendantes FE avant et les erreurs descendantes BE.
7. Utilisez les fonctions response et reverse pour calculer les erreurs descendantes.
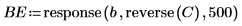
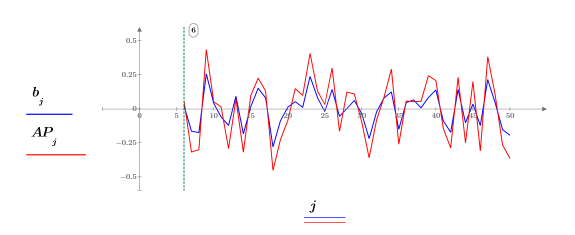
8. Utilisez les erreurs de prédiction FE et la fonction d'autorégression b pour calculer les prédictions réelles AP, puis tracez une partie des séries prédite et réelle en débutant au terme d'ordre Pth.
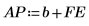
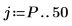
Estimation spectrale
Vous pouvez utiliser les coefficients générés par les méthodes de prédiction linéaire en vue d'estimer le spectre de puissance du processus en cours de modélisation. Dans ce contexte, l'algorithme de Burg est connu sous le nom de méthode MESA (Maximum Entropy Spectrum Analysis ou analyse spectrale par entropie maximum), et dans certains cas il peut déterminer les spectres de séries temporelles courtes de manière plus précise que la FFT.
Estimez le spectre de puissance d'un processus consistant en une somme de sinusoïdes avec du bruit gaussien ajouté.
1. Utilisez la fonction sin pour définir un signal possédant deux composantes sinusoïdales.
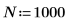
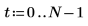
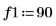
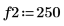
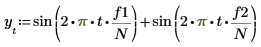
2. Utilisez la fonction gaussn pour ajouter du bruit gaussien.
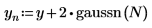
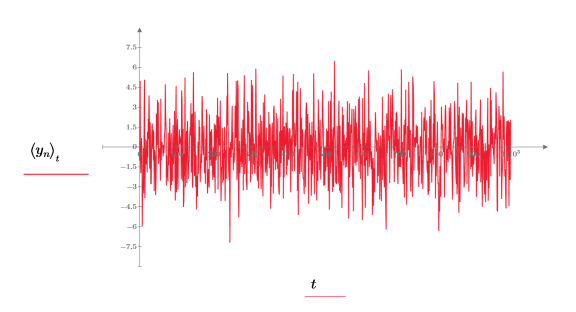
La fonction gaussn renvoie un vecteur de n nombres aléatoires répartis selon une distribution de probabilité gaussienne de moyenne 0 et d'écart-type 1.
3. Définissez deux ordres pour la prédiction linéaire.
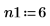
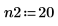
4. Utilisez la fonction burg pour estimer le spectre avec modèles autorégressifs de deux ordres, à l'aide de la série temporelle en guise d'échantillon.
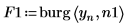
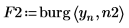
5. Utilisez la fonction gain pour calculer le spectre de puissance correspondant, à savoir le carré de l'amplitude de la fonction de transfert définie par les tableaux de coefficients F1 et F2.
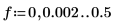
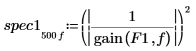
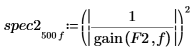
6. Tracez les deux spectres de puissance.
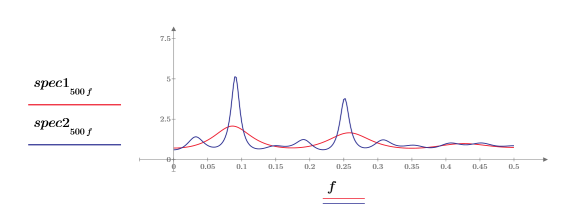
◦ Chaque spectre de puissance comporte deux pics.
◦ Les pics de la fréquence inférieure, ainsi que ceux de la fréquence supérieure, se produisent à environ la même fréquence.
7. Subdivisez les courbes spec1 et spec2 en deux segments chacune, afin de faciliter la recherche de leurs pics de gain et des fréquences auxquelles ils se produisent.
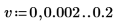 | 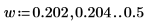 |
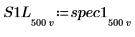 | 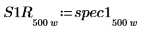 |
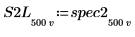 | 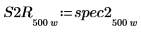 |
8. Utilisez la fonction if pour définir une fonction qui renvoie la fréquence à laquelle le segment donné présente un pic et utilisez-le pour trouver les pics de gauche et droite de chaque courbe de spectre.
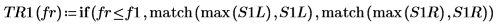 | |
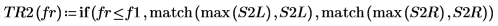 | |
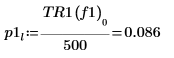 | 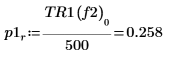 |
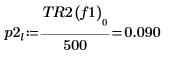 | 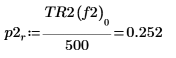 |
9. Utilisez la fonction max pour calculer l'amplitude de chaque pic.
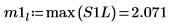 | 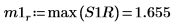 |
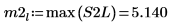 | 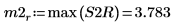 |
10. Tracez chaque fonction séparément. Utilisez des marqueurs horizontaux et verticaux pour montrer l'amplitude de chaque pic et la fréquence à laquelle il se produit.
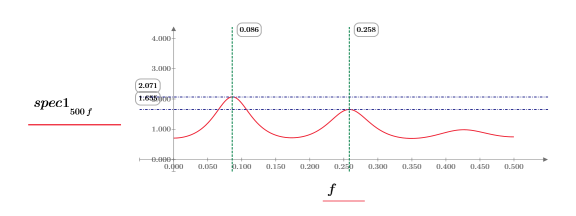
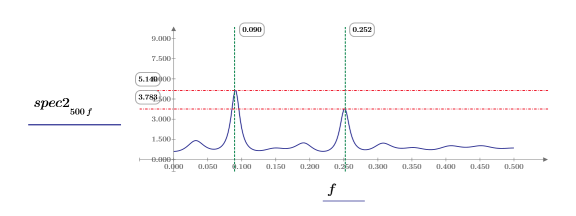
◦ Observez les deux tracés lors du recalcul du document.
◦ L'amplitude des pics varie avec chaque recalcul et ils ont généralement des valeurs différentes. Toutefois, il est possible que les amplitudes soient égales.
◦ Les pics surviennent à environ la même fréquence.
Pour plus d'informations sur cette méthode d'estimation spectrale, voir Digital Spectral Analysis with Applications par S. Lawrence Marple, Jr. (Prentice-Hall, Inc.).