Exemple : Interpolation et échantillonnage
Utilisez les fonctions multirate, resample et upsample pour modifier le taux d'échantillonnage d'un signal de différentes manières et sous différentes hypothèses.
Fonction multirate avec filtre FIR par défaut
La fonction multirate utilise le délai de groupe d'un filtre FIR de phase linéaire FIR pour estimer où se termine le transitoire de sortie initiale, et tronque la partie du signal de sortie qui contient le transitoire.
1. Définissez les paramètres du signal.
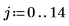 |
|
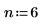 |
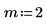 |
2. Utilisez la fonction sin pour définir un signal de sommes de sinus.
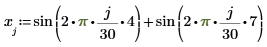
3. Appliquez la fonction multirate au signal.
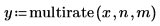
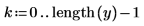
4. Tracez le signal rééchantillonné.
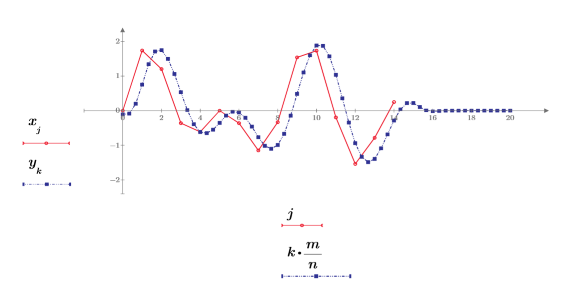
Le tracé montre que le signal rééchantillonné est légèrement décalé et qu'il contient n/m fois le nombre de points de données d'origine. Le décalage est introduit par le filtre FIR et est égal à son délai de groupe.
Fonction multirate avec filtre FIR passe-bas en option
1. Définissez la fréquence de coupure, le nombre de coefficients et le type de fenêtre surélevée.
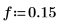 | 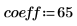 | 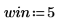 |
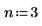 | 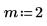 |
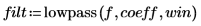
3. Utilisez la fonction multirate pour rééchantillonner le signal x avec un autre facteur.
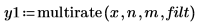
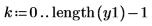
4. Tracez le signal rééchantillonné.
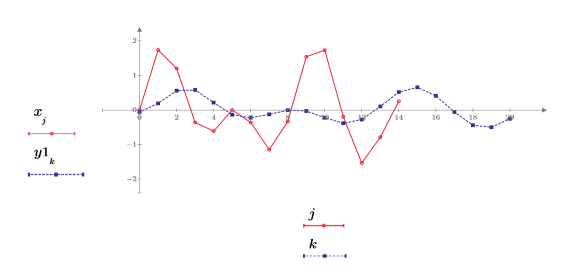
Le rééchantillonnage produit une atténuation du signal, car le filtre FIR n'a pas un gain égal au taux de suréchantillonnage n.
5. Ajustez les coefficients du filtre FIR sur le gain correct et retracez le signal rééchantillonné.
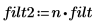
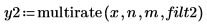
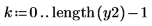
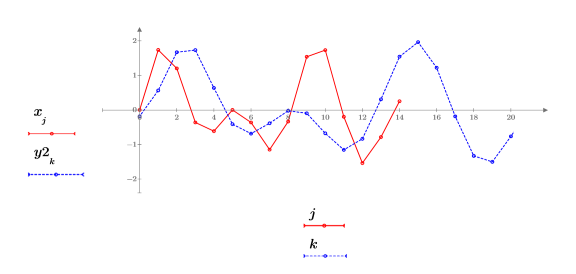
L'ajustement des coefficients du filtre FIR a supprimé l'effet de mise à l'échelle.
Suréchantillonnage des signaux
Vous pouvez utiliser la fonction multirate pour suréchantillonner ou sous-échantillonner un signal.
1. Utilisez la fonction multirate pour suréchantillonner le signal x en augmentant le rapport n/m.
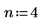 | 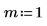 |
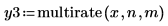 | |
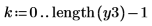 |
2. Tracez le signal suréchantillonné.
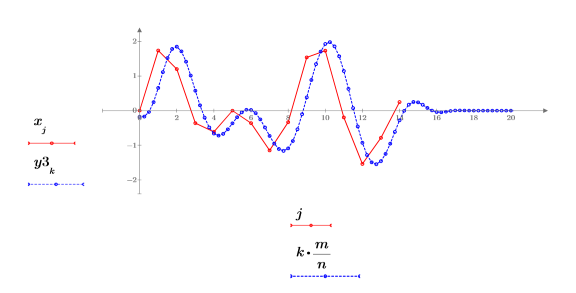
L'augmentation du rapport n/m entraîne celle du nombre d'échantillons totaux (comme l'indique la valeur de la longueur), ainsi que celle du nombre de nouveaux échantillons entre deux échantillons consécutifs quelconques du signal d'origine.
3. Utilisez la fonction multirate pour sous-échantillonner le signal x en diminuant le rapport n/m.
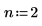 | 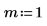 |
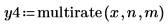 | |
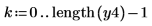 |
4. Tracez le signal sous-échantillonné.
La diminution du rapport n/m entraîne celle du nombre d'échantillons totaux (comme l'indique la valeur de la longueur), ainsi que celle du nombre de nouveaux échantillons entre deux échantillons consécutifs quelconques du signal d'origine.
Suréchantillonnage des données
La fonction upsample effectue une FFT sur les données d'origine, en ajoutant des zéros au milieu de la plage de coefficients en vue de créer une transformée possédant la longueur interpolée requise, puis en effectuant la transformée inverse du spectre étendu. Il n'y a pas de méthode unique pour l'interpolation des données. Il est également possible d'utiliser un filtre FIR spécifiquement conçu. Cette fonction renvoie une interpolation raisonnable pour les données qui se comportent de manière régulière.
1. Définissez le facteur d'interpolation n et appliquez la fonction upsample au signal x.
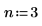
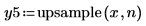
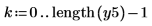
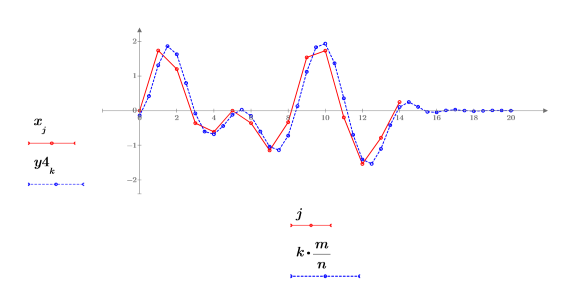
2. Tracez le signal renvoyé.
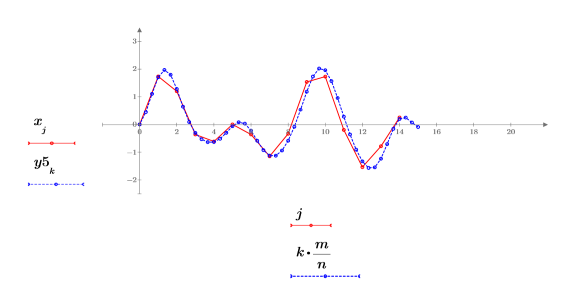
Le signal renvoyé y est une version interpolée du signal x avec n fois le nombre de points.
Rééchantillonnage du signal
La fonction resample utilise l'interpolation, comme ci-dessus, en produisant n fois le nombre de points, puis en prenant chaque point d'ordre mth pour générer la sortie.
1. Définissez le facteur de décimation m et le facteur d'interpolation n.
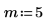 | 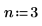 |
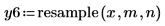 | |
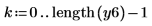 |
2. Tracez le signal renvoyé.
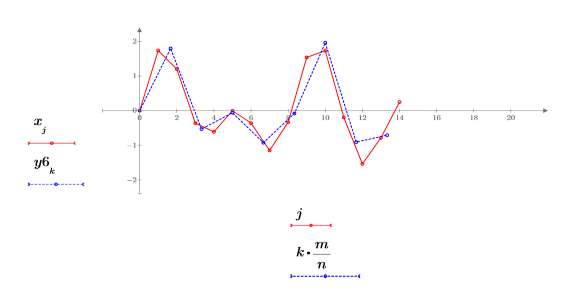
Le signal renvoyé comporte 3/5 points, de telle sorte que l'espacement entre les échantillons est égal à l'espacement d'origine 5/3.
Utilisation du suréchantillonnage à l'aide d'entrées non périodiques et périodiques
La fonction upsample suppose que l'entrée est périodique. Examinez le signal renvoyé dans les deux cas.
Entrée non périodique
1. Définissez le facteur d'interpolation.
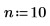
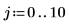
2. Définissez un signal d'entrée non périodique.
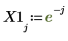
3. Appliquez la fonction upsample.
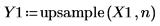
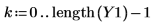
4. Tracez le signal renvoyé.
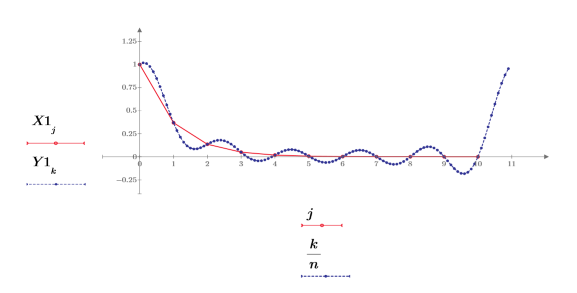
La routine d'interpolation suppose que X est périodique. Par conséquent, elle essaie d'interpoler les points à proximité de la fin du graphe, qui reviendra à la hauteur initiale de 1. Toutefois, la fonction donne des résultats tangibles si l'"emballage" de la séquence d'entrée donne une fonction relativement lisse.
Entrée périodique
1. Définissez le facteur d'interpolation.
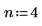
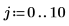
2. Définissez un signal d'entrée périodique.
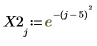
3. Appliquez la fonction upsample.
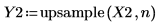
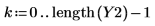
4. Tracez le signal renvoyé.
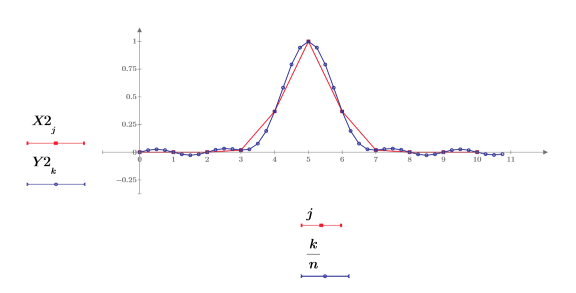
L'interpolation est une approximation plus proche du signal d'origine lorsque ce signal est périodique.