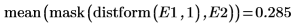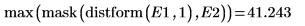Exemple : Transformée de distance euclidienne
Utilisez la fonction M pour calculer la transformée de distance euclidienne de la matrice distform, en considérant les pixels de valeur fg comme étant des pixels d'avant-plan.
Pour plus d'informations sur l'utilisation de cet exemple, voir A propos des exemples de traitement d'image.
Matrice d'image
1. Définissez une matrice d'image et appliquez-lui distform.
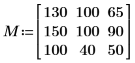
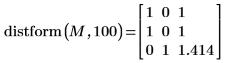
La valeur de chaque pixel de sortie est la distance au pixel d'avant-plan d'entrée le plus proche (valeur 100) :
◦ La distance de sortie est égale à zéro pour les pixels d'avant-plan d'entrée
◦ La distance est égale à 1 pour les voisins horizontaux et verticaux
◦ Pour les voisins diagonaux, la distance est la racine carrée de 2 ou 1.414
Image avec un pixel unique non égal à zéro
1. Définissez une image avec un pixel unique, différent de zéro.
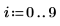
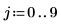
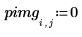
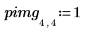

2. Appliquez distform à l'image :
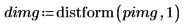
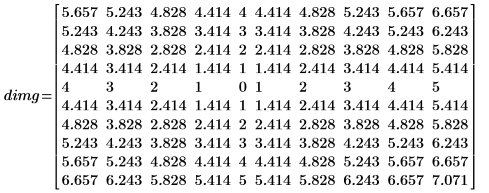
La distance augmente de manière monotone lorsqu'on s'écarte du pixel d'avant-plan (pixel central) dans l'image d'entrée.
La transformée de distance produit une distance euclidienne approximative. Dans l'exemple ci-dessus, vous pouvez voir que la sortie exacte de la transformée de distance euclidienne pour l'emplacement de matrice (0,1) doit être :
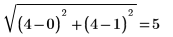
tandis que, dans notre image de sortie, la valeur est 5.243.
Image d'un objet circulaire
1. Définissez une image d'un cercle :
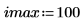
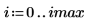
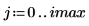
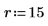
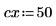
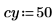
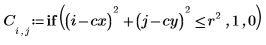
2. Utilisez la fonction scale pour mettre le cercle à l'échelle.
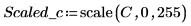
3. Utilisez la fonction WRITEBMP pour écrire le cercle mis à l'échelle dans un fichier.
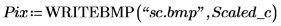
4. Appliquez la fonction distform au cercle, mettez-le à l'échelle et enregistrez les résultats dans un nouveau fichier.
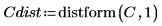
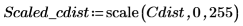
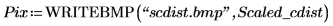
5. Insérez les images à partir des deux fichiers et comparez le résultat.
(sc.bmp) | (scdist.bmp) |
Les valeurs des distances sont égales à zéro pour tous les points situés à l'intérieur du cercle et elles augmentent de manière monotone lorsqu'on se déplace vers l'extérieur, mais elles ne sont pas exactement égales à la distance euclidienne, sinon la sortie serait radialement symétrique.
Deux images binaires d'un même objet
1. Lisez dans une image.
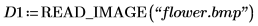
2. Utilisez la fonction translate pour créer des versions translatées de l'image, puis écrivez les images translatées dans des fichiers.
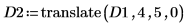
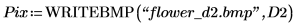
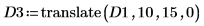
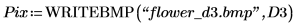
3. Insérez les images à partir des trois fichiers et comparez le résultat.
(flower.bmp) | (flower_d2.bmp) | (flower_d3.bmp) |
4. Utilisez la fonction distform pour calculer la transformée de distance de D1.
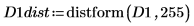
5. Utilisez les fonctions mask et mean pour masquer l'image de la transformée de distance avec les images D2 et D3, puis calculez la moyenne de l'image entière. Cela représente une mesure de la distance entre les deux images.
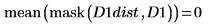
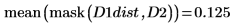
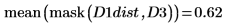
La distance entre D1 et D1 est égale à zéro, et la distance entre D1 et les autres images augmente avec le degré de translation.
6. Calcul de la distance de Hausdorff
La distance de Hausdorff est définie comme la valeur maximale de la distance minimale entre les points de deux ensembles. Pour calculer la distance de Hausdorff entre les deux images, utilisez la fonction max au lieu de la fonction mean.
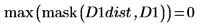
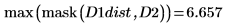
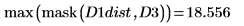
Deux images de contours
Vous pouvez comparer les performances des détecteurs de contours en calculant la distance entre les images de contours. Utilisez la valeur moyenne ou la valeur maximale des distances masquées en guise de mesure de la distance entre les contours.
1. Utilisez la fonction READ_IMAGE pour lire un fichier image.
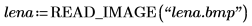
2. Appliquez les deux détecteurs d'arêtes canny et binarize à l'image, puis écrivez les résultats dans les fichiers externes.
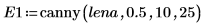
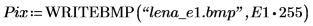
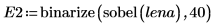
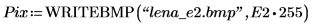
3. Insérez les deux images, puis comparez-les visuellement.
(lena_e1.bmp) | (lena_e2.bmp) |
4. Calculez la distance globale entre les arêtes.