Exemple : Facteurs de suppression de distorsion
Utilisez les fonctions fractfact, fractresol, fractruns, fractalias, quickscreen, effectsgraph, foldover et stack pour analyser les différents facteurs d'une expérience qui étudie le temps requis par l'œil pour effectuer la mise au point d'une image. Les facteurs choisis pour l'expérience sont les suivants :
|
A :
|
Acuité de la vision
|
|
B :
|
Distance entre la cible et l'oeil
|
|
C :
|
Forme cible
|
|
D :
|
Niveau d'éclairage
|
|
E :
|
Taille de la cible
|
|
F :
|
Densité
|
|
G :
|
Objet
|
On suppose que seuls quelques facteurs sont importants et que les interactions d'ordre supérieur entre les différents facteurs peuvent être négligées.
1. Définissez le nombre de facteurs de l'expérience.
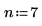
2. Définissez la puissance fractionnaire d'un plan factoriel fractionnaire.
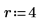
3. Appelez fractfact pour créer la matrice d'expériences X.
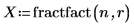
4. Définissez la chaîne gen pour enregistrer les facteurs et la distorsion de la matrice d'expériences X.
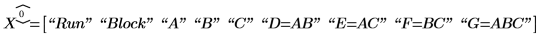
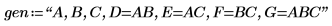
5. Appelez fractresol et fractruns pour déterminer la résolution et le nombre d'exécutions de la matrice d'expériences X.
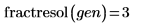
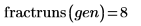
La matrice d'expériences X représente un plan factoriel fractionnaire à 8 exécutions et de résolution III (ses facteurs principaux ne sont pas aliasés l'un avec l'autre, mais ils sont aliasés avec les interactions du second ordre).
6. Enregistrez les résultats de l'expérience dans la matrice Y1 avec une ligne par exécution et une colonne par réplique.

7. Appelez la fonction quickscreen.

8. Appelez la fonction effectsgraph et créez un tracé des effets afin de déterminer quels facteurs sont significatifs.
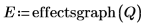

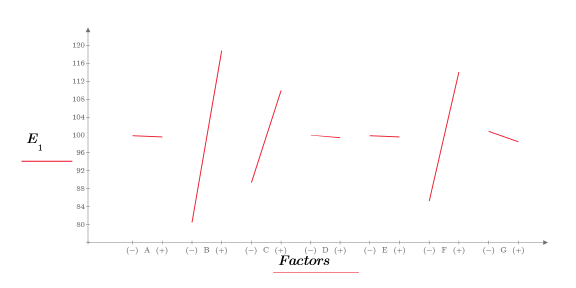
Les facteurs B, C et F affichent des effets importants.
9. Appelez fractalias afin de déterminer quelles interactions du second ordre sont aliasées avec B, C et F.
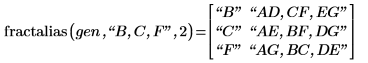
Si B et C sont des facteurs significatifs, il est fort probable que l'interaction BC soit également significative. BC est aliasé avec F et l'on ne sait pas si l'effet observé pour F est causé par F ou BC. Le même problème se produit pour B et F, et pour C et F. Les facteurs principaux et les interactions du second ordre doivent être désaliasés.
10. Appelez foldover pour replier la matrice d'expériences X et pour casser les alias entre les facteurs principaux et les interactions du second ordre.
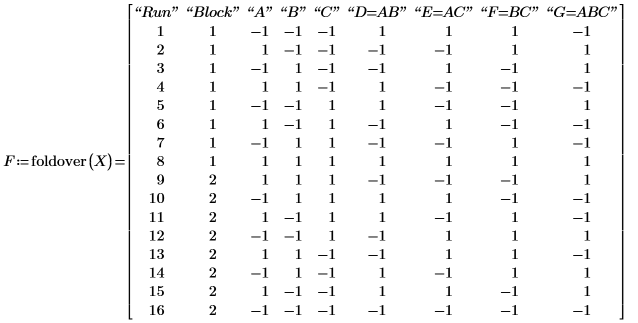
Les huit lignes de la matrice X sont inversées dans la moitié inférieure de F. Vous pouvez spécifier les facteurs à replier.
11. Enregistrez les résultats des exécutions supplémentaires de la matrice d'expériences repliée F.

12. Utilisez la fonction stack pour empiler l'exécution d'origine et les exécutions supplémentaires dans la matrice Y.
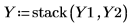
13. Appelez les fonctions quickscreen et effectsgraph et créez un tracé des effets afin de déterminer les effets des facteurs.

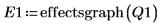
Seuls les facteurs B et F sont significatifs. L'effet précédent constaté pour le facteur C était par conséquent dû à l'interaction BF. Vous pouvez maintenant réaliser des expériences supplémentaires pour analyser comment le facteur B (la distance entre la cible et l'oeil) et le facteur F (la densité) influencent le temps de mise au point.
Référence
Montgomery, D.C., Design and Analysis of Experiments, 5th ed, John Wiley & Sons, New York, 2001, pp. 341.