Exemple : Cepstre et cepstre complexe
Utilisez les fonctions cepstrum et ccepstrum pour calculer le cepstre et le cepstre complexe d'un signal multicanal, à valeurs réelles.
Le cepstre établit une correspondance entre convolution et déconvolution et l'addition et la soustraction dans le domaine des fréquences, et possède des applications dans le traitement de la parole et des signaux géophysiques.
cepstre
Le cepstre d'une séquence x(n) est obtenu grâce à la formule suivante :
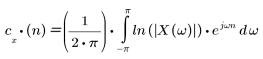
où X (ω) est la transformée de Fourier de la séquence x(n).
Il s'agit de la définition de la transformée inverse après l'application d'un algorithme naturel à la transformée de Fourier de x(n). Le logarithme établit une correspondance entre la convolution dans le domaine temporel et l'addition dans le domaine de la fréquence, faisant du cepstre l'outil idéal pour la déconvolution du signal, qui est mis en correspondance avec la soustraction.
1. Définissez la plage de n.
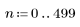
2. Définissez la fonction de séquence x.
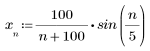
3. Tracez la fonction de séquence x.
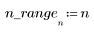
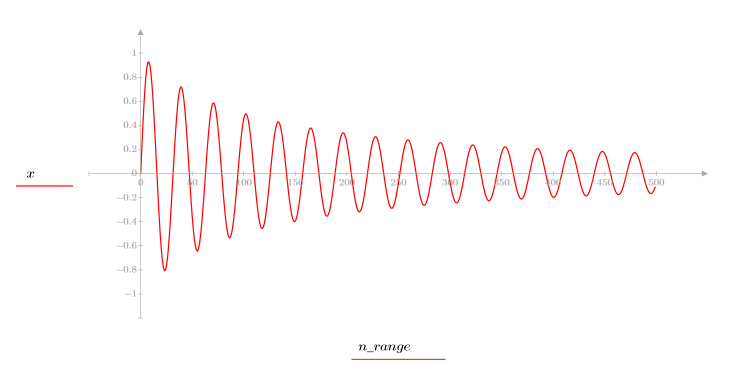
4. Calculez le cepstre et tracez la fonction obtenue.
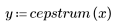
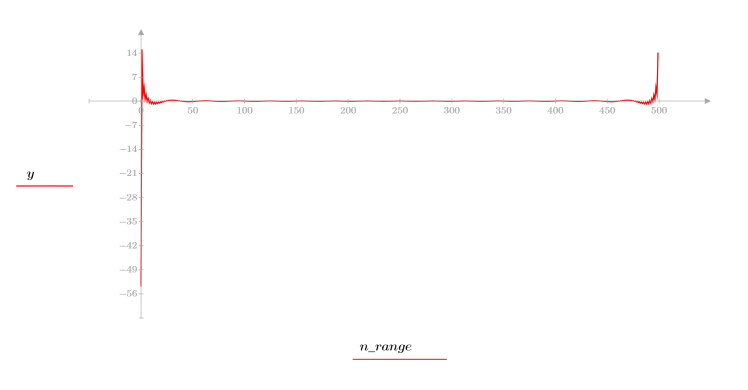
5. Utilisez la fonction recenter pour recentrer le résultat pour amener le premier élément au milieu.
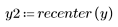
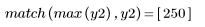
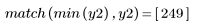
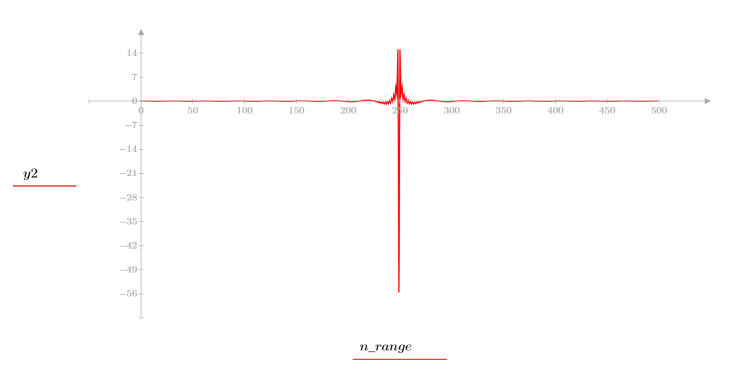
Le signal d'origine ne peut pas être récupéré à partir du cepstre car l'information de phase n'est pas retenue.
ccepstrum
La fonction de cepstre complexe est obtenue grâce au logarithme complexe suivant.
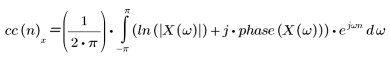
où : X(ω) est la transformée Fourier de la séquence x(n), et la phase sert à capturer l'information de phase de la séquence donnée.
La comparaison entre le cepstre complexe du signal de sortie et celui des séquences d'entrée et du canal montre que le cepstre complexe de la sortie correspond à la somme du cepstre complexe de l'entrée et du canal. On peut comparer cela à l'ajout du spectre de deux signaux dans le domaine de fréquences, mais réalisé dans le domaine temporel.
L'exemple suivant simule un signal passant par un canal de communication produisant un écho (section 12.8.1 de Oppenheim and Schaefer, Prentice-Hall, 1989).
1. Définissez et tracez la réponse du canal sous forme de filtre FIR qui introduit des copies atténuées d'une autre séquence (écho).
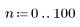
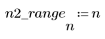
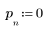
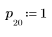
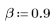
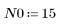
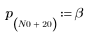
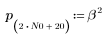
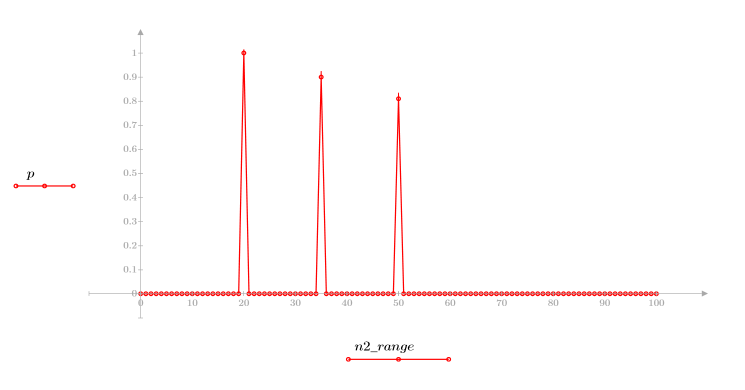
2. Définissez et tracez la séquence v qui sera associée à la réponse du canal.
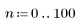
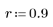
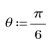
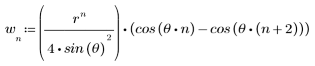
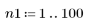
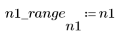
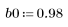
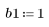

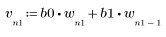
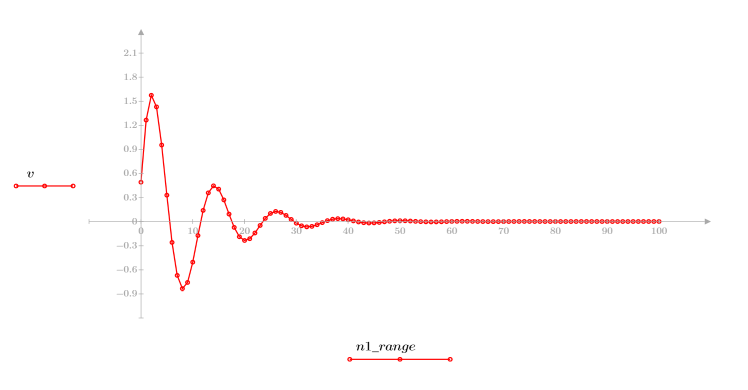
3. Utilisez la fonction response pour obtenir la réponse vectorielle de terme n du vecteur d'entrée p au filtre FIR avec le tableau de coefficient v (la fonction v du canal de communication).
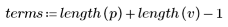
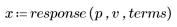
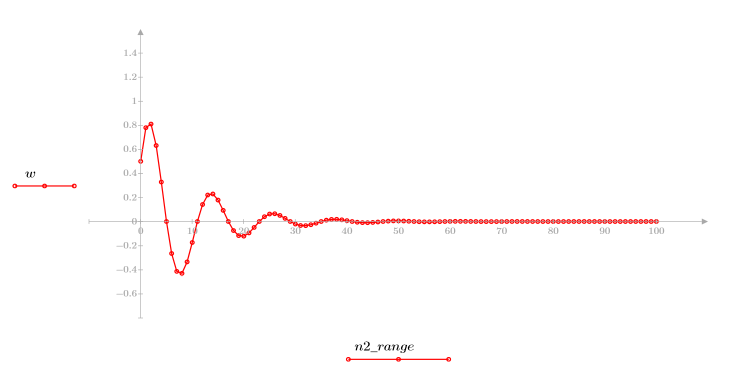
4. Tracez la fonction de réponse.
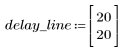
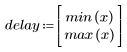
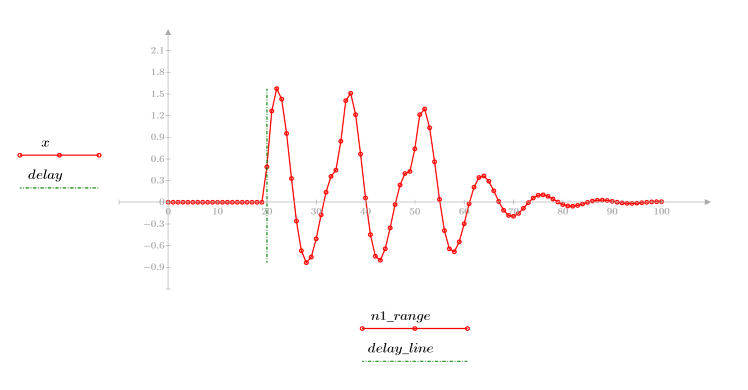
◦ La séquence résultante correspond à la convolution de la fonction d'entrée p et de la fonction du canal de communication v.
◦ La séquence indique le signal d'origine plus les répliques retardées.
5. Comparez le cepstre complexe du signal de sortie avec les cepstres des séquences d'origine. Recentrez les résultats pour faciliter la comparaison.
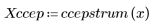
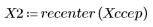
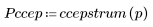
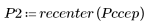
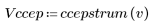
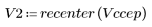
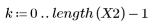
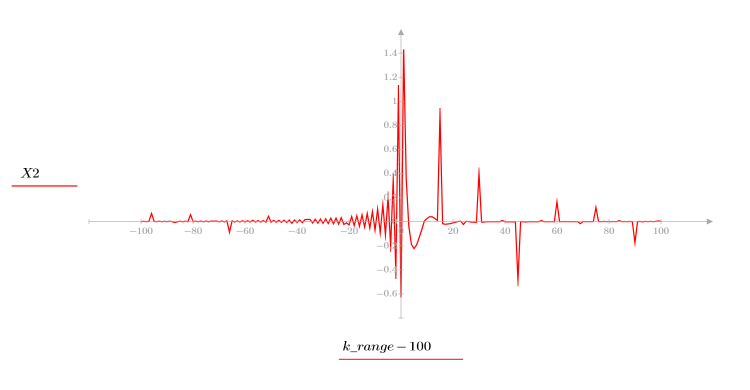
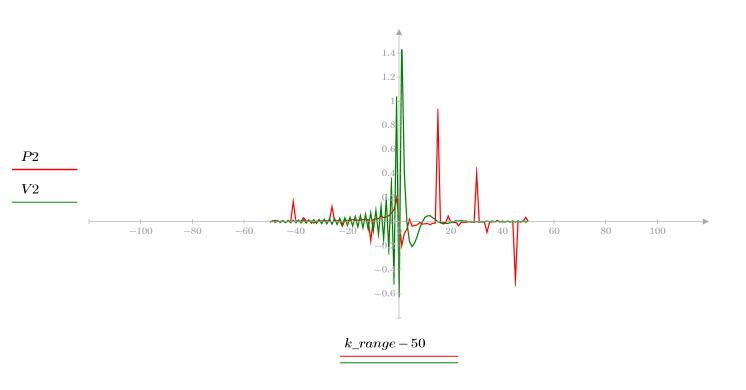
Les tracés ci-dessus montrent que le cepstre complexe du signal de sortie correspond à la somme du cepstre complexe de deux séquences associées en convolution l'une avec l'autre.