A propos des valeurs initiales
Des valeurs initiales sont requises pour toutes les variables inconnues lors de la résolution d'équations linéaires et non linéaires ou de l'optimisation d'une fonction :
• En cas de systèmes linéaires, les valeurs initiales ne servent qu'à déterminer la taille du résultat ; leurs valeurs importent peu.
Les blocs de résolution ci-dessous montrent comment les différentes valeurs initiales de x n'ont aucun effet sur le résultat de la solution renvoyée :
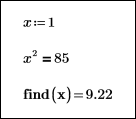 |
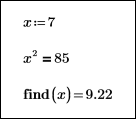 |
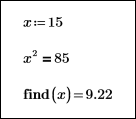 |
• En présence de problèmes non linéaires, la solution dépend considérablement des valeurs initiales. Les remarques portant sur le choix et la modification des valeurs initiales pour la fonction root s'appliquent également ici.
Définition des valeurs initiales
Pour find et minerr, vous devez définir les valeurs inconnues lorsque vous appelez la fonction de bloc de résolution. Les valeurs initiales doivent porter le même nom que les variables inconnues.
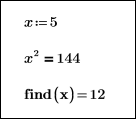
Pour minimize et maximize, les variables inconnues sont faciles à identifier puisqu'elles sont les arguments de la fonction objective (la fonction à optimiser). Toutefois, vous devez définir une valeur initiale pour chacune des variables inconnues de la fonction de bloc de résolution. Lors de la transmission à minimize des valeurs initiales, vous devez conserver l'ordre des arguments de la fonction objective. Ici, a est la valeur initiale de θ et b celle de φ :

Valeurs initiales réelles ou complexes
Les blocs de résolution commencent par évaluer les contraintes au niveau des valeurs initiales pour rechercher les erreurs et déterminer le domaine des solutions.
Si les valeurs initiales sont réelles et que l'évaluation des côtés gauche et droite des contraintes aux valeurs initiales produit uniquement des valeurs réelles ou des matrices de valeurs réelles, une véritable solution est nécessaire. Dans le cas contraire, le solveur peut renvoyer une solution complexe.