Ejemplo: solver de espacio de estado
Utilice el solver statespace para resolver una representación espacial del estado de un sistema de ecuaciones diferenciales ordinarias (ODE) de primer orden.
Específicamente, busque la solución para el caso de oscilador armónico sin forzar en que el lado derecho de la ecuación de oscilación armónica es 0:
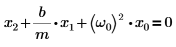
Existen tres casos para la solución: sobreamortiguada, con amortiguación crítica y subamortiguada. |
Solución sobreamortiguada
1. Escriba la ecuación matemática de la solución sobreamortiguada:
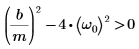
2. Defina las condiciones iniciales, la masa del objeto, la constante de amortiguación, el inicio y el fin del intervalo de integración, y el número de puntos:
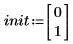
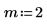
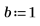
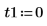
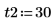
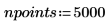
3. Defina la frecuencia natural, o resonante, del sistema.
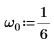
4. Verifique que la condiciones de sobreamortiguación existe:
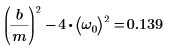
5. Escriba la EDO en la forma matricial:
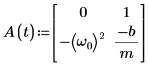
6. Llame a la función statespace:
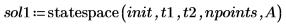
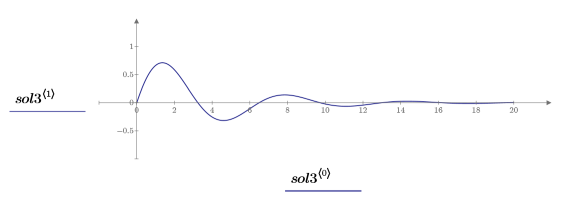
7. Trace la solución:
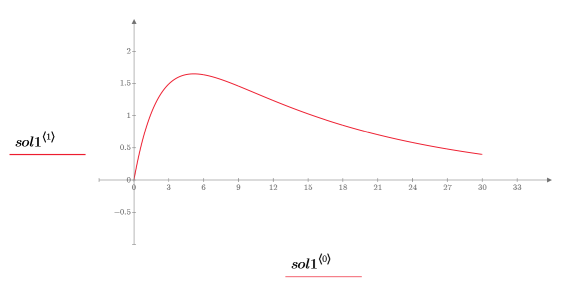
Solución con amortiguación crítica
1. Defina la frecuencia natural, o resonante, del sistema.
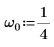
2. Verifique que la condiciones de amortiguación crítica existe:
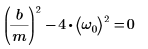
3. Escriba la EDO en la forma matricial:
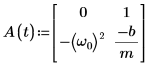
4. Llame a la función statespace:
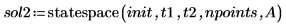
5. Trace la solución:
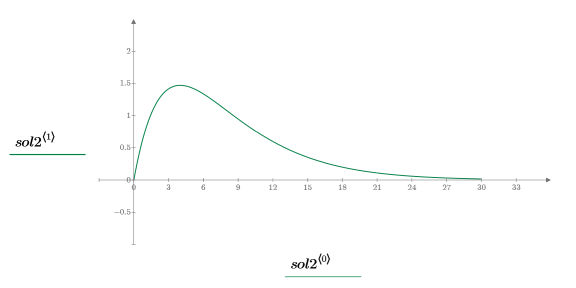
Solución subamortiguada
1. Defina la frecuencia natural, o resonante, del sistema.
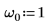
2. Verifique que la condiciones de subamortiguación existe:
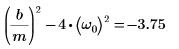
3. Escriba la EDO en la forma matricial:
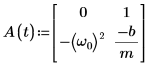
4. Llame a la función statespace:
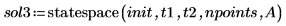
5. Trace la solución: