Ejemplo: análisis de retención del predictor de regresión múltiple
Utilice funciones y programas de DOE para encontrar regresiones estadísticamente significativas. Utilice la aproximación de fuerza bruta donde se prueben todas las combinaciones de factores. Se trata de una tarea difícil reservada para aplicaciones estadísticas avanzadas. En PTC Mathcad, se pueden usar funciones recurrentes para garantizar que se incluyan todas las combinaciones al mismo tiempo que se minimiza la longitud de los programas.
1. Defina un conjunto de datos experimentales.

2. Extraiga el número de factores de Data.
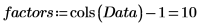
El número de regresiones potenciales de este experimento es el siguiente:
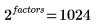
3. Extraiga la fila de cabecera.
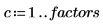
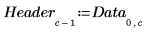
4. Extraiga las frecuencias de errores (Y) y los factores potenciales (X).
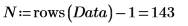
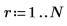
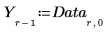
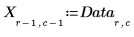
5. Utilice las funciones rows y concat para crear un programa de búsqueda de términos para usarlos al probar regresiones.

Por ejemplo, para los factores "A", "B" y "C", los términos son:
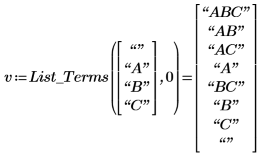
◦ El primer argumento de List_Terms es un vector que comienza con una cadena vacía que se debe tener en cuenta para la constante de regresión, seguido de los nombres de todos los factores.
◦ El segundo argumento debe comenzar en 0. Lo utilizan los bucles del programa de forma recurrente hasta que se alcanza el resultado deseado.
◦ Los términos devueltos son una selección de todas las posibles combinaciones de factores. Por ejemplo, CBA o ACB se omiten ya que su uso en las regresiones produciría el mismo resultado que ABC.
6. Utilice las funciones rows y vec2str para crear un programa para asignar términos a caracteres únicos. La lista devuelta se usa como referencia para que los términos se puedan recuperar más tarde.

La primera columna de la lista devuelta contiene caracteres y la segunda, los términos correspondientes.
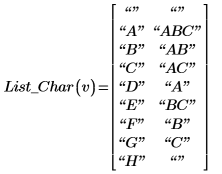
7. Utilice las funciones rows, strlen, match y substr para crear programas para reducir los términos y los datos experimentales.


8. Cree un programa para determinar si la regresión que ha generado la función polyfitstat cumple sus requisitos, tanto en términos de significancia (P) como en el modo en que la regresión describe los datos (R2).

9. Cree un programa para formatear los resultados de la regresión. El programa devuelve los nombres de los términos originales así como R2 y P para continuar con la clasificación cuando se identifiquen todas las regresiones.

10. Cree un programa para ordenar los resultados por la importancia de regresión global (P).
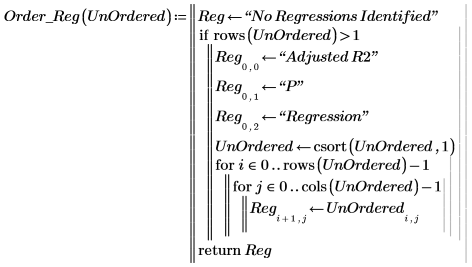
11. Utilice la función polyfitstat para crear un programa para procesar el análisis de regresión. Este breve, pero potente, programa realiza las siguientes tareas:
◦ Buscar todas las combinaciones de predictores.
◦ Itera por todas las combinaciones de predictores y crea una regresión para cada combinación.
◦ Prueba si las regresiones satisfacen los requisitos indicados.
◦ Formatea las regresiones válidas.
◦ Ordena las regresiones formateadas.

12. Llama al programa Reg para procesar el análisis de regresiones.
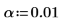
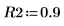
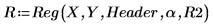
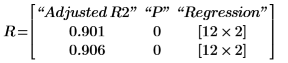
Este programa puede requerir una cantidad de tiempo importante para devolver un resultado, en especial si el número de regresiones aumenta (por ejemplo, si aumenta el nivel de significancia). En este caso, el programa devuelve dos regresiones que satisfacen los requisitos definidos por α y R2.
13. Vea algunos de los resultados del análisis de regresiones.
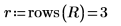

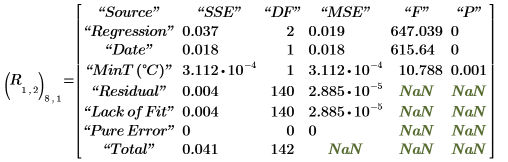


14. Defina f como la ecuación de regresión estándar.
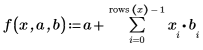
15. Redefina f de modo que tome los coeficientes de regresión devueltos por Reg.
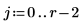
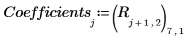
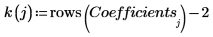
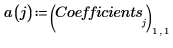
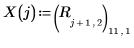
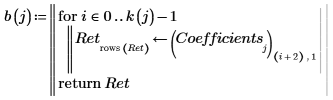
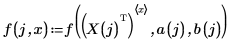
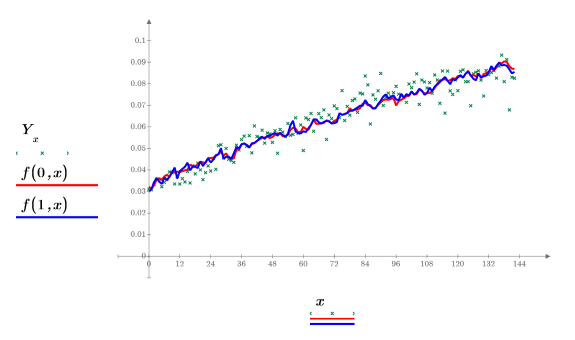
16. Trace los datos experimentales y las regresiones.
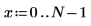
Referencia
Philip Leitch, BSc (Applied Biology/Environmental Science Hons), MBA (Hons)