Ejemplo: regresión lineal
Utilice las funciones polyfitc, line, slope e intercept para buscar la línea de mínimos cuadrados de trayectoria de ajuste en un conjunto de datos x-y. Utilice la función stderr para calcular el error de los parámetros ajustados. Calcule los límites de confianza alrededor de la línea de trayectoria de ajuste y cree intervalos de confianza.
Línea de trayectoria de ajuste
Cree una función lineal para realizar un cálculo aproximado del tiempo necesario para recorrer distintas distancias.
1. Defina un conjunto de distancias en millas y el tiempo que se tarda, en minutos, en recorrer dichas distancias.
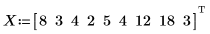
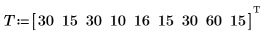
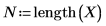
2. Defina una ecuación de regresión lineal univariada.
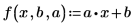
3. Llame a polyfitc para calcular los coeficientes de regresión a y b.
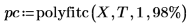
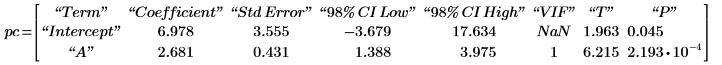
Los coeficientes son tales que la diferencia entre los valores de T y los valores calculados por la ecuación de regresión f es mínima para cada valor x. Para verificarlo, use un bloque de resolución y la función minimize para minimizar la suma de cuadrados:

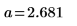
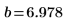
4. Defina la línea de trayectoria de ajuste que minimiza la suma de los cuadrados de las distancias desde cada punto hasta la línea.
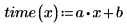
Solo debe utilizar la ecuación parametrizada de la regresión lineal o de cualquier otro tipo para los valores que se acerquen a los datos originales observados. La línea de trayectoria de ajuste para los datos anteriores predice que se tarda el tiempo siguiente en recorrer una distancia de 0 millas:
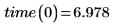
Esto no tiene sentido si el tiempo medido es únicamente el tiempo de viaje a una velocidad constante. A veces, este tipo de resultado indica un fenómeno físico determinado. En este caso, el tiempo necesario para recorrer cero millas se puede interpretar como el tiempo de espera medio en semáforos.
5. Trace los puntos de datos y la línea de trayectoria de ajuste.
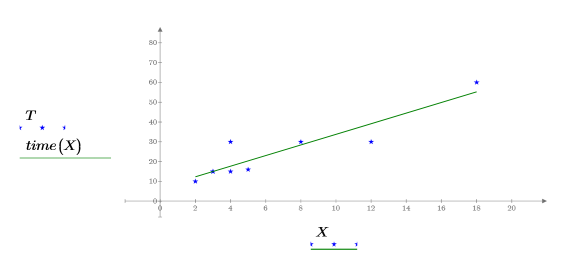
Métodos alternativos para calcular la pendiente y la intercepción
Existen varios métodos para calcular la pendiente y la intercepción para la línea de trayectoria de ajuste. Por ejemplo, la función line combina las funciones slope e intercept. Otros métodos incluyen cálculos de matrices o relaciones estadísticas.
1. Llame a las funciones intercept y slope.
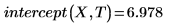
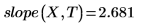
2. Llame a la función line.
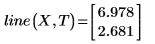
3. Utilice el cálculo de matrices con la función augment.
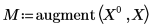
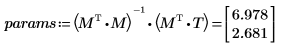
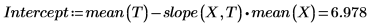
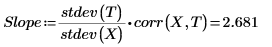
5. Utilice un gráfico para mostrar que la línea de mínimos cuadrados siempre pasa por el punto (mean(X), mean(T)):
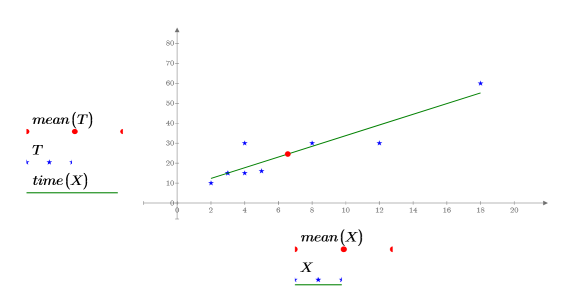
Errores estándar
Calcule el error estándar del cálculo aproximado (también conocido como error estándar) para medir la adecuación del ajuste lineal anterior. Calcule también el error de la pendiente y la intercepción.
1. Defina los grados de libertad de movimiento (el número de puntos de datos menos el número de parámetros ajustados).
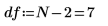
2. Llame a la función stderr para calcular el error estándar del cálculo aproximado para la línea de trayectoria de ajuste definida anteriormente.
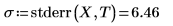
Esta es la raíz cuadrada del error cuadrático medio (MSE) o σ2:
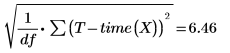
3. Compare el error estándar calculado con el error estándar devuelto por la función polyfitstat.
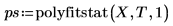
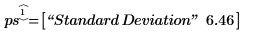
4. Calcule los errores estándar de la pendiente y la intercepción.
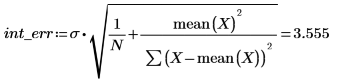
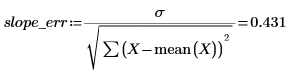
5. Repita el cálculo anterior con el cálculo de matrices.
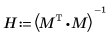
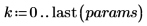
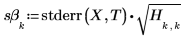
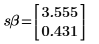
6. Utilice la función augment para mostrar que los errores estándar de cada coeficiente de regresión se graban en la matriz que ha devuelto la función polyfitc.
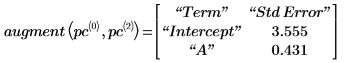
Intervalos de confianza para cada coeficiente
Utilice los cálculos aproximados anteriores, junto con los puntos de percentil de la distribución t de Student, para crear un intervalo de confianza de los cálculos aproximados de la pendiente y la intercepción.
1. Defina el nivel de significancia de un intervalo de confianza del 98% y use la función qt para calcular el factor t.
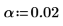
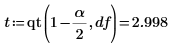
2. Calcule los límites de confianza de la pendiente.
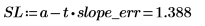
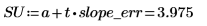
Hay un 98% de posibilidades de que el valor real de la pendiente se encuentre entre SL y SU.
3. Calcule los límites de confianza de la intercepción.
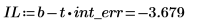
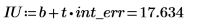
El amplio rango de este valor refleja el elevado nivel de dispersión de los datos.
4. Llame a la función confidence para repetir los pasos del 1 al 3.
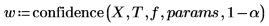
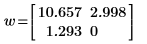
La función confidence devuelve el ancho de los intervalos de confianza en la primera columna y el factor t en la segunda columna. Al dividir los anchos por el factor t, obtendrá los errores estándar de ambos parámetros:
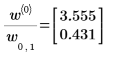
5. Para buscar los límites de confianza, se puede añadir o sustraer el ancho del parámetro pertinente:
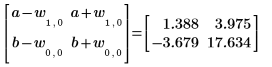
6. Utilice la función augment para mostrar que los errores estándar de cada coeficiente de regresión se graban en la matriz que ha devuelto la función polyfitc.

Intervalos de confianza para la regresión
1. Utilice las funciones length y mean para calcular un intervalo de confianza para la propia regresión.
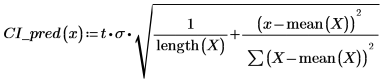
2. Utilice la función anterior para calcular el intervalo de confianza de cualquier valor x previsto:
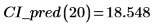
3. Utilice el cálculo de matrices:
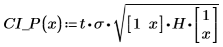
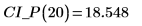
4. Trace los datos, la línea de trayectoria de ajuste y el intervalo de confianza de toda la región de regresión.
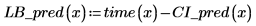
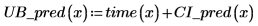
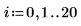
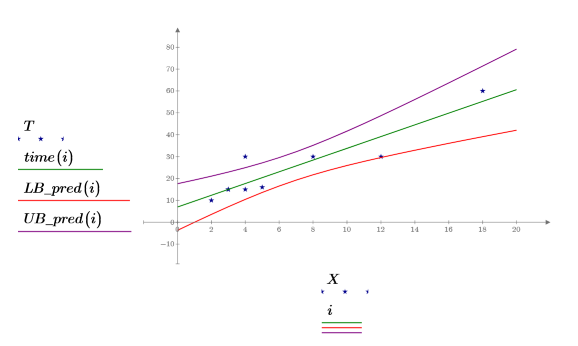
La región de confianza para los valores previstos se estrecha cerca del centro de los valores medidos. Esto se debe a que las fórmulas utilizadas para calcular la regresión se basan en la media, por lo que los valores previstos más cercanos a la media de los datos son más precisos.
5. Calcule los límites de confianza de los valores medidos. Estos límites son ligeramente diferentes de los límites para los valores previstos.
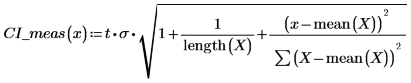
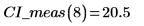
6. Utilice el cálculo de matrices:
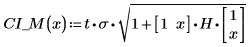
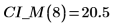
7. Trace los límites de confianza como una traza de error.
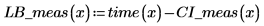
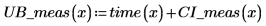
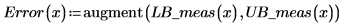
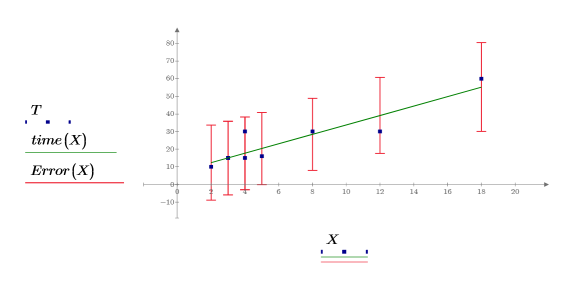
Es posible utilizar los gráficos como una forma de detección de valores atípicos, donde los valores medidos que no se encuentran dentro de los intervalos de confianza indican un valor atípico. |