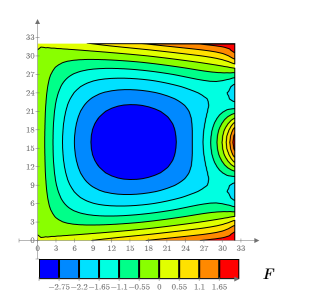
Ejemplo: flujo de calor en una placa cuadrada (II)
Resuelva la distribución de temperatura de estado estable de una placa cuadrada usando el solver de ecuaciones diferenciales parciales relax.
Resolución de la ecuación de Poisson
Resuelva la ecuación de calor cuyos valores de la función de origen son conocidos y las condiciones de límite distintas de cero.
|
|
La función relax se basa en un método de resolución completamente diferente, por lo que requiere un conjunto de argumentos distinto.
|
1. Defina cinco matrices cuadradas a, b, c, d y e destinadas a contener los coeficientes de la aproximación laplaciana:
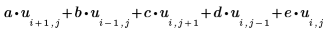
Estos arrays pueden tener cualquier tamaño que especifique el usuario. Cuanto más grande, más fina será la malla de la solución. |
2. Defina la dimensión de la placa cuadrada:
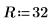
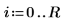
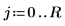
3. Defina los coeficientes:
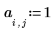
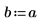
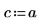
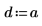
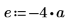
4. Defina la resistencia y la posición de una fuente constante.
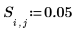
5. Defina una matriz cuadrada f, de tamaño igual al de la rejilla, que contenga los valores de límite conocidos de la función F(x,y) y los valores de prueba de los valores internos desconocidos.
◦ Condición de límite en la parte superior:
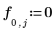
◦ Condición de límite en la parte inferior:
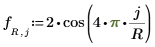
◦ Condición de límite en los bordes:
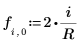
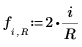
6. Defina la variable r Jacobi spectral radius, un número real entre 0 y 1.
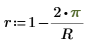
Este parámetro controla la convergencia del algoritmo. Si aparece el mensaje de error que indica que existen "demasiadas iteraciones", inténtelo reduciendo r. |
7. Llame a la función relax:
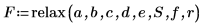
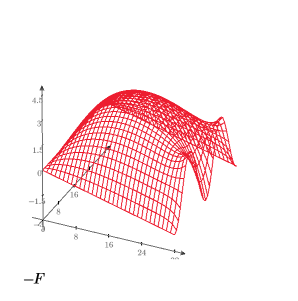
8. Cree un gráfico 3D para mostrar la distribución de calor sobre la placa cuadrada.
9. Cree un gráfico de contorno para mostrar las líneas de temperatura constante.