Ejemplo: oscilación armónica amortiguada en circuitos
Dado un sencillo circuito eléctrico que contiene una resistencia R, un inductor L y un condensador C.
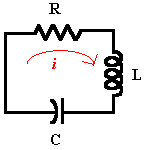
Utilice ecuaciones diferenciales para modelar la carga Q en el condensador C y, a continuación, utilice funciones del solver de EDO para buscar otras soluciones aproximadas. Por último, compare los resultados con la solución exacta de Q.
Uso de ecuaciones diferenciales
1. Escriba una ecuación diferencial para el voltaje mediante los tres componentes que deben sumar cero:
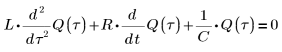
2. Escriba la ecuación diferencial para el cambio instantáneo de la carga Q en el condensador C:
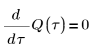
3. Defina la carga Q en el tiempo cero:
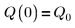
4. Suponga los siguientes valores de los parámetros de entrada:
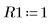
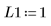
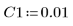
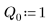
5. Transforme la ecuación diferencial a la forma estándar:
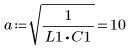
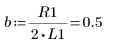
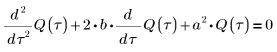
6. Resuelva la ecuación para todos los casos de a y b:
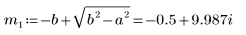
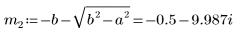
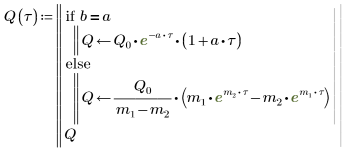
7. Trace las dos posibles soluciones de Q:
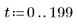
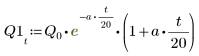
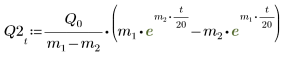
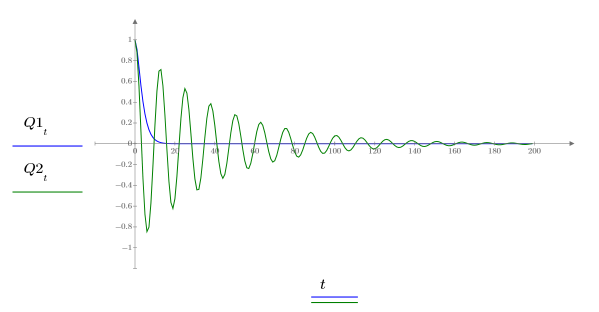
La carga Q1 decrece rápidamente hasta cero cuando a=b y oscila durante mucho tiempo antes de llegar a cero cuando a y b no son iguales.
Antes de utilizar los solvers de EDO
• Defina los parámetros que se van a pasar a las funciones del solver de EDO:
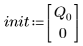 | 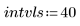 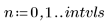 |
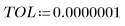 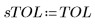 | 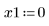 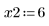 |
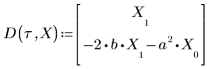 |
• Los solvers de EDO se dividen en dos tipos: solver para sistemas stiff y solver para sistemas no stiff. Un sistema de EDO escrito en forma matricial como y' = Ax se denomina stiff si la matriz A es casi singular. En caso contrario, el sistema es no stiff.
• La distinción entre los sistemas stiff y no stiff puede estar relacionada con las escalas dinámicas inherentes de la matriz A según esté caracterizada por sus autovalores. Una matriz con autovalores dispares (o valores que van desde muy pequeños hasta muy grandes) generalmente será un sistema stiff.
• A partir de los parámetros especificados del sistema, este ejemplo armónico amortiguado sencillo representa un sistema no stiff.
• Las funciones Adams, AdamsBDF, BDF y Radau pueden recibir un valor específico de TOL o usar su propio valor TOL por defecto de 10-5.
Uso de los solvers de EDO para sistemas no stiff
Utilice los solvers de EDO para sistemas no stiff para buscar las soluciones aproximadas y, a continuación, comparar los resultados con la solución exacta de Q.
1. Adams
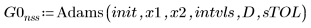
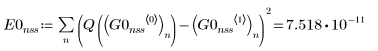
2. rkfixed
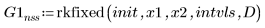
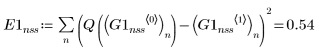
3. Rkadapt
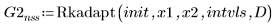
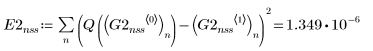
4. Bulstoer
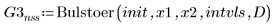

Uso de los solvers de EDO para sistemas stiff
Utilice los solvers de EDO para sistemas stiff para buscar las soluciones aproximadas y, a continuación, comparar los resultados con la solución exacta de Q.
1. BDF
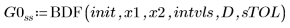
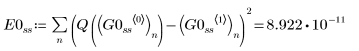
2. Radau
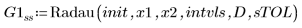
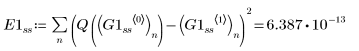
Uso de un solver híbrido de EDO
Utilice el solver híbrido de EDO AdamsBDF, que determina si un sistema es stiff o no stiff y llama a Adams o BDF según corresponda, para encontrar las soluciones aproximadas; a continuación, compare los resultados con la solución exacta de Q.
1. AdamsBDF
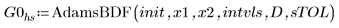
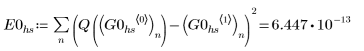
Conclusión
• En los solvers de EDO para sistemas no stiff, las funciones Adams y rkfixed devuelven las soluciones con el error más pequeño y más grande, respectivamente.
• En los solvers de EDO para sistemas stiff, las funciones Radau y BDF devuelven las soluciones con el error más pequeño y más grande, respectivamente.
• La función híbrida AdamsBDF devuelve un valor que es más pequeño que ambos valores devueltos por Adams o BDF.
• Globalmente, las funciones Radau y rkfixed devuelven las soluciones con el error más pequeño y más grande, respectivamente.
Comparación de resultados
1. Trace las soluciones devueltas por los solvers de EDO para sistemas no stiff con los errores más pequeño (Adams, G0nss) y más grande (rkfixed, G1nss):
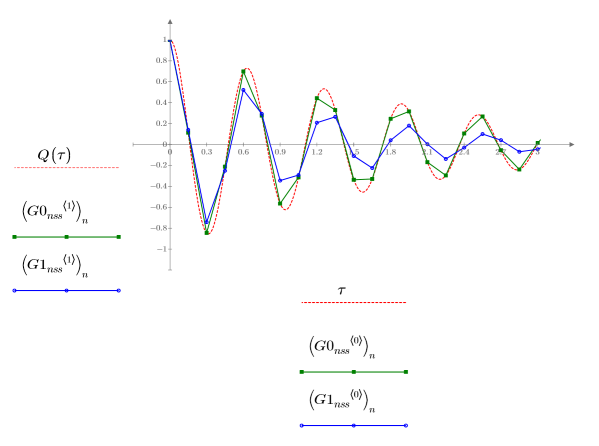
Existe una diferencia patente entre las dos soluciones devueltas en relación con Q.
2. Trace las soluciones devueltas por los solvers de EDO para los sistemas stiff con los errores más pequeño (Radau, G1ss) y más grande (BDF, G0ss):
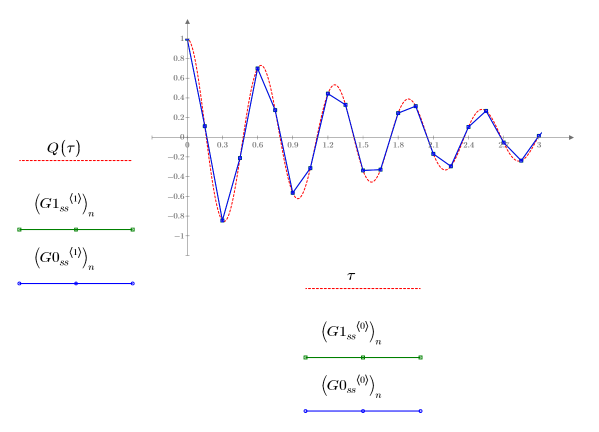
Las dos soluciones parecen idénticas con respecto a Q.
3. Trace las soluciones que han producido los errores más pequeños (Radau, G1ss) y más grandes (rkfixed, G1nss), devueltas por los solvers de EDO para sistemas stiff y no stiff:
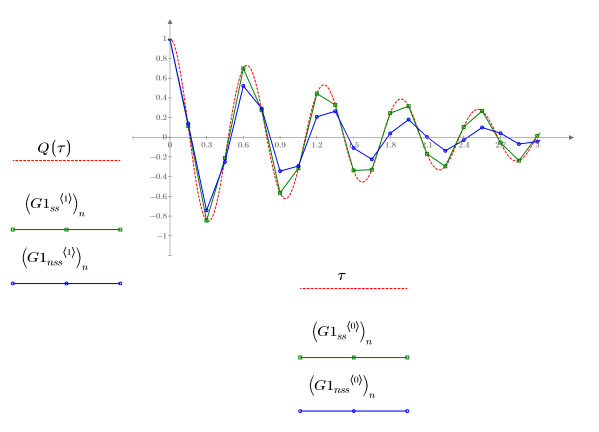
La función Radau, un solver de sistema stiff, devuelve la mejor aproximación a la solución de Q.